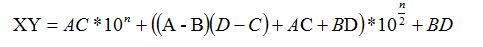大整数乘法（分治法）

题目描述：设X和Y都是n位的十进制整数，计算它们的乘积X*Y。

如果按照我们日常的计算方法，应该就是将两个数逐位相乘，最后加起来得到最终的结果，时间复杂度为O（n²）;

因此我们思考，能不能采用分治法来降低时间复杂度。

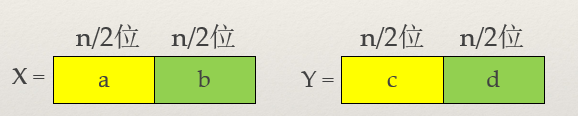
我们将X和Y按照上述方式划分，故可得：

**XY = ac×10ⁿ + (ad + bc)×10^n/2 + bd； **

但是经过分析可以看出，这样处理并没有降低时间复杂度，那么我们是否可以减少乘法计算来降低O？

XY = ac×10ⁿ + ((a-b)(d-c) + ac + bd)×10^n/2 + bd

XY = ac×10ⁿ + ((a+b)(d+c) - ac - bd)×10^n/2 + bd

这样以来我们只需要计算三次乘法即可。

但是需要注意一点，事实上因为 n/2为 floor除法，故而 n的奇偶性会导致结果出错，下面附上数学分析：
$$\begin{gathered} n/2=[n/2] \\ X=a\times 10^{[n/2]}+B \\ Y=b\times 10^{[n/2]}+C \\ XY=ab\times 10^{2\times [n/2]}+((a+b)(c+d)-ac-bd)\times 10^{[n/2]}+bd \end{gathered}$$

从上述计算中可以看出，如果n为偶数时，关系计算是正确的；

但是当n为奇数时，因为高斯取整的性质，需要对XY的结果做出改变：
$$XY=ab\times 10^{2\times [n/2]-1}+((a+b)(c+d)-ac-bd)\times 10^{[n/2]}+bd$$
下面附上具体代码部分：

import java.util.Scanner;public class Study {//相同长度的非负大整数乘法public static void main(String[] args) {Scanner in = new Scanner(System.in);long X = in.nextLong();long Y = in.nextLong();//定义并初始化两个大整数int length = in.nextInt();long answer = multiplyNum(X, Y, length);System.out.println(answer);}public static long multiplyNum(long X, long Y, int n) {if (X == 0 || Y == 0) return 0;//其中某一整数为零if (n == 1) return X * Y;//如果达到了可计算的标准(不一定为一位)int length = n / 2;//位数划分long A = X / (int) (Math.pow(10, length));long B = X % (int) (Math.pow(10, length));long C = Y / (int) (Math.pow(10, length));long D = Y % (int) (Math.pow(10, length));//拆分整数long AC = multiplyNum(A, C, length);long BD = multiplyNum(B, D, length);//继续拆分long E = multiplyNum(A + B, C + D, length);if (n % 2 == 0) return AC * (long) (Math.pow(10, n)) + BD + (E - AC - BD) * (long) (Math.pow(10, length));else return AC * (long) (Math.pow(10, n - 1)) + BD + (E - AC - BD) * (long) (Math.pow(10, length));}
}