12种降维方法终极指南（含Python代码）

你遇到过特征超过1000个的数据集吗？超过5万个的呢？我遇到过。降维是一个非常具有挑战性的任务，尤其是当你不知道该从哪里开始的时候。拥有这么多变量既是一个恩惠——数据量越大，分析结果越可信；也是一种诅咒——你真的会感到一片茫然，无从下手。

面对这么多特征，在微观层面分析每个变量显然不可行，因为这至少要几天甚至几个月，而这背后的时间成本是难以估计的。为此，我们需要一种更好的方法来处理高维数据，比如本文介绍的降维：一种能在减少数据集中特征数量的同时，避免丢失太多信息并保持/改进模型性能的方法。

什么是降维？

每天，我们都会生成大量数据，而事实上，现在世界上约90%的数据都是在过去3到4年中产生的，这是个令人难以置信的现实。下面是收集数据的几个示例：

• Facebook会收集你喜欢、分享、发布、访问的内容等数据，比如你喜欢哪家餐厅。
• 智能手机中的各类应用会收集大量关于你的个人信息，比如你所在的地点。
• 淘宝会收集你在其网站上购买、查看、点击的内容等数据。
• 赌场会跟踪每位客户的每一步行动。

随着数据的生成和数据收集量的不断增加，可视化和绘制推理图变得越来越困难。一般情况下，我们经常会通过绘制图表来可视化数据，比如假设我们手头有两个变量，一个年龄，一个身高。我们就可以绘制散点图或折线图，轻松反映它们之间的关系。

下图是一个简单的例子：

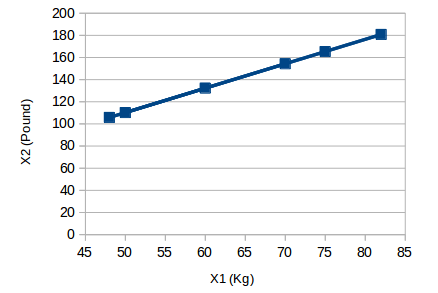
横坐标X1的单位为“千克”，纵坐标X2的单位为“磅”。可以发现，虽然是两个变量，但它们传达的信息是一致的，即物体的重量。所以我们只需选用其中的一个就能保留原始意义，把2维数据压缩到1维（Y1）后，上图就变成：

类似地，我们可以把数据从原本的p维转变为一系列k维的子集（k<<n），这就是降维。

为什么要降维？

以下是在数据集中应用降维的用处：

• 随着数据维度不断降低，数据存储所需的空间也会随之减少。
• 低维数据有助于减少计算/训练用时。
• 一些算法在高维度数据上容易表现不佳，降维可提高算法可用性。
• 降维可以用删除冗余特征解决多重共线性问题。比如我们有两个变量：“一段时间内在跑步机上的耗时”和“卡路里消耗量”。这两个变量高度相关，在跑步机上花的时间越长，燃烧的卡路里自然就越多。因此，同时存储这两个数据意义不大，只需一个就够了。
• 降维有助于数据可视化。如前所述，如果数据维度很高，可视化会变得相当困难，而绘制二维三维数据的图表非常简单。

数据集1：Big Mart Sales III

降维技术一览

数据维度的降低方法主要有两种：

• 仅保留原始数据集中最相关的变量（特征选择）。
• 寻找一组较小的新变量，其中每个变量都是输入变量的组合，包含与输入变量基本相同的信息（降维）。

1. 缺失值比率（Missing Value Ratio）

假设你有一个数据集，你第一步会做什么？在构建模型前，对数据进行探索性分析必不可少。但在浏览数据的过程中，有时候我们会发现其中包含不少缺失值。如果缺失值少，我们可以填补缺失值或直接删除这个变量；如果缺失值过多，你会怎么办呢？

当缺失值在数据集中的占比过高时，一般我会选择直接删除这个变量，因为它包含的信息太少了。但具体删不删、怎么删需要视情况而定，我们可以设置一个阈值，如果缺失值占比高于阈值，删除它所在的列。阈值越高，降维方法越积极。

下面是具体代码：

# 导入需要的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

加载数据：

# 读取数据
train=pd.read_csv("Train_UWu5bXk.csv")

[注]：应在读取数据时添加文件的路径。

用.isnull().sum()检查每个变量中缺失值的占比：

train.isnull().sum()/len(train)*100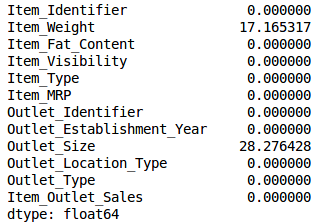

如上表所示，缺失值很少。我们设阈值为20%：

# 保存变量中的缺失值
a = train.isnull().sum()/len(train)*100
# 保存列名
variables = train.columns
variable = [ ]
for i in range(0,12):if a[i]<=20:   #setting the threshold as 20%variable.append(variables[i])

2. 低方差滤波（Low Variance Filter）

如果我们有一个数据集，其中某列的数值基本一致，也就是它的方差非常低，那么这个变量还有价值吗？和上一种方法的思路一致，我们通常认为低方差变量携带的信息量也很少，所以可以把它直接删除。

放到实践中，就是先计算所有变量的方差大小，然后删去其中最小的几个。需要注意的一点是：方差与数据范围相关的，因此在采用该方法前需要对数据做归一化处理。

放在示例中，我们先估算缺失值：

train['Item_Weight'].fillna(train['Item_Weight'].median, inplace=True)
train['Outlet_Size'].fillna(train['Outlet_Size'].mode()[0], inplace=True)

检查缺失值是否已经被填充：

train.isnull().sum()/len(train)*100

再计算所有数值变量的方差：

train.var()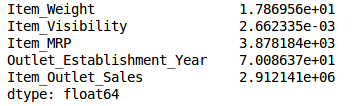

如上图所示，和其他变量相比，Item_Visibility的方差非常小，因此可以把它直接删除。

umeric = train[['Item_Weight', 'Item_Visibility', 'Item_MRP', 'Outlet_Establishment_Year']]
var = numeric.var()
numeric = numeric.columns
variable = [ ]
for i in range(0,len(var)):if var[i]>=10:   # 将阈值设置为10％variable.append(numeric[i+1])

以上代码帮我们列出了方差大于10的所有变量。

3. 高相关滤波（High Correlation filter）

如果两个变量之间是高度相关的，这意味着它们具有相似的趋势并且可能携带类似的信息。同理，这类变量的存在会降低某些模型的性能（例如线性和逻辑回归模型）。为了解决这个问题，我们可以计算独立数值变量之间的相关性。如果相关系数超过某个阈值，就删除其中一个变量。

作为一般准则，我们应该保留那些与目标变量显示相当或高相关性的变量。

首先，删除因变量（Item_Outlet_Sales），并将剩余的变量保存在新的数据列（df）中。

df=train.drop('Item_Outlet_Sales', 1)
df.corr()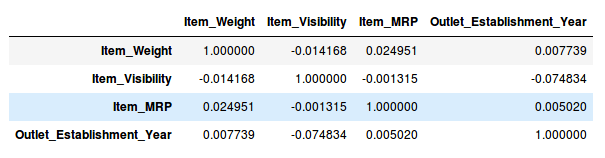

如上表所示，示例数据集中不存在高相关变量，但通常情况下，如果一对变量之间的相关性大于0.5-0.6，那就应该考虑是否要删除一列了。

4. 随机森林（Random Forest）

随机森林是一种广泛使用的特征选择算法，它会自动计算各个特征的重要性，所以无需单独编程。这有助于我们选择较小的特征子集。

在开始降维前，我们先把数据转换成数字格式，因为随机森林只接受数字输入。同时，ID这个变量虽然是数字，但它目前并不重要，所以可以删去。

from sklearn.ensemble import RandomForestRegressor
df=df.drop(['Item_Identifier', 'Outlet_Identifier'], axis=1)
model = RandomForestRegressor(random_state=1, max_depth=10)
df=pd.get_dummies(df)
model.fit(df,train.Item_Outlet_Sales)

拟合模型后，根据特征的重要性绘制成图：

features = df.columns
importances = model.feature_importances_
indices = np.argsort(importances[0:9])  # top 10 features
plt.title('Feature Importances')
plt.barh(range(len(indices)), importances[indices], color='b', align='center')
plt.yticks(range(len(indices)), [features[i] for i in indices])
plt.xlabel('Relative Importance')
plt.show()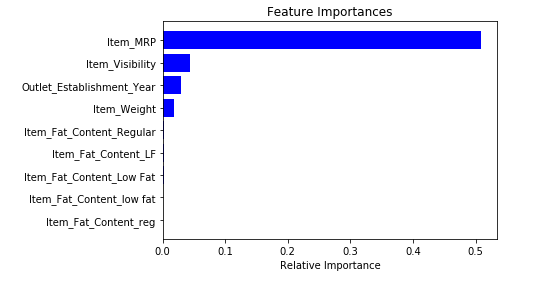

基于上图，我们可以手动选择最顶层的特征来减少数据集中的维度。如果你用的是sklearn，可以直接使用SelectFromModel，它根据权重的重要性选择特征。

from sklearn.feature_selection import SelectFromModel
feature = SelectFromModel(model)
Fit = feature.fit_transform(df, train.Item_Outlet_Sales)

5. 反向特征消除（Backward Feature Elimination）

以下是反向特征消除的主要步骤：

• 先获取数据集中的全部n个变量，然后用它们训练一个模型。
• 计算模型的性能。
• 在删除每个变量（n次）后计算模型的性能，即我们每次都去掉一个变量，用剩余的n-1个变量训练模型。
• 确定对模型性能影响最小的变量，把它删除。
• 重复此过程，直到不再能删除任何变量。

在构建线性回归或Logistic回归模型时，可以使用这种方法。

from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import RFE
from sklearn import datasets
lreg = LinearRegression()
rfe = RFE(lreg, 10)
rfe = rfe.fit_transform(df, train.Item_Outlet_Sales)

我们需要指定算法和要选择的特征数量，然后返回反向特征消除输出的变量列表。此外，rfe.ranking_可以用来检查变量排名。

6. 前向特征选择（Forward Feature Selection）

前向特征选择其实就是反向特征消除的相反过程，即找到能改善模型性能的最佳特征，而不是删除弱影响特征。它背后的思路如下所述：

• 选择一个特征，用每个特征训练模型n次，得到n个模型。
• 选择模型性能最佳的变量作为初始变量。
• 每次添加一个变量继续训练，重复上一过程，最后保留性能提升最大的变量。
• 一直添加，一直筛选，直到模型性能不再有明显提高。

from sklearn.feature_selection import f_regression
ffs = f_regression(df,train.Item_Outlet_Sales )

上述代码会返回一个数组，其中包括变量F值和每个F对应的p值（什么是F值）。在这里，我们选择F值大于10的变量：

variable = [ ]
for i in range(0,len(df.columns)-1):if ffs[0][i] >=10:variable.append(df.columns[i])

[注]：前向特征选择和反向特征消除耗时较久，计算成本也都很高，所以只适用于输入变量较少的数据集。

到目前为止，我们介绍的6种方法都能很好地解决示例的商场销售预测问题，因为这个数据集本身输入变量不多。在下文中，为了展示多变量数据集的降维方法，我们将把数据集改成Fashion MNIST，它共有70,000张图像，其中训练集60,000张，测试集10,000张。我们的目标是训练一个能分类各类服装配饰的模型。

数据集2：Fashion MNIST

7. 因子分析（Factor Analysis）

因子分析是一种常见的统计方法，它能从多个变量中提取共性因子，并得到最优解。假设我们有两个变量：收入和教育。它们可能是高度相关的，因为总体来看，学历高的人一般收入也更高，反之亦然。所以它们可能存在一个潜在的共性因子，比如“能力”。

在因子分析中，我们将变量按其相关性分组，即特定组内所有变量的相关性较高，组间变量的相关性较低。我们把每个组称为一个因子，它是多个变量的组合。和原始数据集的变量相比，这些因子在数量上更少，但携带的信息基本一致。

import pandas as pd
import numpy as np
from glob import glob
import cv2
images = [cv2.imread(file) for file in glob('train/*.png')]

[注]：你必须使用train文件夹的路径替换glob函数内的路径。

现在我们先把这些图像转换为numpy数组格式，以便执行数学运算并绘制图像。

images = np.array(images)
images.shape

返回：(60000, 28, 28, 3)

如上所示，这是一个三维数组，但我们的目标是把它转成一维，因为后续只接受一维输入。所以我们还得展平图像：

image = []
for i in range(0,60000):img = images[i].flatten()image.append(img)
image = np.array(image)

创建一个数据框，其中包含每个像素的像素值，以及它们对应的标签：

train = pd.read_csv("train.csv")     # Give the complete path of your train.csv file
feat_cols = [ 'pixel'+str(i) for i in range(image.shape[1]) ]
df = pd.DataFrame(image,columns=feat_cols)
df['label'] = train['label']

用因子分析分解数据集：

from sklearn.decomposition import FactorAnalysis
FA = FactorAnalysis(n_components = 3).fit_transform(df[feat_cols].values)

这里，n_components将决定转换数据中的因子数量。转换完成后，可视化结果：

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(12,8))
plt.title('Factor Analysis Components')
plt.scatter(FA[:,0], FA[:,1])
plt.scatter(FA[:,1], FA[:,2])
plt.scatter(FA[:,2],FA[:,0])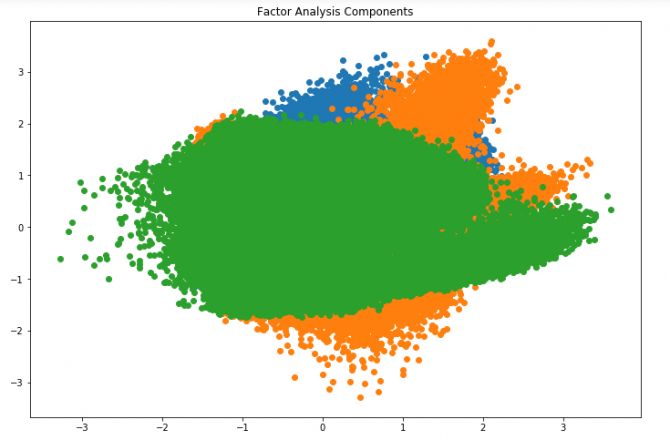

在上图中，x轴和y轴表示分解因子的值，虽然共性因子是潜在的，很难被观察到，但我们已经成功降维。

8. 主成分分析（PCA）

如果说因子分析是假设存在一系列潜在因子，能反映变量携带的信息，那PCA就是通过正交变换将原始的n维数据集变换到一个新的被称做主成分的数据集中，即从现有的大量变量中提取一组新的变量。下面是关于PCA的一些要点：

• 主成分是原始变量的线性组合。
• 第一个主成分具有最大的方差值。
• 第二主成分试图解释数据集中的剩余方差，并且与第一主成分不相关（正交）。
• 第三主成分试图解释前两个主成分等没有解释的方差。

再进一步降维前，我们先随机绘制数据集中的某些图：

rndperm = np.random.permutation(df.shape[0])
plt.gray()
fig = plt.figure(figsize=(20,10))
for i in range(0,15):ax = fig.add_subplot(3,5,i+1)ax.matshow(df.loc[rndperm[i],feat_cols].values.reshape((28,28*3)).astype(float))

实现PCA：

from sklearn.decomposition import PCA
pca = PCA(n_components=4)
pca_result = pca.fit_transform(df[feat_cols].values)

其中n_components将决定转换数据中的主成分。接下来，我们看一下这四个主成分解释了多少方差：

plt.plot(range(4), pca.explained_variance_ratio_)
plt.plot(range(4), np.cumsum(pca.explained_variance_ratio_))
plt.title("Component-wise and Cumulative Explained Variance")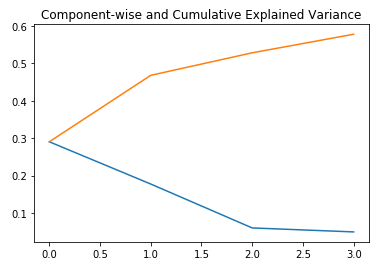

在上图中，蓝线表示分量解释的方差，而橙线表示累积解释的方差。我们只用四个成分就解释了数据集中约60％的方差。

9. 独立分量分析（ICA）

独立分量分析（ICA）基于信息理论，是最广泛使用的降维技术之一。PCA和ICA之间的主要区别在于，PCA寻找不相关的因素，而ICA寻找独立因素。

如果两个变量不相关，它们之间就没有线性关系。如果它们是独立的，它们就不依赖于其他变量。例如，一个人的年龄和他吃了什么/看了什么电视无关。

该算法假设给定变量是一些未知潜在变量的线性混合。它还假设这些潜在变量是相互独立的，即它们不依赖于其他变量，因此它们被称为观察数据的独立分量。

下图是ICA和PCA的一个直观比较：

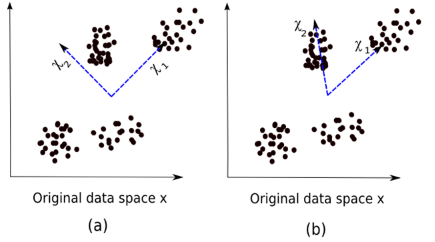
(a)PCA，(b)ICA

PCA的等式是x = Wχ。

这里，

• x是观察结果
• W是混合矩阵
• χ是来源或独立分量

现在我们必须找到一个非混合矩阵，使分量尽可能独立。而测试分量独立性最常用的方法是非高斯性：

• 根据中心极限定理（Central Limit Theorem），多个独立随机变量混合之后会趋向于正态分布（高斯分布）。

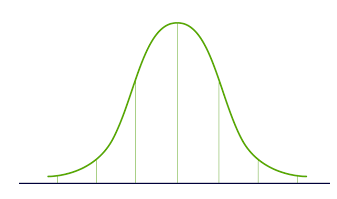
• 因此，我们可以寻找所有独立分量中能最大化峰度的分量。
• 一旦峰度被最大化，整个分布会呈现非高斯分布，我们也能得到独立分量。

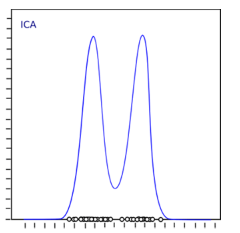
在Python中实现ICA：

from sklearn.decomposition import FastICA 
ICA = FastICA(n_components=3, random_state=12) 
X=ICA.fit_transform(df[feat_cols].values)

10. IOSMAP

代码：

from sklearn import manifold 
trans_data = manifold.Isomap(n_neighbors=5, n_components=3, n_jobs=-1).fit_transform(df[feat_cols][:6000].values)

使用的参数：

• n_neighbors：决定每个点的相邻点数
• n_components：决定流形的坐标数
• n_jobs = -1：使用所有可用的CPU核心

可视化：

plt.figure(figsize=(12,8))
plt.title('Decomposition using ISOMAP')
plt.scatter(trans_data[:,0], trans_data[:,1])
plt.scatter(trans_data[:,1], trans_data[:,2])
plt.scatter(trans_data[:,2], trans_data[:,0])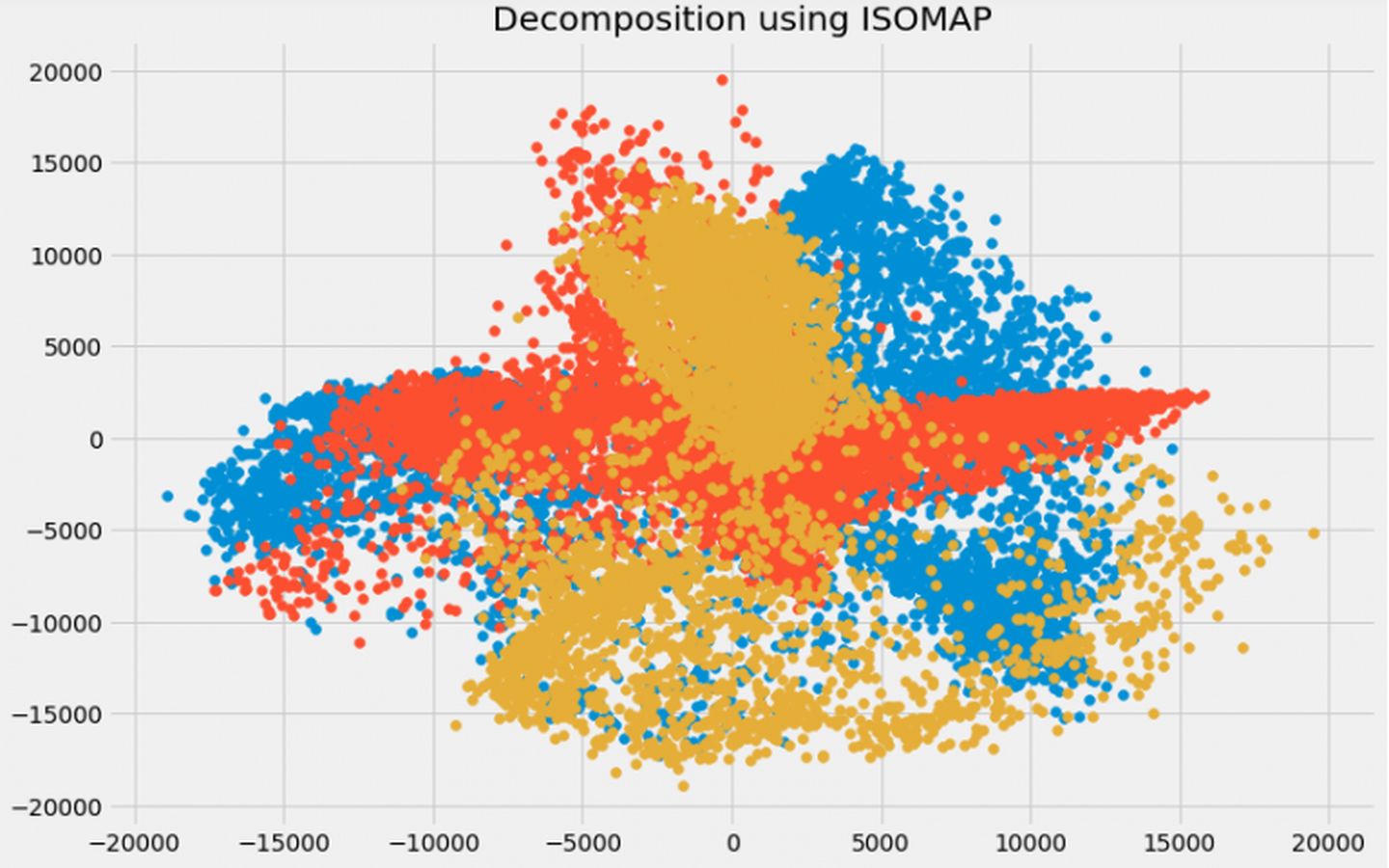

11. t-SNE

代码：

from sklearn.manifold import TSNE 
tsne = TSNE(n_components=3, n_iter=300).fit_transform(df[feat_cols][:6000].values)

可视化：

plt.figure(figsize=(12,8))
plt.title('t-SNE components')
plt.scatter(tsne[:,0], tsne[:,1])
plt.scatter(tsne[:,1], tsne[:,2])
plt.scatter(tsne[:,2], tsne[:,0])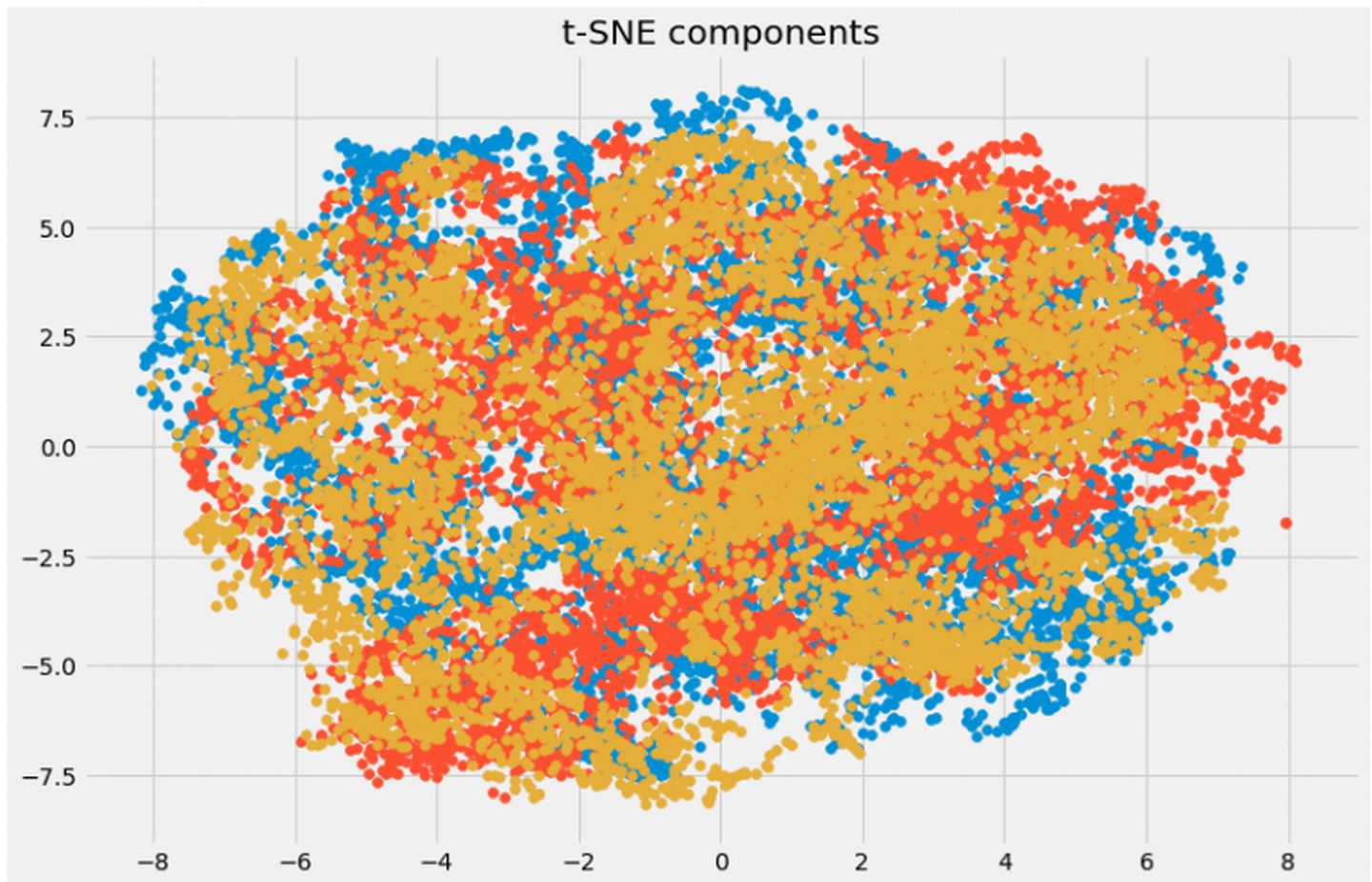

12. UMAP

代码：

import umap
umap_data = umap.UMAP(n_neighbors=5, min_dist=0.3, n_components=3).fit_transform(df[feat_cols][:6000].values)

这里，

• n_neighbors：确定相邻点的数量。
• min_dist：控制允许嵌入的紧密程度，较大的值可确保嵌入点的分布更均匀。

可视化：

plt.figure(figsize=(12,8))
plt.title('Decomposition using UMAP')
plt.scatter(umap_data[:,0], umap_data[:,1])
plt.scatter(umap_data[:,1], umap_data[:,2])
plt.scatter(umap_data[:,2], umap_data[:,0])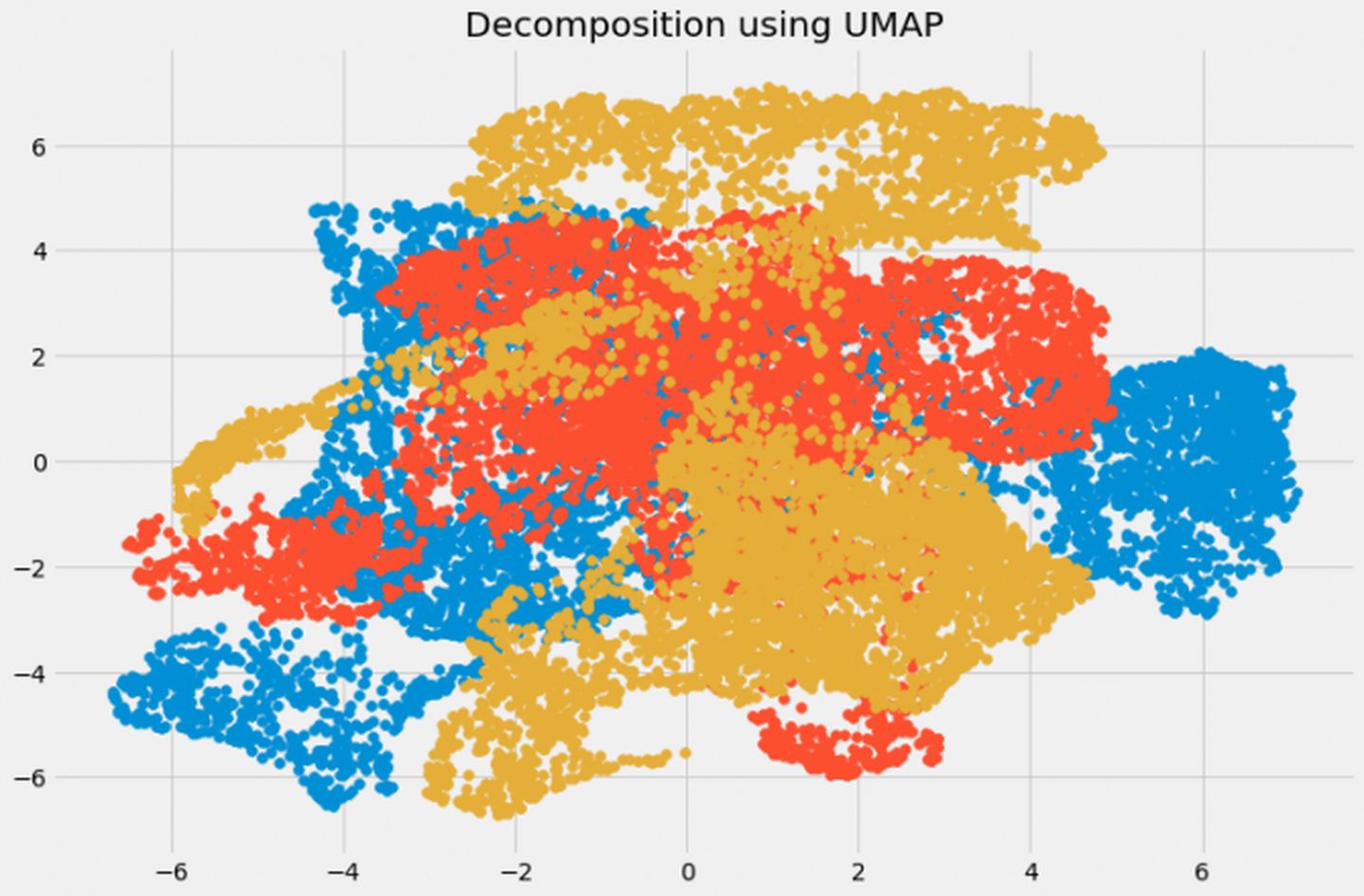

总结

到目前为止，我们已经介绍了12种降维/特征选择方法，考虑到篇幅，我们没有仔细编译后三种方法的原理，感兴趣的读者可以找资料查阅，因为它们中的任何一个都足够写一篇专门介绍的长文。本节会对这12种方法做一个总结，简要介绍它们的优点和缺点。

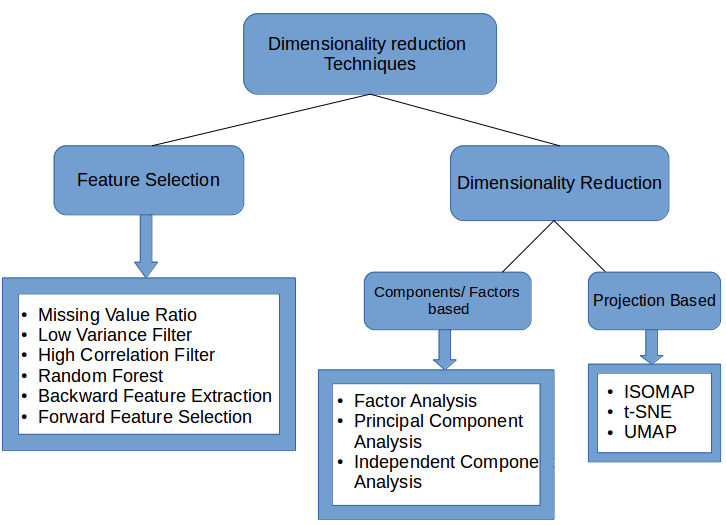
• 缺失值比率：如果数据集的缺失值太多，我们可以用这种方法减少变量数。
• 低方差滤波：这个方法可以从数据集中识别和删除常量变量，方差小的变量对目标变量影响不大，所以可以放心删去。
• 高相关滤波：具有高相关性的一对变量会增加数据集中的多重共线性，所以用这种方法删去其中一个是有必要的。
• 随机森林：这是最常用的降维方法之一，它会明确算出数据集中每个特征的重要性。
• 前向特征选择和反向特征消除：这两种方法耗时较久，计算成本也都很高，所以只适用于输入变量较少的数据集。
• 因子分析：这种方法适合数据集中存在高度相关的变量集的情况。
• PCA：这是处理线性数据最广泛使用的技术之一。
• ICA：我们可以用ICA将数据转换为独立的分量，使用更少的分量来描述数据。
• ISOMAP：适合非线性数据处理。
• t-SNE：也适合非线性数据处理，相较上一种方法，这种方法的可视化更直接。
• UMAP：适用于高维数据，与t-SNE相比，这种方法速度更快。