DES对称加密及三重DES（3DES）

article/2025/9/16 16:31:15

一、DES

1 概述

DES算法全称为Data Encryption Standard，即数据加密算法，它是IBM公司于1975年研究成功并公开发表的。DES算法的入口参数有三个：Key、Data、Mode。其中Key为8个字节共64位，是DES算法的工作密钥；Data也为8个字节64位，是要被加密或被解密的数据；Mode为DES的工作方式,有两种：加密或解密。

2 算法原理

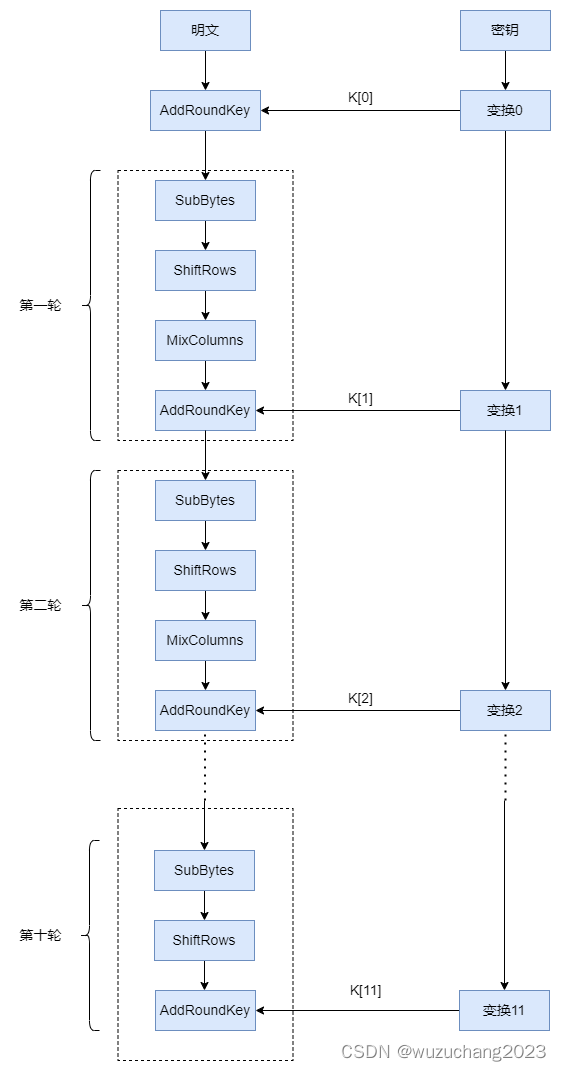
DES算法把64位的明文输入块变为64位的密文输出块，它所使用的密钥也是64位，其算法主要分为两步：

（1）初始置换

其功能是把输入的64位数据块按位重新组合,并把输出分为L0、R0两部分，每部分各长32位，其置换规则为将输入的第58位换到第一位，第50位换到第2位……依此类推,最后一位是原来的第7位。L0、R0则是换位输出后的两部分，L0是输出的左32位，R0是右32位，例：设置换前的输入值为D1D2D3……D64，则经过初始置换后的结果为:L0=D58D50……D8；R0=D57D49……D7。

（2）逆置换

经过16次迭代运算后，得到L16、R16,将此作为输入，进行逆置换，逆置换正好是初始置换的逆运算，由此即得到密文输出。

二、 两个密钥的三重DES

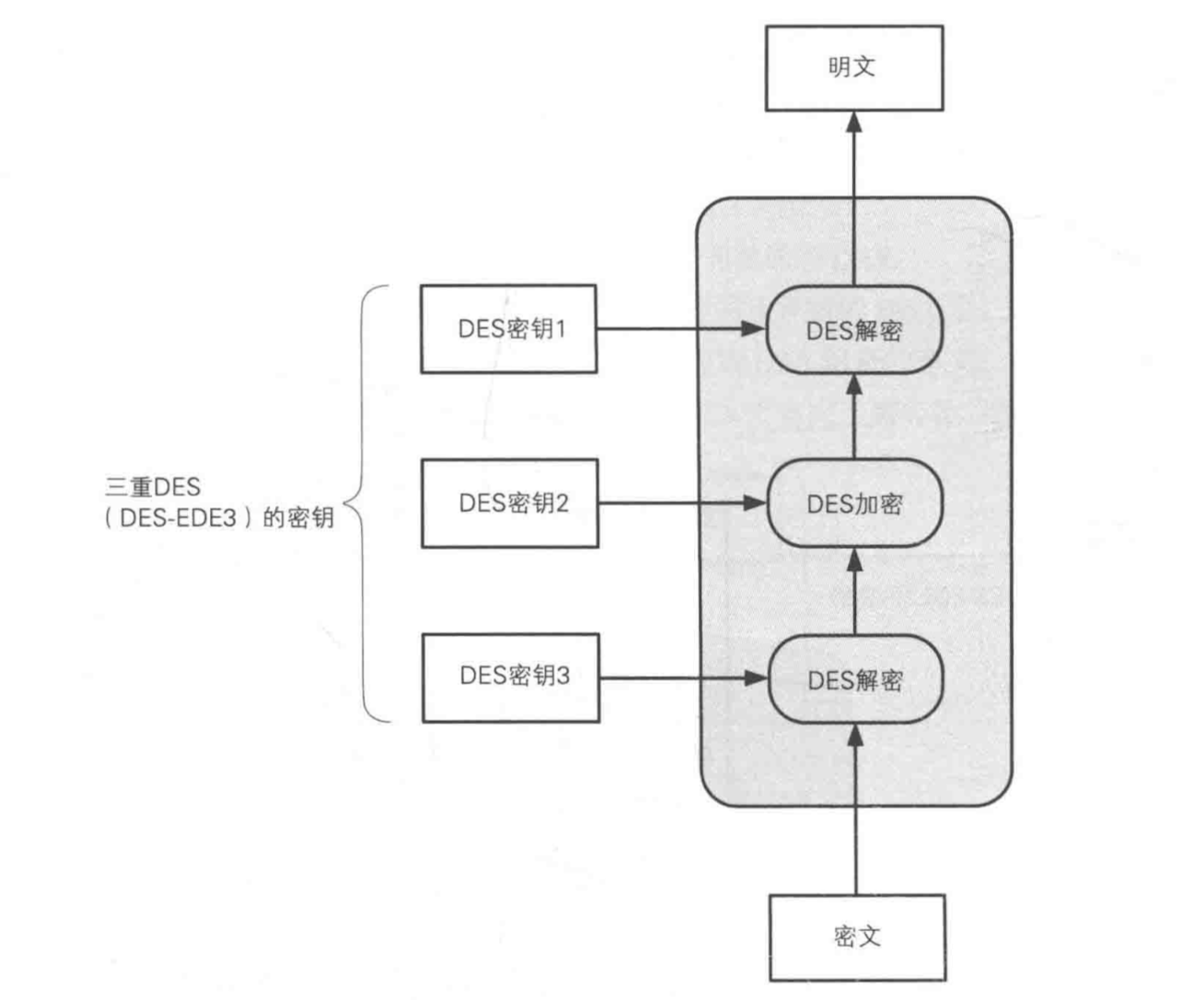
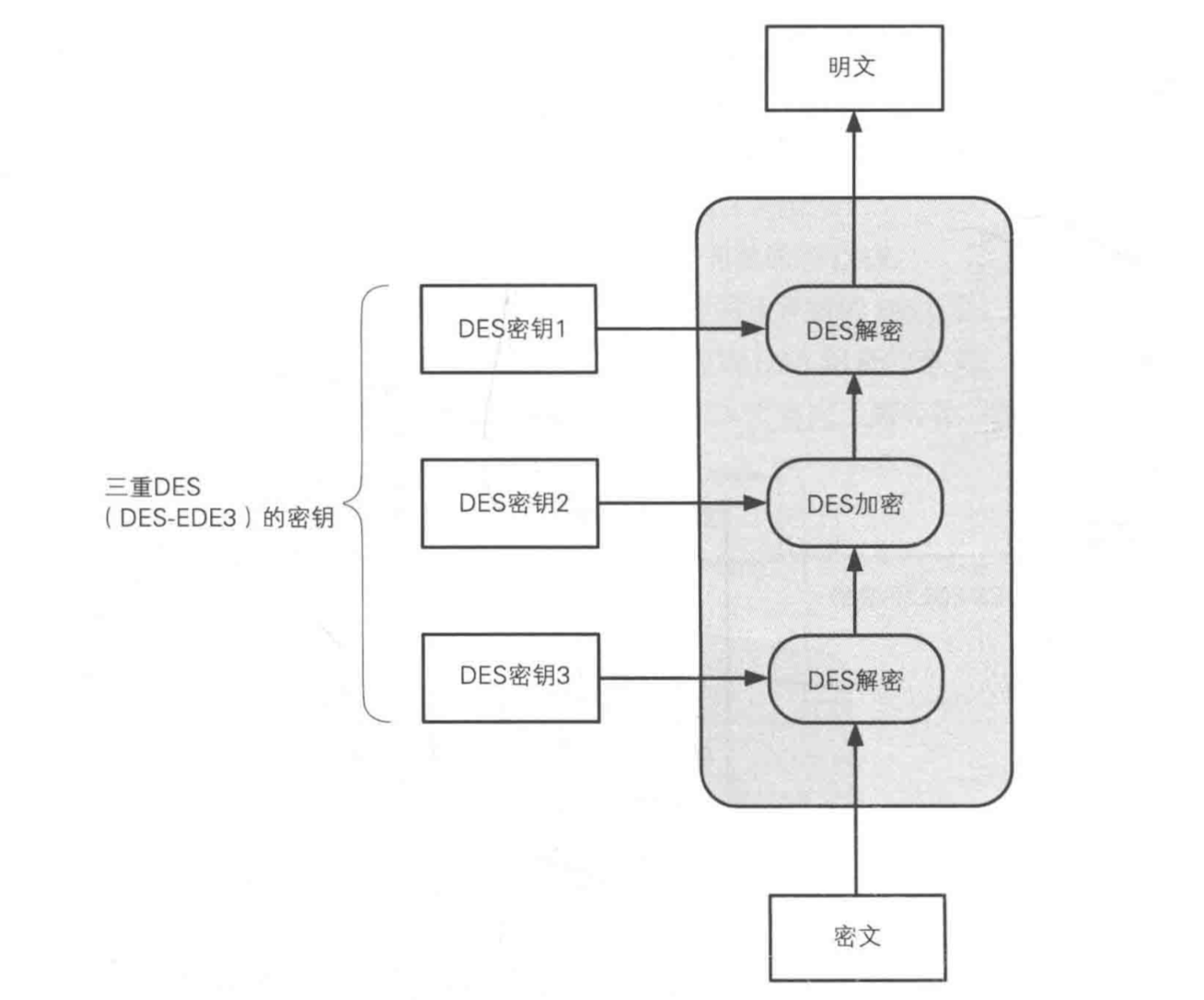
由于DES密钥只有56bit，易于遭受穷举时攻击。作为一种替代加密方案，Tuchman提出使用两个密钥的三重DES加密方法，并在1985年成为美国的一个商用加密标准。该方法使用两个密钥，执行三次DES算法，如图2所示。加密的过程是加密-解密-加密，解密的过程是解密-加密-解密。

采用两个密钥进行三重加密的好处有：①两个密钥合起来有效密钥长度有112bit，可以满足商业应用的需要，若采用总长为168bit的三个密钥，会产生不必要的开销。②加密时采用加密-解密-加密，而不是加密-加密-加密的形式，这样有效的实现了与现有DES系统的向后兼容问题。因为当K1=K2时，三重DES的效果就和原来的DES一样，有助于逐渐推广三重DES。③三重DES具有足够的安全性，目前还没有关于攻破三重DES的报道。

 什么是三重DES

三重DES是为了增加DES的强度，将DES重复3次所得到的一种密码算法，通常缩写为3DES。

二 三重DSE加密

明文经过三次DES处理才能变成最后的密文，由于DES密钥长度实质是56位，因此3DES的密钥长度就是56*3=168比特。

注意：三重DES的三次DES加密是（加密->解密->加密），而不是（加密->加密->加密）,为什么这样设计呢？看看下面这张图就明白了。

如果三次DES加密的密钥都相同，前两次DES，相当于还原成了密文，这样看来，真正起作用的只是最后一次。这样做的好处是：三重DES对DES具备向下兼容性。

还有一种密码叫DES-EDE2,下面我们用图来描述这一种密码。

当然，只有三个密钥互不相等才是正宗的DES-EDE3。

三 三重DES解密

三重DES的解密过程和加密过程正好相反，是以密钥3、密钥2、密钥1的顺序执行解密->加密->解密的操作。

四 三重DES现状

尽管三重DES目前还被银行等机构使用，但其处理速度不高，除了特别重视向下兼容性的情况外，很少被用于新的用途。

pydes:
 

#-*- coding: utf8 -*-#Initial permut matrix for the datas
# IP initial permut
PI = [58, 50, 42, 34, 26, 18, 10, 2,60, 52, 44, 36, 28, 20, 12, 4,62, 54, 46, 38, 30, 22, 14, 6,64, 56, 48, 40, 32, 24, 16, 8,57, 49, 41, 33, 25, 17, 9, 1,59, 51, 43, 35, 27, 19, 11, 3,61, 53, 45, 37, 29, 21, 13, 5,63, 55, 47, 39, 31, 23, 15, 7]#Initial permut made on the key
CP_1 = [57, 49, 41, 33, 25, 17, 9,1, 58, 50, 42, 34, 26, 18,10, 2, 59, 51, 43, 35, 27,19, 11, 3, 60, 52, 44, 36,63, 55, 47, 39, 31, 23, 15,7, 62, 54, 46, 38, 30, 22,14, 6, 61, 53, 45, 37, 29,21, 13, 5, 28, 20, 12, 4]#Permut applied on shifted key to get Ki+1
CP_2 = [14, 17, 11, 24, 1, 5, 3, 28,15, 6, 21, 10, 23, 19, 12, 4,26, 8, 16, 7, 27, 20, 13, 2,41, 52, 31, 37, 47, 55, 30, 40,51, 45, 33, 48, 44, 49, 39, 56,34, 53, 46, 42, 50, 36, 29, 32]#Expand matrix to get a 48bits matrix of datas to apply the xor with Ki
E = [32, 1, 2, 3, 4, 5,4, 5, 6, 7, 8, 9,8, 9, 10, 11, 12, 13,12, 13, 14, 15, 16, 17,16, 17, 18, 19, 20, 21,20, 21, 22, 23, 24, 25,24, 25, 26, 27, 28, 29,28, 29, 30, 31, 32, 1]#SBOX
S_BOX = [[[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],[0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],[4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],
],[[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],[3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],[0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],[13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],
],[[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],[13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],[13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],[1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],
],[[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],[13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],[10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],[3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],
],  [[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],[14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],[4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],[11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],
], [[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],[10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],[9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],[4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],
], [[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],[13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],[1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],[6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],
],[[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],[1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],[7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],[2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11],
]
]#Permut made after each SBox substitution for each round
P = [16, 7, 20, 21, 29, 12, 28, 17,1, 15, 23, 26, 5, 18, 31, 10,2, 8, 24, 14, 32, 27, 3, 9,19, 13, 30, 6, 22, 11, 4, 25]#Final permut for datas after the 16 rounds
PI_1 = [40, 8, 48, 16, 56, 24, 64, 32,39, 7, 47, 15, 55, 23, 63, 31,38, 6, 46, 14, 54, 22, 62, 30,37, 5, 45, 13, 53, 21, 61, 29,36, 4, 44, 12, 52, 20, 60, 28,35, 3, 43, 11, 51, 19, 59, 27,34, 2, 42, 10, 50, 18, 58, 26,33, 1, 41, 9, 49, 17, 57, 25]#Matrix that determine the shift for each round of keys
SHIFT = [1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1]def string_to_bit_array(text):#Convert a string into a list of bitsarray = list()for char in text:binval = binvalue(char, 8)#Get the char value on one bytearray.extend([int(x) for x in list(binval)]) #Add the bits to the final listreturn arraydef bit_string_to_array(bitText):array = list()for bit in bitText.replace(" ",""):array.append(int(bit))return arraydef bit_array_to_string(array): #Recreate the string from the bit arrayres = ''.join([chr(int(y,2)) for y in [''.join([str(x) for x in _bytes]) for _bytes in  nsplit(array,8)]])return res# 根据ascil编码把字符转成对应的二进制
def binvalue(val, bitsize): #Return the binary value as a string of the given sizebinval = bin(val)[2:] if isinstance(val, int) else bin(ord(val))[2:]if len(binval) > bitsize:raise ("binary value larger than the expected size")while len(binval) < bitsize:binval = "0"+binval #Add as many 0 as needed to get the wanted sizereturn binvaldef nsplit(s, n):#Split a list into sublists of size "n"return [s[k:k+n] for k in range(0, len(s), n)]def showBits(s, n):#Split a list into sublists of size "n"return " ".join(["".join([str(i) for i in s[k:k+n]]) for k in range(0, len(s), n)])ENCRYPT=1
DECRYPT=0class des():def __init__(self):self.password = Noneself.text = Noneself.keys = list()def run(self, key, text, action=ENCRYPT):self.password = keyself.text = text# 产生所有子密钥self.generatekeys() #Generate all the keysresult = list()block = self.textblock = self.permut(block,PI)#Apply the initial permutationg, d = nsplit(block, 32) #g(LEFT), d(RIGHT)tmp = Nonefor i in range(16): #Do the 16 roundsd_e = self.expand(d, E) #Expand d to match Ki size (48bits)if action == ENCRYPT:tmp = self.xor(self.keys[i], d_e)#If encrypt use Kielse:tmp = self.xor(self.keys[15-i], d_e)#If decrypt start by the last keytmp = self.substitute(tmp) #Method that will apply the SBOXestmp = self.permut(tmp, P)tmp = self.xor(g, tmp)   # tmp = f(Rn-1,Kn)g = d   # Ln = Rn-1d = tmp # Rn = Ln-1 + f(Rn-1,Kn)print(f"L{i+1}:{showBits(g, 8)}")print(f"R{i + 1}:{showBits(d, 8)}")result += self.permut(d+g, PI_1) #Do the last permut and append the result to resultfinal_res = "".join([str(i) for i in result])return final_res# if padding and action==DECRYPT:#     return self.removePadding(final_res) #Remove the padding if decrypt and padding is true# else:#     return final_res #Return the final string of data ciphered/deciphereddef substitute(self, d_e):#Substitute bytes using SBOXsubblocks = nsplit(d_e, 6)#Split bit array into sublist of 6 bitsresult = list()for i in range(len(subblocks)): #For all the sublistsblock = subblocks[i]row = int(str(block[0])+str(block[5]),2)#Get the row with the first and last bitcolumn = int(''.join([str(x) for x in block[1:][:-1]]),2) #Column is the 2,3,4,5th bitsval = S_BOX[i][row][column] #Take the value in the SBOX appropriated for the round (i)bin = binvalue(val, 4)#Convert the value to binaryresult += [int(x) for x in bin]#And append it to the resulting listreturn result# 置换def permut(self, block, table):#Permut the given block using the given table (so generic method)return [block[x-1] for x in table]# 扩展def expand(self, block, table):#Do the exact same thing than permut but for more clarity has been renamedreturn [block[x-1] for x in table]def xor(self, t1, t2):#Apply a xor and return the resulting listreturn [x^y for x,y in zip(t1,t2)]def generatekeys(self):#Algorithm that generates all the keysself.keys = []# 把密钥转成这个形式 00110100 11000010.....key = self.passwordkey = self.permut(key, CP_1) #Apply the initial permut on the keyg, d = nsplit(key, 28) #Split it in to (g->LEFT),(d->RIGHT)for i in range(16):#Apply the 16 roundsg, d = self.shift(g, d, SHIFT[i]) #Apply the shift associated with the round (not always 1)tmp = g + d #Merge themself.keys.append(self.permut(tmp, CP_2)) #Apply the permut to get the Kidef shift(self, g, d, n): #Shift a list of the given valuereturn g[n:] + g[:n], d[n:] + d[:n]def addPadding(self):#Add padding to the datas using PKCS5 spec.pad_len = 8 - (len(self.text) % 8)self.text += pad_len * chr(pad_len)def removePadding(self, data):#Remove the padding of the plain text (it assume there is padding)pad_len = ord(data[-1])return data[:-pad_len]def encrypt(self, key, text):return self.run(key, text, ENCRYPT)def decrypt(self, key, text):return self.run(key, text, DECRYPT)if __name__ == '__main__':plain_text = bit_string_to_array("00000001 00100011 01000101 01100111 10001001 10101011 11001101 11101111")key = bit_string_to_array("00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001")d = des()r = d.encrypt(key,plain_text)print(r)# 测试cyberchefr = bit_string_to_array("01011010 11110101 00010101 10110000 01001011 11101111 01010010 01000001")r2 = d.decrypt(key,r)print("Ciphered: %r" % r)print("Deciphered: ", r2)# 07040502033636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636
#
# 6d6e6f68695c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c

l = [1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0]
def showBits(s, n):#Split a list into sublists of size "n"return " ".join(["".join([str(i) for i in s[k:k+n]]) for k in range(0, len(s), n)])print(showBits(l, 8))

CBC模式调用：

from pyDes import des, CBC, PAD_PKCS5
import binascii# 秘钥
KEY = 'Codeoooo'def des_encrypt(s):"""DES 加密:param s: 原始字符串:return: 加密后字符串，16进制"""secret_key = KEY  # 密码iv = secret_key  # 偏移# secret_key:加密密钥，CBC:加密模式，iv:偏移, padmode:填充des_obj = des(secret_key, CBC, iv, pad=None, padmode=PAD_PKCS5)# 返回为字节secret_bytes = des_obj.encrypt(s, padmode=PAD_PKCS5)# 返回为16进制return bytes.decode(binascii.b2a_hex(secret_bytes))def des_descrypt(s):"""DES 解密:param s: 加密后的字符串，16进制:return:  解密后的字符串"""secret_key = KEYiv = secret_keydes_obj = des(secret_key, CBC, iv, pad=None, padmode=PAD_PKCS5)decrypt_str = des_obj.decrypt(binascii.a2b_hex(s), padmode=PAD_PKCS5)return bytes.decode(decrypt_str)print(des_encrypt('codeooo'))
print(des_descrypt('4ff67fd9b661f01d'))

ECB模式调用：

from pyDes import des, ECB, PAD_PKCS5
import base64DES_SECRET_KEY = '12345678'
data = 'codeooo'
des_obj = des(DES_SECRET_KEY, ECB, DES_SECRET_KEY, padmode=PAD_PKCS5)
secret_bytes = str(base64.b64encode(des_obj.encrypt(data)), encoding = 'utf-8')
print(secret_bytes)


http://chatgpt.dhexx.cn/article/oByAj9Hn.shtml

相关文章

3DES加密算法原理及实现

3DES加密算法原理及实现

目录 引语 加密 加密算法公式 为什么采用加密-解密-加密的形式 解密 代码实现 注意&#xff1a;3DES是3重DES加解密算法&#xff0c;具体原理同DES,不在赘述。 引语 DES算法是全网公开的&#xff0c;其安全性是依靠秘钥的&#xff0c;但是随着计算机算力的增长&#xff…
阅读更多...
3DES加密算法原理

3DES加密算法原理

一、3DES加密算法简析&#xff1a; 3DES&#xff0c;也称为 3DESede 或 TripleDES&#xff0c;是三重数据加密算法&#xff0c;相当于是对每个数据库应用三次DES的对称加密算法。 由于DES密码长度容易被暴力破解&#xff0c;所以3DES算法通过对DES算法进行改进&#xff0c;增…
阅读更多...
简述3DES加密算法

简述3DES加密算法

之前我们聊了DES加密算法&#xff0c;在文章的最后我们提到了人们为了克服DES加密算法的不足&#xff0c;提出了三重DES&#xff0c;也就是3DES&#xff0c;今天我们就来简单了解一下它。 什么是3DES&#xff1f; 3DES&#xff0c;也称为3DESede或TripleDES&#xff0c;是三重数…
阅读更多...
图解DES、3DES和AES加密算法

图解DES、3DES和AES加密算法

文章目录 一、DES1. 加密和解密2. DES的结构(Feistel网络) 二、3DES1. 3DES加密2. 3DES解密 三、AES1. AES最终候选算法和算法确定2. Rijndael2.1 什么是Rijndael2.2 Rijndael的加密和解密 3. AES密钥生成4. AES算法流程图 一、DES 1. 加密和解密 DES是一种将64bit的明文加密…
阅读更多...
ArcGIS版本高级应用 数据归档（历史归档 存档数据）

ArcGIS版本高级应用 数据归档（历史归档 存档数据）

QQ交流群&#xff1a;607330463 GIS开发技术最强交流群 未经允许 禁止转载 可以参考 目录 1地理数据库 (Geodatabase) 存档 2启用存档 3存档过程 4使用历史版本 5使用历史标记 6使用地理数据库历史查看器 7直接使用存档类 8架构更改和存档 9禁用存档 10存档情景…
阅读更多...
文件归档功能

文件归档功能

在帮助大家运维EDI平台的这几年中&#xff0c;常常有些客户反馈为什么之前发送的数据页面上都没有了呢&#xff1f;我想查询下之前的数据是否有成功发送给我们的客户应该怎么确认呢&#xff1f;业务数据量太大&#xff0c;文件占用磁盘空间太多&#xff0c;我如何快速地确认一些…
阅读更多...
如何创建归档？

如何创建归档？

首先这里我们先了解两个概念归档和压缩&#xff0c;归档就相当于将文件批量打包在一块&#xff0c;便于之后工作查找文件的位置&#xff0c;但是总体文件的大小是不变的&#xff0c;例如我们将10个不通路径下且每个大小都是10M的文件打包在一块&#xff0c;那么归档后的大小就是…
阅读更多...
大数据归档-冷热数据分离

大数据归档-冷热数据分离

1. 什么是TokuDB&#xff1f; TokuDB 是一个支持事务的“新”引擎&#xff0c;有着出色的数据压缩功能&#xff0c;由美国 TokuTek 公司&#xff08;现在已经被 Percona 公司收购&#xff09;研发。拥有出色的数据压缩功能&#xff0c;如果您的数据写多读少&#xff0c;而且数…
阅读更多...
数据归档，存储的完美储备军

数据归档，存储的完美储备军

数据爆炸性增长的同时&#xff0c;存储成为了大家首要担心的问题 大家都希望自家数据保存20年、50年后仍完好无损 但是&#xff0c;N年后的数据量已达到一个无法预测的峰值 如此大量的数据在保存时极可能存在丢失、损坏等问题 这时需要提前对数据进行“备份”、“归档” 备份是…
阅读更多...
oracle数据库归档模式修改ARCHIVELOG

oracle数据库归档模式修改ARCHIVELOG

oracle数据库归档模式修改ARCHIVELOG 一、查看当前数据库的归档模式 第一步&#xff1a;查看oracle数据库的归档模式 命令如下&#xff1a;&#xff08;该命令登录sys用户可查&#xff09; select log_mode from v d a t a b a s e ; 如 果 值 为 N O A R C H I V E L O G &am…
阅读更多...
数据归档神器-pt-archiver

数据归档神器-pt-archiver

前言介绍 pt-archiver是用来归档表的工具&#xff0c;可以做到低影响、高性能的归档工具&#xff0c;从表中删除旧数据&#xff0c;而不会对 OLTP 查询产生太大影响。可以将数据插入到另一个表中&#xff0c;该表不需要在同一台服务器上。可以将其写入适合 LOAD DATA INFILE 的…
阅读更多...
从MYSQL 数据库归档 到 归档设计

从MYSQL 数据库归档 到 归档设计

到数据归档&#xff0c;很多人的第一个概念就是&#xff0c;不就是无用的数据&#xff0c;换个地方放吗&#xff0c;直接拷贝&#xff0c;删除不就得了&#xff0c;有那么麻烦。 我见到过的&#xff0c;听到过的数据库归档的方法有以下几种 1 数据通过人工的手段来进行清理&am…
阅读更多...
数据存储领域的“归档Archive”

数据存储领域的“归档Archive”

档案圈的朋友想必对档案领域的“归档”一词已经耳熟能详&#xff0c;按照DA/T 58-2014《电子档案管理基本术语》中的定义&#xff0c;归档&#xff08;Archiving&#xff09;是指“按照国家规定将具有保存价值的电子文件及其元数据的保管权交给档案部门的过程”。 今天我们要聊…
阅读更多...
那些年跟领导聊过的数据归档【DB篇】：从梳理到落地-DB单表千万级归档详细流程讲解

那些年跟领导聊过的数据归档【DB篇】：从梳理到落地-DB单表千万级归档详细流程讲解

文章目录 知人论世执笔蓝图V1 - 浅尝辄止V2 - 初窥门镜V3 - 木已成舟 躬行方案安内攘外 卓有成效沉淀之石道阻且长 知人论世 无论何种需求的出现都是因为某种迫切解决的问题契机&#xff0c;它是业务发展中定数也是劫数&#xff0c;近期DBA反馈磁盘存储空间超过80%不足以支撑未…
阅读更多...
进来偷学一招，数据归档二三事儿

进来偷学一招，数据归档二三事儿

Hello&#xff0c;大家好&#xff0c;我是楼下小黑哥~ 随着业务的快速增长&#xff0c;业务体量变得越来越大&#xff0c;这个过程我们会碰到各种问题&#xff0c;倒逼着我们进行技术升级。 那今天我们来聊下&#xff0c;这个过程将会碰到关于数据的问题。 数据增长带来的烦…
阅读更多...
MySQL 归档数据的方法你知道了吗

MySQL 归档数据的方法你知道了吗

归档&#xff0c;在 MySQL 中&#xff0c;是一个相对高频的操作。 它通常涉及以下两个动作&#xff1a; 迁移。将数据从业务实例迁移到归档实例。删除。从业务实例中删除已迁移的数据。 在处理类似需求时&#xff0c;都是开发童鞋提单给 DBA&#xff0c;由 DBA 来处理。 于…
阅读更多...
7.数据归档(Archiver)

7.数据归档(Archiver)

1.归档的基本概念 归档: 是指将数据写入文件存储到程序的沙盒中,当再次重新打开程序时,可以还原这些数据. 称它为数据序列化, 数据持久化. 临时数据: 存储在内存中的数据, 程序关闭, 内存释放,数据丢失数据持久性的方式 1) NSKeyedArchiver—-对象归档 2) NSUserDefaults 3)…
阅读更多...
如何用matlab求出矩阵简化阶梯形顺带算出主元所在的列

如何用matlab求出矩阵简化阶梯形顺带算出主元所在的列

matlab用rref函数 函数格式 [R,j]rref(A) A是矩阵 R是简化后的阶梯形 j是主元例子&#xff1a;求矩阵A的简化阶梯形与主元所在的列 >> A [1 1 -2 1 4; 2 4 -6 4 8; 2 -3 1 -1 2; 3 6 -9 7 9]; >> [R,j]rref(A)R 1 0 -1 0 40 1 -1 0 …
阅读更多...
（线性代数笔记）2.阶梯型矩阵

（线性代数笔记）2.阶梯型矩阵

1.阶梯形矩阵的定义 矩阵的主元 2.任意矩阵经过有限次初等行变换化为阶梯形 这里C是由B通过初等行变化得到的&#xff0c;C也是A的阶梯形 3.矩阵的秩 例题&#xff08;矩阵通过初等行变换转化为阶梯形&#xff09;
阅读更多...
行阶梯型矩阵，行最简形矩阵，标准形矩阵

行阶梯型矩阵，行最简形矩阵，标准形矩阵

行阶梯形矩阵&#xff1a; 行最简形矩阵&#xff1a; 标准形矩阵&#xff1a;
阅读更多...
推荐文章

Copyright @ 2022~2023