9、CNN 卷积神经网络

B站视频教程传送门：PyTorch深度学习实践 - 卷积神经网络（基础篇） PyTorch深度学习实践 - 卷积神经网络（高级篇）

9.1 Revision

全连接神经网络（Fully Connected Neural Network）：该网络完全由线形层Linear串行连接起来，即每一个输入节点都要参与到下一层任一输出节点的计算上。

class Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.l1 = torch.nn.Linear(784, 512)self.l2 = torch.nn.Linear(512, 256)self.l3 = torch.nn.Linear(256, 128)self.l4 = torch.nn.Linear(128, 64)self.l5 = torch.nn.Linear(64, 10)def forward(self, x):x = x.view(-1, 784)x = F.relu(self.l1(x))x = F.relu(self.l2(x))x = F.relu(self.l3(x))x = F.relu(self.l4(x))return self.l5(x)model = Net()

9.2 Introduction

Convolutional Neural Network

注意：

• $1\times 28\times 28<==>C\times W\times H$

• Convolution 卷积：保留图像的空间结构信息

• Subsampling 下采样（主要是 Max Pooling）：通道数不变，宽高改变，为了减少图像数据量，进一步降低运算的需求

• Fully Connected 全连接：将张量展开为一维向量，再进行分类

• 我们将 Convolution 及 Subsampling 等称为特征提取（Feature Extraction），最后的 Fully Connected 称为分类（Classification）。

9.3 Convolution

可以先了解一下 栅格图像 和 矢量图像 的区别与联系：

9.3.1 Channel

• Single Input Channel：

• 3 Input Channels：

其中，C H W 变化如下：

• N Input Channels：

• N Input Channels and M Output Channels

要想输出 M 通道的图像，卷积核也需设置为 M 个：

9.3.2 Layer

当输入为 $n\times widt{h}_{in}\times heigh{t}_{in}$ ，如何得到 $m\times widt{h}_{out}\times heigh{t}_{out}$ 的输出：

输出的通道数为 m，所以需要 m 个卷积核，且每个卷积核的尺寸为：$n\times kerne{l}_{width}\times kerne{l}_{height}$ ，即四维张量：
$$m\times n\times kerne{l}_{width}\times kerne{l}_{height}$$

import torchin_channels, out_channels = 5, 10
width, height = 100, 100
kernel_size = 3
batch_size = 1input = torch.randn(batch_size, in_channels, width, height)
conv_layer = torch.nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size)
output = conv_layer(input)print(input.shape)
print(conv_layer.weight.shape)  # m n w h
print(output.shape)

torch.Size([1, 5, 100, 100])
torch.Size([10, 5, 3, 3])
torch.Size([1, 10, 98, 98])

9.3.3 Padding

如果 $input=5\times 5$ ， $kernel=3\times 3$ ，并且希望 $output=5\times 5$，可以采取什么方法？

可以使用参数 padding=1 ，先将input填充至 $7\times 7$ ，这样卷积之后，output仍为 $5\times 5$ 。

import torchinput = [3, 4, 6, 5, 7,2, 4, 6, 8, 2,1, 6, 7, 8, 4,9, 7, 4, 6, 2,3, 7, 5, 4, 1]input = torch.Tensor(input).view(1, 1, 5, 5)  # B C W Hconv_layer = torch.nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=1, bias=False)  # O I W H
kernel = torch.Tensor([1, 2, 3, 4, 5, 6, 7, 8, 9]).view(1, 1, 3, 3)
conv_layer.weight.data = kernel.dataoutput = conv_layer(input)print(output)

tensor([[[[ 91., 168., 224., 215., 127.],[114., 211., 295., 262., 149.],[192., 259., 282., 214., 122.],[194., 251., 253., 169.,  86.],[ 96., 112., 110.,  68.,  31.]]]], grad_fn=<ConvolutionBackward0>)

9.3.4 Stride

参数 stride 意为步长，假设 $stride=2$ 时，kernel在向右或向下移动时，一次性移动两格，可以有效的降低图像的宽度和高度。

import torchinput = [3, 4, 6, 5, 7,2, 4, 6, 8, 2,1, 6, 7, 8, 4,9, 7, 4, 6, 2,3, 7, 5, 4, 1]input = torch.Tensor(input).view(1, 1, 5, 5)  # B C W Hconv_layer = torch.nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, stride=2, bias=False)  # O I W H
kernel = torch.Tensor([1, 2, 3, 4, 5, 6, 7, 8, 9]).view(1, 1, 3, 3)
conv_layer.weight.data = kernel.dataoutput = conv_layer(input)print(output)

tensor([[[[211., 262.],[251., 169.]]]], grad_fn=<ConvolutionBackward0>)

9.4 Max Pooling

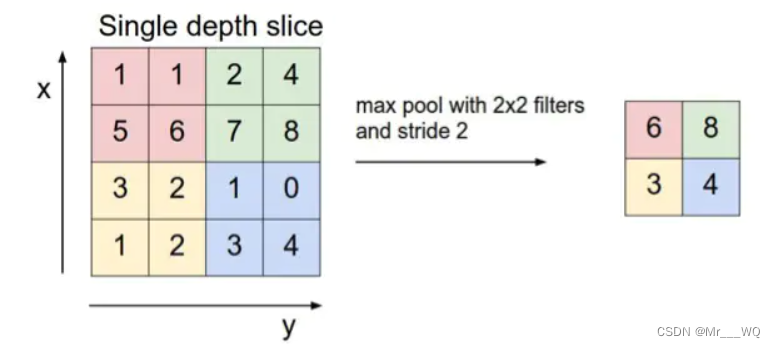
Max Pooling：最大池化，默认 $stride=2$ ，若 $kernel=2\times 2$ ，即在该表格中找出最大值：

import torchinput = [3, 4, 6, 5,2, 4, 6, 8,1, 6, 7, 8,9, 7, 4, 6]input = torch.Tensor(input).view(1, 1, 4, 4)
maxpooling_layer = torch.nn.MaxPool2d(kernel_size=2)
output = maxpooling_layer(input)print(output)

tensor([[[[4., 8.],[9., 8.]]]])

9.5 A Simple CNN

下图为一个简单的神经网络：

即：

代码如下：

class Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)self.pooling = torch.nn.MaxPool2d(2)self.fc = torch.nn.Linear(320, 10)def forward(self, x):# Flatten data from (n, 1, 28, 28) to (n, 784)batch_size = x.size(0)x = F.relu(self.pooling(self.conv1(x)))x = F.relu(self.pooling(self.conv2(x)))x = x.view(batch_size, -1)  # flattenx = self.fc(x)return xmodel = Net()

9.5.1 GPU

使用GPU来跑数据的前提：安装CUDA版PyTorch

• Move Model to GPU ：在调用模型后添加以下代码

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)

• Move Tensors to GPU ：训练和测试函数添加以下代码

inputs, target = inputs.to(device), target.to(device)

9.5.2 Code 1

import torch
from torchvision import transforms
from torch.utils.data import DataLoader
from torchvision import datasets
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as pltbatch_size = 64transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.1307,), (0.3081,))
])train_dataset = datasets.MNIST(root='../data/mnist', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)test_dataset = datasets.MNIST(root='../data/mnist', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)class Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)self.pooling = torch.nn.MaxPool2d(2)self.fc = torch.nn.Linear(320, 10)def forward(self, x):# Flatten data from (n, 1, 28, 28) to (n, 784)batch_size = x.size(0)x = F.relu(self.pooling(self.conv1(x)))x = F.relu(self.pooling(self.conv2(x)))x = x.view(batch_size, -1)  # flattenx = self.fc(x)return xmodel = Net()device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")  # GPU
model.to(device)criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)def train(epoch):running_loss = 0.0for batch_idx, data in enumerate(train_loader, 0):inputs, target = datainputs, target = inputs.to(device), target.to(device)  # GPUoptimizer.zero_grad()# forward + backward + updateoutputs = model(inputs)loss = criterion(outputs, target)loss.backward()optimizer.step()running_loss += loss.item()if batch_idx % 300 == 299:print('[%d, %3d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 2000))running_loss = 0.0accuracy = []def test():correct = 0total = 0with torch.no_grad():for data in test_loader:inputs, target = datainputs, target = inputs.to(device), target.to(device)  # GPUoutputs = model(inputs)_, predicted = torch.max(outputs.data, dim=1)total += target.size(0)correct += (predicted == target).sum().item()print('Accuracy on test set: %d %% [%d/%d]' % (100 * correct / total, correct, total))accuracy.append(100 * correct / total)if __name__ == '__main__':for epoch in range(10):train(epoch)test()print(accuracy)plt.plot(range(10), accuracy)plt.xlabel("Epoch")plt.ylabel("Accuracy")plt.grid()plt.show()

[1, 300] loss: 0.091
[1, 600] loss: 0.027
[1, 900] loss: 0.020
Accuracy on test set: 97 % [9700/10000]
[2, 300] loss: 0.017
[2, 600] loss: 0.014
[2, 900] loss: 0.013
Accuracy on test set: 97 % [9799/10000]
[3, 300] loss: 0.012
[3, 600] loss: 0.011
[3, 900] loss: 0.011
Accuracy on test set: 98 % [9813/10000]
[4, 300] loss: 0.010
[4, 600] loss: 0.009
[4, 900] loss: 0.009
Accuracy on test set: 98 % [9838/10000]
[5, 300] loss: 0.008
[5, 600] loss: 0.008
[5, 900] loss: 0.008
Accuracy on test set: 98 % [9846/10000]
[6, 300] loss: 0.007
[6, 600] loss: 0.008
[6, 900] loss: 0.007
Accuracy on test set: 98 % [9858/10000]
[7, 300] loss: 0.006
[7, 600] loss: 0.007
[7, 900] loss: 0.007
Accuracy on test set: 98 % [9869/10000]
[8, 300] loss: 0.006
[8, 600] loss: 0.006
[8, 900] loss: 0.006
Accuracy on test set: 98 % [9869/10000]
[9, 300] loss: 0.006
[9, 600] loss: 0.006
[9, 900] loss: 0.006
Accuracy on test set: 98 % [9849/10000]
[10, 300] loss: 0.005
[10, 600] loss: 0.005
[10, 900] loss: 0.005
Accuracy on test set: 98 % [9849/10000]
[97.0, 97.99, 98.13, 98.38, 98.46, 98.58, 98.69, 98.69, 98.49, 98.49]

9.5.3 Exercise

若对该神经网络进行改进：

• Conv2d Layer * 3
• ReLU Layer * 3
• MaxPooling Layer * 3
• Linear Layer * 3

$$\begin{gathered} input:1\times 28\times 28 \\ convolution:28-5+1=24,to:16\times 24\times 24 \\ pooling:16\times 12\times 12 \\ convolution:12-5+1=8,to:32\times 8\times 8 \\ pooling:20\times 4\times 4 \\ convolution:4-3+1=2,to:64\times 2\times 2 \\ pooling:64\times 1\times 1 \\ fc:64--32--16--10 \end{gathered}$$

9.5.4 Code 2

将神经网络改成如下即可：

    def __init__(self):super(Net, self).__init__()self.conv1 = torch.nn.Conv2d(1, 16, kernel_size=5)self.conv2 = torch.nn.Conv2d(16, 32, kernel_size=5)self.conv3 = torch.nn.Conv2d(32, 64, kernel_size=3)self.pooling = torch.nn.MaxPool2d(2)self.fc1 = torch.nn.Linear(64, 32)self.fc2 = torch.nn.Linear(32, 16)self.fc3 = torch.nn.Linear(16, 10)def forward(self, x):batch_size = x.size(0)x = self.pooling(F.relu(self.conv1(x)))x = self.pooling(F.relu(self.conv2(x)))x = self.pooling(F.relu(self.conv3(x)))x = x.view(batch_size, -1)x = F.relu(self.fc1(x))x = F.relu(self.fc2(x))x = self.fc3(x)return x

[1, 300] loss: 0.345
[1, 600] loss: 0.273
[1, 900] loss: 0.069
Accuracy on test set: 91 % [9194/10000]
[2, 300] loss: 0.034
[2, 600] loss: 0.025
[2, 900] loss: 0.020
Accuracy on test set: 96 % [9670/10000]
[3, 300] loss: 0.015
[3, 600] loss: 0.015
[3, 900] loss: 0.014
Accuracy on test set: 97 % [9754/10000]
[4, 300] loss: 0.011
[4, 600] loss: 0.010
[4, 900] loss: 0.011
Accuracy on test set: 98 % [9810/10000]
[5, 300] loss: 0.008
[5, 600] loss: 0.009
[5, 900] loss: 0.009
Accuracy on test set: 98 % [9808/10000]
[6, 300] loss: 0.008
[6, 600] loss: 0.007
[6, 900] loss: 0.008
Accuracy on test set: 98 % [9859/10000]
[7, 300] loss: 0.006
[7, 600] loss: 0.006
[7, 900] loss: 0.007
Accuracy on test set: 98 % [9862/10000]
[8, 300] loss: 0.005
[8, 600] loss: 0.006
[8, 900] loss: 0.006
Accuracy on test set: 97 % [9784/10000]
[9, 300] loss: 0.005
[9, 600] loss: 0.005
[9, 900] loss: 0.006
Accuracy on test set: 98 % [9842/10000]
[10, 300] loss: 0.005
[10, 600] loss: 0.005
[10, 900] loss: 0.004
Accuracy on test set: 98 % [9878/10000]
[91.94, 96.7, 97.54, 98.1, 98.08, 98.59, 98.62, 97.84, 98.42, 98.78]

9.6 GoogLeNet

注意：Convolution 、 Pooling 、 Softmax、 Other

若以上图来编写神经网络，则会有许多重复，为减少代码冗余，可以尽量多使用函数/类。

9.6.1 Inception Module

构造神经网络时，有一些超参数是难以选择的，比如卷积核Kernel，应该选择哪一种卷积核比较好用？

GoogLeNet在一个块中将几种卷积核（$1\times 1、3\times 3、5\times 5、...$）都使用，然后将其结果罗列到一起，将来通过训练自动找到一种最优的组合。

• Concatenate：将张量拼接到一块

• Average Pooling 均值池化：保证输入输出宽高一致（可借助padding和stride）

9.6.2 1 x 1 convolution

为什么要引入 $1 \times 1 $ convolution ？

见上图：若 $input=192\times 28\times 28,output=32\times 28\times 28$ ，则计算量 $Operations=5^2\times 28^2\times 192\times 32=120,422,400$

见上图：若在其中间使用 $convolution:1\times 1$ ，则计算量 $Operations=1^2\times 28^2\times 192\times 16+5^2\times 28^2\times 16\times 32=12,433,648$

9.6.3 Implementation of Inception Module

计算方向：由下至上

# 第一列
self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
branch_pool = self.branch_pool(branch_pool)# 第二列
self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)branch1x1 = self.branch1x1(x)# 第三列
self.branch5x5_1 = nn.Conv2d(in_channels,16, kernel_size=1)
self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)branch5x5 = self.branch5x5_1(x)
branch5x5 = self.branch5x5_2(branch5x5)# 第四列
self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)branch3x3 = self.branch3x3_1(x)
branch3x3 = self.branch3x3_2(branch3x3)
branch3x3 = self.branch3x3_3(branch3x3)

再进行拼接：

outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
return torch.cat(outputs, dim=1)

Using Inception Module：

class InceptionA(nn.Module):def __init__(self, in_channels):super(InceptionA, self).__init__()self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)def forward(self, x):branch1x1 = self.branch1x1(x)branch5x5 = self.branch5x5_1(x)branch5x5 = self.branch5x5_2(branch5x5)branch3x3 = self.branch3x3_1(x)branch3x3 = self.branch3x3_2(branch3x3)branch3x3 = self.branch3x3_3(branch3x3)branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)branch_pool = self.branch_pool(branch_pool)outputs = [branch1x1, branch5x5, branch3x3, branch_pool]return torch.cat(outputs, dim=1)

class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 10, kernel_size=5)self.conv2 = nn.Conv2d(88, 20, kernel_size=5)self.incep1 = InceptionA(in_channels=10)self.incep2 = InceptionA(in_channels=20)self.mp = nn.MaxPool2d(2)self.fc = nn.Linear(1408, 10)def forward(self, x):in_size = x.size(0)x = F.relu(self.mp(self.conv1(x)))x = self.incep1(x)x = F.relu(self.mp(self.conv2(x)))x = self.incep2(x)x = x.view(in_size, -1)x = self.fc(x)return x

完整代码：

import torch
from torch import nn
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt# 1、准备数据集
batch_size = 64transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.1307,), (0.3081,))
])train_dataset = datasets.MNIST(root='../data/mnist', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)test_dataset = datasets.MNIST(root='../data/mnist', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)# 2、建立模型
# 定义一个Inception类
class InceptionA(nn.Module):def __init__(self, in_channels):super(InceptionA, self).__init__()self.branch1X1 = nn.Conv2d(in_channels, 16, kernel_size=1)# 设置padding保证 宽 高 不变self.branch5X5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch5X5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)self.branch3X3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)self.branch3X3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)self.branch3X3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)def forward(self, x):branch1X1 = self.branch1X1(x)branch5X5 = self.branch5X5_1(x)branch5X5 = self.branch5X5_2(branch5X5)branch3X3 = self.branch3X3_1(x)branch3X3 = self.branch3X3_2(branch3X3)branch3X3 = self.branch3X3_3(branch3X3)branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)branch_pool = self.branch_pool(branch_pool)outputs = [branch1X1, branch5X5, branch3X3, branch_pool]# （b, c, w, h），dim=1 以第一个维度channel来拼接return torch.cat(outputs, dim=1)# 定义模型
class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 10, kernel_size=5)# 88 = 24*3 + 16self.conv2 = nn.Conv2d(88, 20, kernel_size=5)self.incep1 = InceptionA(in_channels=10)self.incep2 = InceptionA(in_channels=20)self.mp = nn.MaxPool2d(2)# 确定输出张量的尺寸# 在定义时先不定义fc层，随便选取一个输入，经过模型后查看其尺寸# 在init函数中把fc层去掉，forward函数中把最后两行去掉，确定输出的尺寸后再定义Lear层的大小self.fc = nn.Linear(1408, 10)def forward(self, x):in_size = x.size(0)# 1 --> 10x = F.relu(self.mp(self.conv1(x)))# 10 --> 88x = self.incep1(x)# 88 --> 20x = F.relu(self.mp(self.conv2(x)))# 20 --> 88x = self.incep2(x)x = x.view(in_size, -1)x = self.fc(x)return xmodel = Net()
# 将模型迁移到GPU上运行
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)# 3、建立损失函数和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)# 4、定义训练函数
def train(epoch):running_loss = 0for batch_idx, data in enumerate(train_loader, 0):inputs, target = data# 将计算的张量迁移到GPU上inputs, target = inputs.to(device), target.to(device)optimizer.zero_grad()# 前馈 反馈 更新outputs = model(inputs)loss = criterion(outputs, target)loss.backward()optimizer.step()running_loss += loss.item()if batch_idx % 300 == 299:print('[%d, %3d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))running_loss = 0# 5、定义测试函数
accuracy = []def test():correct = 0total = 0with torch.no_grad():for data in test_loader:images, labels = data# 将测试中的张量迁移到GPU上images, labels = images.to(device), labels.to(device)outputs = model(images)_, predicted = torch.max(outputs.data, dim=1)total += labels.size(0)# 得出其中相等元素的个数correct += (predicted == labels).sum().item()print('Accuracy on test set: %d %% [%d/%d]' % (100 * correct / total, correct, total))accuracy.append(100 * correct / total)if __name__ == '__main__':for epoch in range(10):train(epoch)test()print(accuracy)plt.plot(range(10), accuracy)plt.xlabel("Epoch")plt.ylabel("Accuracy")plt.grid()  # 表格plt.show()

[1, 300] loss: 0.836
[1, 600] loss: 0.196
[1, 900] loss: 0.145
Accuracy on test set: 96 % [9690/10000]
[2, 300] loss: 0.106
[2, 600] loss: 0.099
[2, 900] loss: 0.091
Accuracy on test set: 97 % [9785/10000]
[3, 300] loss: 0.075
[3, 600] loss: 0.078
[3, 900] loss: 0.071
Accuracy on test set: 98 % [9831/10000]
[4, 300] loss: 0.064
[4, 600] loss: 0.067
[4, 900] loss: 0.061
Accuracy on test set: 98 % [9845/10000]
[5, 300] loss: 0.057
[5, 600] loss: 0.058
[5, 900] loss: 0.052
Accuracy on test set: 98 % [9846/10000]
[6, 300] loss: 0.051
[6, 600] loss: 0.049
[6, 900] loss: 0.050
Accuracy on test set: 98 % [9852/10000]
[7, 300] loss: 0.047
[7, 600] loss: 0.043
[7, 900] loss: 0.045
Accuracy on test set: 98 % [9848/10000]
[8, 300] loss: 0.039
[8, 600] loss: 0.044
[8, 900] loss: 0.042
Accuracy on test set: 98 % [9871/10000]
[9, 300] loss: 0.041
[9, 600] loss: 0.034
[9, 900] loss: 0.041
Accuracy on test set: 98 % [9866/10000]
[10, 300] loss: 0.032
[10, 600] loss: 0.038
[10, 900] loss: 0.037
Accuracy on test set: 98 % [9881/10000]
[96.9, 97.85, 98.31, 98.45, 98.46, 98.52, 98.48, 98.71, 98.66, 98.81]

9.7 Residual Net

如果将 $3\times 3$ 的卷积一直堆下去，该神经网络的性能会不会更好？

Paper：He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[C]// IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2016:770-778.

研究发现：20 层的错误率低于56 层的错误率，所以并不是层数越多，性能越好。为解决 梯度消失 的问题，见下图：

多一个 跳连接 ：

9.7.1 Residual Network

class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 16, kernel_size=5)self.conv2 = nn.Conv2d(16, 32, kernel_size=5)self.mp = nn.MaxPool2d(2)self.rblock1 = ResidualBlock(16)self.rblock2 = ResidualBlock(32)self.fc = nn.Linear(512, 10)def forward(self, x):in_size = x.size(0)x = self.mp(F.relu(self.conv1(x)))x = self.rblock1(x)x = self.mp(F.relu(self.conv2(x)))x = self.rblock2(x)x = x.view(in_size, -1)x = self.fc(x)return x

9.7.2 Residual Block

class ResidualBlock(nn.Module):def __init__(self, channels):super(ResidualBlock, self).__init__()self.channels = channelsself.conv1 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)self.conv2 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)def forward(self, x):y = F.relu(self.conv1(x))y = self.conv2(y)return F.relu(x + y)

9.7.3 Code 3

import torch
from torch import nn
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as pltbatch_size = 64transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.1307,), (0.3081,))
])train_dataset = datasets.MNIST(root='../data/mnist', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)test_dataset = datasets.MNIST(root='../data/mnist', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)class ResidualBlock(nn.Module):def __init__(self, channels):super(ResidualBlock, self).__init__()self.channels = channelsself.conv1 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)self.conv2 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)def forward(self, x):y = F.relu(self.conv1(x))y = self.conv2(y)return F.relu(x + y)class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = nn.Conv2d(1, 16, kernel_size=5)self.conv2 = nn.Conv2d(16, 32, kernel_size=5)self.mp = nn.MaxPool2d(2)self.rblock1 = ResidualBlock(16)self.rblock2 = ResidualBlock(32)self.fc = nn.Linear(512, 10)def forward(self, x):in_size = x.size(0)x = self.mp(F.relu(self.conv1(x)))x = self.rblock1(x)x = self.mp(F.relu(self.conv2(x)))x = self.rblock2(x)x = x.view(in_size, -1)x = self.fc(x)return xmodel = Net()device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)def train(epoch):running_loss = 0for batch_idx, data in enumerate(train_loader, 0):inputs, target = datainputs, target = inputs.to(device), target.to(device)optimizer.zero_grad()outputs = model(inputs)loss = criterion(outputs, target)loss.backward()optimizer.step()running_loss += loss.item()if batch_idx % 300 == 299:print('[%d, %3d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))running_loss = 0accuracy = []def test():correct = 0total = 0with torch.no_grad():for data in test_loader:images, labels = dataimages, labels = images.to(device), labels.to(device)outputs = model(images)_, predicted = torch.max(outputs.data, dim=1)total += labels.size(0)correct += (predicted == labels).sum().item()print('Accuracy on test set: %d %% [%d/%d]' % (100 * correct / total, correct, total))accuracy.append(100 * correct / total)if __name__ == '__main__':for epoch in range(10):train(epoch)test()print(accuracy)plt.plot(range(10), accuracy)plt.xlabel("Epoch")plt.ylabel("Accuracy")plt.grid()plt.show()

[1, 300] loss: 0.563
[1, 600] loss: 0.157
[1, 900] loss: 0.111
Accuracy on test set: 97 % [9721/10000]
[2, 300] loss: 0.085
[2, 600] loss: 0.077
[2, 900] loss: 0.081
Accuracy on test set: 98 % [9831/10000]
[3, 300] loss: 0.063
[3, 600] loss: 0.059
[3, 900] loss: 0.053
Accuracy on test set: 98 % [9841/10000]
[4, 300] loss: 0.047
[4, 600] loss: 0.052
[4, 900] loss: 0.042
Accuracy on test set: 98 % [9877/10000]
[5, 300] loss: 0.039
[5, 600] loss: 0.037
[5, 900] loss: 0.041
Accuracy on test set: 98 % [9871/10000]
[6, 300] loss: 0.035
[6, 600] loss: 0.032
[6, 900] loss: 0.035
Accuracy on test set: 98 % [9895/10000]
[7, 300] loss: 0.029
[7, 600] loss: 0.032
[7, 900] loss: 0.029
Accuracy on test set: 98 % [9899/10000]
[8, 300] loss: 0.026
[8, 600] loss: 0.028
[8, 900] loss: 0.025
Accuracy on test set: 98 % [9892/10000]
[9, 300] loss: 0.021
[9, 600] loss: 0.027
[9, 900] loss: 0.024
Accuracy on test set: 98 % [9886/10000]
[10, 300] loss: 0.019
[10, 600] loss: 0.021
[10, 900] loss: 0.023
Accuracy on test set: 99 % [9902/10000]
[97.21, 98.31, 98.41, 98.77, 98.71, 98.95, 98.99, 98.92, 98.86, 99.02]

9.7.4 Reading Paper

Paper 1：He K, Zhang X, Ren S, et al. Identity Mappings in Deep Residual Networks[C]

constant scaling：

class ResidualBlock(nn.Module):def __init__(self, channels):super(ResidualBlock, self).__init__()self.channels = channelsself.conv1 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)self.conv2 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)def forward(self, x):y = F.relu(self.conv1(x))y = self.conv2(x)z = 0.5 * (x + y)return F.relu(z)

[1, 300] loss: 1.204
[1, 600] loss: 0.243
[1, 900] loss: 0.165
Accuracy on test set: 96 % [9637/10000]
[2, 300] loss: 0.121
[2, 600] loss: 0.105
[2, 900] loss: 0.099
Accuracy on test set: 97 % [9777/10000]
[3, 300] loss: 0.085
[3, 600] loss: 0.076
[3, 900] loss: 0.069
Accuracy on test set: 98 % [9815/10000]
[4, 300] loss: 0.061
[4, 600] loss: 0.063
[4, 900] loss: 0.063
Accuracy on test set: 98 % [9849/10000]
[5, 300] loss: 0.053
[5, 600] loss: 0.052
[5, 900] loss: 0.052
Accuracy on test set: 98 % [9853/10000]
[6, 300] loss: 0.041
[6, 600] loss: 0.051
[6, 900] loss: 0.047
Accuracy on test set: 98 % [9871/10000]
[7, 300] loss: 0.040
[7, 600] loss: 0.044
[7, 900] loss: 0.043
Accuracy on test set: 98 % [9869/10000]
[8, 300] loss: 0.039
[8, 600] loss: 0.038
[8, 900] loss: 0.037
Accuracy on test set: 98 % [9859/10000]
[9, 300] loss: 0.031
[9, 600] loss: 0.039
[9, 900] loss: 0.036
Accuracy on test set: 98 % [9875/10000]
[10, 300] loss: 0.035
[10, 600] loss: 0.031
[10, 900] loss: 0.033
Accuracy on test set: 98 % [9888/10000]
[96.37, 97.77, 98.15, 98.49, 98.53, 98.71, 98.69, 98.59, 98.75, 98.88]

conv shortcut：

class ResidualBlock(nn.Module):    def __init__(self, channels):super(ResidualBlock, self).__init__()self.channels = channelsself.conv1 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)self.conv2 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)self.conv3 = nn.Conv2d(channels, channels, kernel_size=1)def forward(self, x):y = F.relu(self.conv1(x))y = self.conv2(x)z = self.conv3(x) + yreturn F.relu(z)

[1, 300] loss: 0.760
[1, 600] loss: 0.170
[1, 900] loss: 0.119
Accuracy on test set: 97 % [9717/10000]
[2, 300] loss: 0.092
[2, 600] loss: 0.084
[2, 900] loss: 0.075
Accuracy on test set: 98 % [9826/10000]
[3, 300] loss: 0.064
[3, 600] loss: 0.063
[3, 900] loss: 0.055
Accuracy on test set: 98 % [9817/10000]
[4, 300] loss: 0.048
[4, 600] loss: 0.047
[4, 900] loss: 0.048
Accuracy on test set: 98 % [9851/10000]
[5, 300] loss: 0.039
[5, 600] loss: 0.039
[5, 900] loss: 0.044
Accuracy on test set: 98 % [9864/10000]
[6, 300] loss: 0.035
[6, 600] loss: 0.033
[6, 900] loss: 0.038
Accuracy on test set: 98 % [9890/10000]
[7, 300] loss: 0.030
[7, 600] loss: 0.030
[7, 900] loss: 0.030
Accuracy on test set: 98 % [9881/10000]
[8, 300] loss: 0.027
[8, 600] loss: 0.026
[8, 900] loss: 0.029
Accuracy on test set: 98 % [9884/10000]
[9, 300] loss: 0.021
[9, 600] loss: 0.026
[9, 900] loss: 0.025
Accuracy on test set: 98 % [9894/10000]
[10, 300] loss: 0.019
[10, 600] loss: 0.019
[10, 900] loss: 0.025
Accuracy on test set: 98 % [9897/10000]
[97.17, 98.26, 98.17, 98.51, 98.64, 98.9, 98.81, 98.84, 98.94, 98.97]

Paper 2：Huang G, Liu Z, Laurens V D M, et al. Densely Connected Convolutional Networks[J]. 2016:2261-2269.