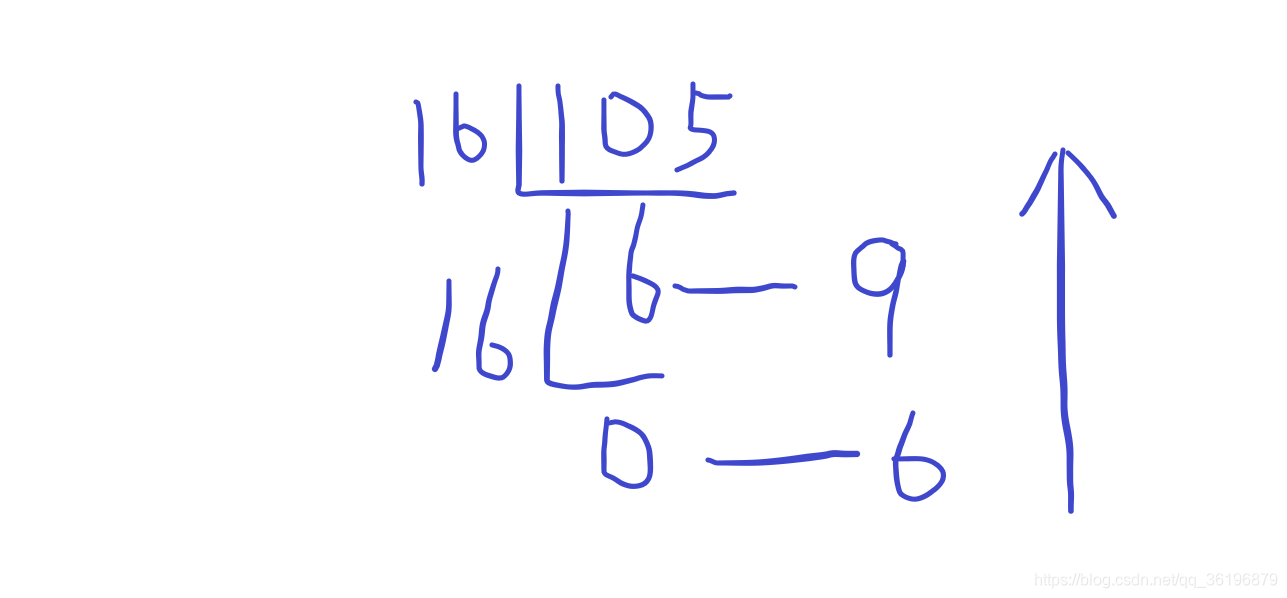一.基本概念

数制：计数的方法，指用一组固定的符号和统一的规则表示数值的方法
数位：指数字符号在一个数中所处的位置
基数：指在某种进位计数制中，数位上所能使用的数字符号的个数
位权：指在某种进位数制中，数位所代表的大小，即处在某一位上的“1”所代表的数值的大小

二.计算机的数值

我们一般说的百兆、千兆网络单位是bps（比特率，即位/秒，bit
/s）比如我们说网卡或光纤的传输速度是百兆，也就是100Mbps的意思。而在实际应用中（迅雷等下载工具）使用的传输单位是字节/秒（Byte/s）
Byte是字节，而bit是二进制单元
8bit=1byte
1024byte=1kb
1024kb=1Mb

1.KIB、MIB与KB、MB的区别

好多人以为KB与KIB是同一种单位的不同缩写，其实这是两种不同的计算方式。具体的差别是MB是单位以10为底层的指数，Mib是以2为底层的指数。如1Kb=10^{3=1000；1Kib=2}10=1024。
与我们密切相关的是我们在买硬盘的时候，操作系统报的数量要比产品标出或商家号称的小一些，主要原因是标出的是以Mb、Gb为单位的，1Gb就是1000000000Byte，而操作系统是以2进制为处理单位的因此检查硬盘容量时是以Mib、Gib为单位，1Gb=2^30=1073741824，相比较而言，1Gib要比1Gb多出73741824，所以检测实际结果要比标出少一些。

2.数值的表示

B表示二进制数；O表示八进制；D表示十进制数；H表示十六进制数

二进制（Binary number） （1010）2；1010B
十进制（Decimal number） (1010)10；1010D；1010
八进制（octal Number） （1010）8，1010O
十六进制（Hexadecimal） （1010）16；1010H；0X1010

三.进制转换

计算机采用的是二进制，因此二进制具有运算简单，易实现且可靠。还有八进制、十六进制作为二进制的缩写。一般计数都采用进位计数，其特点是：（逢N进一）二进制：逢二进一，借一当二。八进制：逢八进一，借一当八。十六进制:逢十六进一，借一当十六。

十进制：有十个基数，0123456789。
二进制:有两个基数，01。
八进制：有八个基数，01234567。
十六进制：有十六个基数，0——9，A——F。（A=10,B=11,C=12,D=13,E=14,F=15）

1.十进制的转换

1.1十进制二进制的转换

十进制→二进制：十进制数除以2，初至0时所得余数按反方向写出，即为二进制数。
例：十进制数37

所以转换成的二进制数字为:100101
二进制→十进制：二进制数从低位到高位（即从右往左）计算，第0位的权值是2的0次方，第1位的权值是2的1次方，第2位的权值是2的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了。
例：将二进制的(101011)B转换为十进制的步骤如下：

1. 第0位 1 x 2^0 = 1；

2. 第1位 1 x 2^1 = 2；

3. 第2位 0 x 2^2 = 0；

4. 第3位 1 x 2^3 = 8；

5. 第4位 0 x 2^4 = 0；

6. 第5位 1 x 2^5 = 32；

7. 读数，把结果值相加，1+2+0+8+0+32=43

1.2十进制八进制的转换

十进制→八进制：十进制数主次整除8，直至商为0，所得余数按照相反顺序写出，即为其八进制数。
例:2456
2456/8=307，余0；
307/8=38，余3；
38/8=4，余6；
4/8=0，余4。
将所有余数倒序相连，得到结果：4630。
八进制→十进制：八进制数从低位到高位（即从右往左）计算，第0位的权值是8的0次方，第1位的权值是8的1次方，第2位的权值是8的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了。
例：将八进制的(53)O转换为十进制
1 第0位 3 x 8^0 = 3；
2 第1位 5 x 8^1 = 40；
3 读数，把结果值相加，3+40=43

1.3十进制十六进制的转换

十进制→十六进制：十进制数整除16，直至商为0，所得余数按相反顺序写出，即为十六进制数。
例：1610转换成十六进制
1610/16=100……10(A)；
100 /16= 6……4；
6 /16= 0……6；
余数倒数相连得：1610(10)=64A(16).
十六进制→十进制：十六进制数从低位到高位（即从右往左）计算，第0位的权值是16的0次方，第1位的权值是16的1次方，第2位的权值是16的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了。
例：将十六进制的(2B)H转换为十进制的步骤如下：
1第0位 B x 16^0 = 11；
2 第1位 2 x 16^1 = 32；
3读数，把结果值相加，11+32=43

2.二进制八进制十六进制的转换

2.1二进制八进制的转换

二进制→八进制：对于整数，采用从右到左每三位一组，不够三位的在其左边补齐0，每组单独转换出来，即为八进制数。
例：（001 101 111 011）
1 5 7 3

八进制→二进制：将每位八进制由三位二进制数代替，即可完成转换。
例：（ 1 7 3 5 ）
001 111 011 101

2.2二进制与十六进制的转换

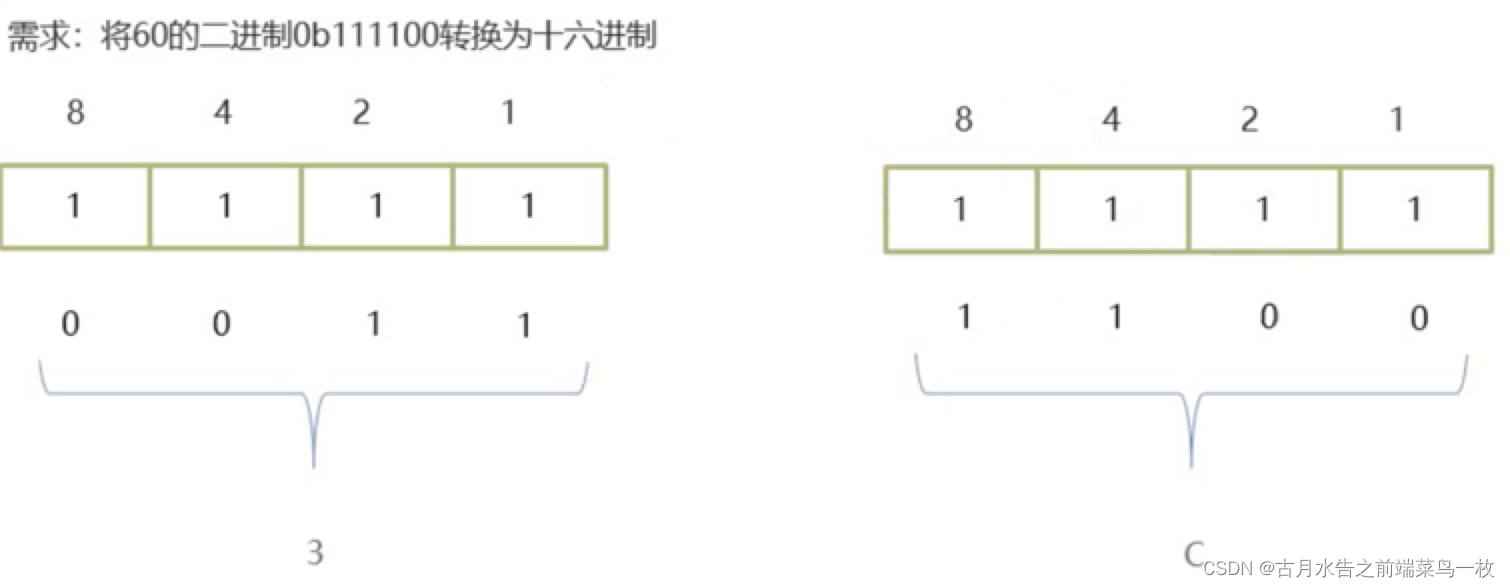
二进制→十六进制：将二进制数的没四位用一个十六进制数码来表示，整数部分以小数点为界点从右往左每四位一组转换，小数部分从小数点开始自左向右每四位一组进行转换。
例：（1001 0111 0111 1001）
9 7 7 9
十六进制→二进制：只要将每一位十六进制数用四位相应的二进制数表示，即可完成转换
例：（ 8 7 6 5 ）
1000 0111 0110 0101

2.3八进制十六进制的转换

我们可以先把八进制的数字转换成二进制，在从二进制转换成十六进制
例：八进制的：1234567
转换为二进制是每个数字转换为三位二进制：001 010 011 100 101 110 111
然后把这些数字从右边开始进行按四位分组：0 0101 0011 1001 0111 0111
然后从右边每四位组依次对应一个16进制数：053977

四.总结：

1.十进制与二进制、八进制、十六进制间可相互转化，二进制与八进制、十进制、十六进制间可相互转化，但八进制与十六进制间不可直接转化，必须以二进制或十进制作为工具，一般采用因简便多二进制。
2.二进制与八进制转化注意是3个位数，二进制与十六进制转化注意是4个位数。
3.各进制在日常生活中的作用
10进制，当然是便于我们人类来使用，我们从小的习惯就是使用十进制，这个毋庸置疑。
2进制，是供计算机使用的，1，0代表开和关，有和无，机器只认识2进制。
16进制，内存地址空间是用16进制的数据表示, 如0x8049324。