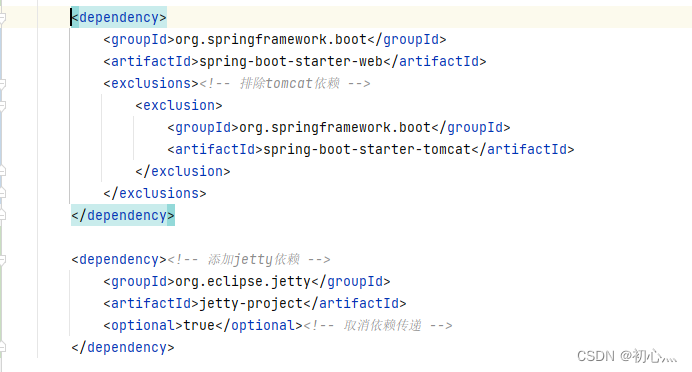
给定一个数组 ，让你找出一个最长上升子序列的长度，例如[1,4,6,2,3,5]
答案为4：[1,2,3,5]。

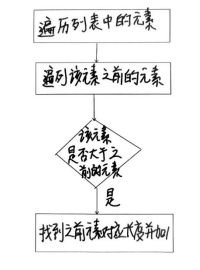
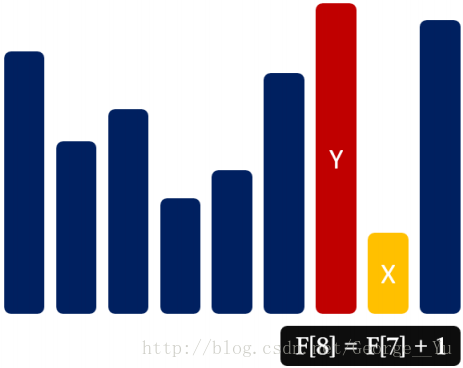
我们用DP[i]表示以下标为i的元素结尾的子序列的最长上升子序列长度

代码如下：

ll p[10010];
ll dp[10010];
int main()
{ll n, ans = 0;cin >> n;for (int i = 1; i <= n; i++)cin >> p[i];for (int i = 1; i <= n; i++){for (int j = 1; j < i; j++){if (p[i] > p[j])dp[i] = max(dp[i], dp[j] + 1);}ans = max(dp[i] + 1, ans);}cout << ans << endl;return 0;
}

下面是今天下午没写出来的一个题，LIS其实很早就看到过了，也是很简单的DP，一直没写，说来惭愧。

智算之道 网格

这个我写了好久，中间都快自己写出LIS了，可惜一直差一点。看完LIS就很简单了。

我们可以发现，如果可以当前在魔法方格上并且2*W1<W2，那么肯定选择一步走到右上角。而且如果只用方式一移动，那么代价是确定的，2*n*W1，因此其实就是找，最多可以经过几个魔法方格。

那么就是找最长上升子点（坐标？）了。

代码：

struct node
{ll x, y;bool operator<(const node &temp) const{if (x == temp.x)return y < temp.y;return x < temp.x;}
} p[2010];
ll dp[2010];
int main()
{ll n, k, w1, w2, ans = 0;cin >> n >> k >> w1 >> w2;for (int i = 1; i <= k; i++)cin >> p[i].x >> p[i].y;if (w1 * 2 <= w2)return cout << 2 * n * w1 << endl, 0;sort(p + 1, p + 1 + k);for (int i = 1; i <= k; i++){for (int j = 1; j < i; j++){if (p[i].x > p[j].x && p[i].y > p[j].y)dp[i] = max(dp[i], dp[j] + 1);}ans = max(ans, dp[i] + 1);}cout << 2 * n * w1 - ans * (2 * w1 - w2) << endl;return 0;
}