哈夫曼树-创建，编码，解码，带权路径长度（含全部代码）

article/2025/10/2 9:19:22

目录

主要函数

所选实例

创建哈夫曼树

步骤

【分析】

哈夫曼树结构

注意项

代码

创建哈夫曼树结果截图

编码

【分析】

代码

哈夫曼树编码结果截图

解码

【分析】

代码

哈夫曼树解码结果截图

计算带权路径长度

【分析】

代码

计算带权路径长度结果截图

全部代码

主要函数

void CreateHT()创建哈夫曼树
void Code() 哈夫曼树编码
void Encode() 哈夫曼树解码
void WPL() 计算带权路径长度

所选实例

所选实例

 

创建哈夫曼树

步骤

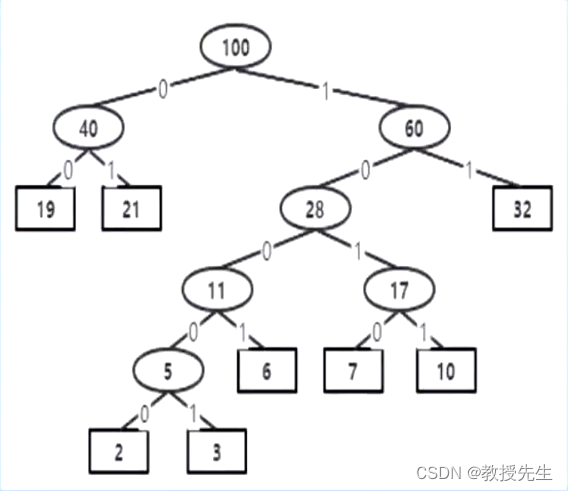
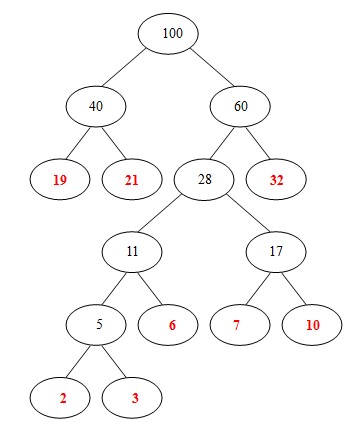
假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

【分析】

采用双亲孩子表示法，存在数组之中，记录下标。辅助函数进行两棵根权值最小的树的选择，用标志数组标志是否已加入哈夫曼树。

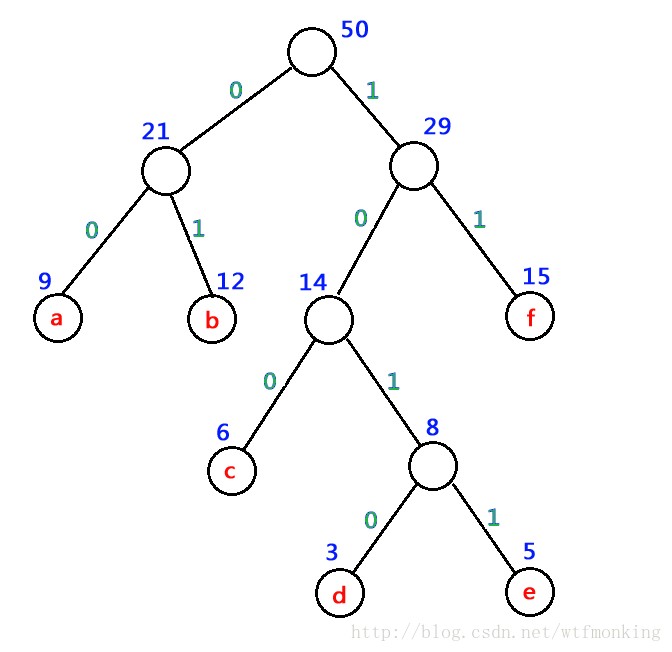
哈夫曼树结构

//哈夫曼树结点结构
typedef struct HNode 
{char data; //数据,非叶节点为NULLdouble weight;//权重int parent;//双亲，-1表示没有双亲，即根节点int lchild;//左孩子，数组下标,-1表示无左孩子，即叶节点int rchild;//右孩子
}Hnode;

注意项

辅助函数进行两棵最小权值树的挑选时，可能只剩下最后一棵树，注意进行判断。

代码

//创建哈夫曼树
void CreateHT()
{int n;//字符个数，即哈夫曼树叶节点个数minnodes mins;cout << "请输入字符个数：" << endl;cin >> n;cout << "请输入字符及权值：" << endl;for (int i=0;i<n;i++){cin >> HT[i].data >> HT[i].weight;HT[i].lchild = -1;HT[i].rchild = -1;}/*HT[0].data = 'a';HT[0].weight = 45;HT[0].lchild = -1;HT[0].rchild = -1;HT[1].data = 'b';HT[1].weight = 13;HT[1].lchild = -1;HT[1].rchild = -1;HT[2].data = 'c';HT[2].weight = 12;HT[2].lchild = -1;HT[2].rchild = -1;HT[3].data = 'd';HT[3].weight = 16;HT[3].lchild = -1;HT[3].rchild = -1;HT[4].data = 'e';HT[4].weight = 9; HT[4].lchild = -1;HT[4].rchild = -1;HT[5].data = 'f';HT[5].weight = 5; HT[5].lchild = -1;HT[5].rchild = -1;*/int i = n;for (;;i++){mins = Select(i);//找到两棵根权值最小的树if (mins.flag == false)//仅剩余一棵树时跳出{HT[mins.m1].parent = -1;break;}			HT[i].weight = HT[mins.m1].weight + HT[mins.m2].weight;//新加入哈夫曼树结点为两个结点权值之和HT[i].data = ' ';HT[mins.m1].parent = i;                                //两个权值最小结点双亲为新加入结点HT[mins.m2].parent = i;HT[i].lchild = mins.m1;//左小又大HT[i].rchild = mins.m2;} PrintHT(i);//打印哈夫曼树
}

创建哈夫曼树结果截图

创建结果截图

编码

【分析】

从叶子结点出发，向根前进，进一步进行判断，左孩子为0,右孩子为1。最后逆序保存即可。这里用了reverse函数，HC就是哈夫曼树叶节点的备份，加了编码，也可直接将编码作为哈夫曼树结点的属性，那样不太好，不需要编码时冗余，所以又弄了一个数组。

代码

//哈夫曼树编码
void Code()
{int i = 0;for (;;i++)//给所有叶子结点编码{int j = i;string str="";HC[i].data = HT[i].data;//复制数据while (-1!=HT[j].parent)//从叶节点找到根{if (HT[HT[j].parent].lchild == j)//左0右1{str += '0';}else{str += '1';}j = HT[j].parent;}reverse(str.begin(),str.end());//逆序HC[i].code = str;              //保存至编码if (HT[i].lchild == -1 && HT[i].rchild == -1)continue;//非叶子不编码else break;}PrintHC(i);
}

哈夫曼树编码结果截图

哈夫曼树编码截图

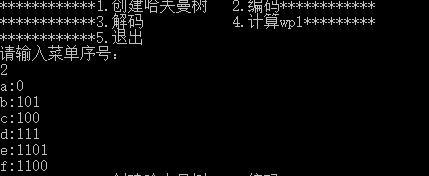
解码

【分析】

解码就是编码的逆过程，从根开始，左0右1,到叶节点输出。再回到根节点重复即可。

代码

//哈夫曼树解码 从根开始，左0右1，直至叶节点
void Encode() 
{string s;int root=0;//记录根节点的下标cout << "请输入01字符串:" << endl;cin >> s;while (HT[root].parent != -1) root++;int j = root;for (int i=0;i<s.length();i++)//遍历输入的01串{if ('0' == s[i]){j = HT[j].lchild;}else{j = HT[j].rchild;}if (HT[j].lchild == -1 && HT[j].rchild == -1)//到达叶节点{cout << HT[j].data;j = root;//返回根节点继续}}cout << endl;
}

哈夫曼树解码结果截图

哈夫曼树解码结果截图

计算带权路径长度

【分析】

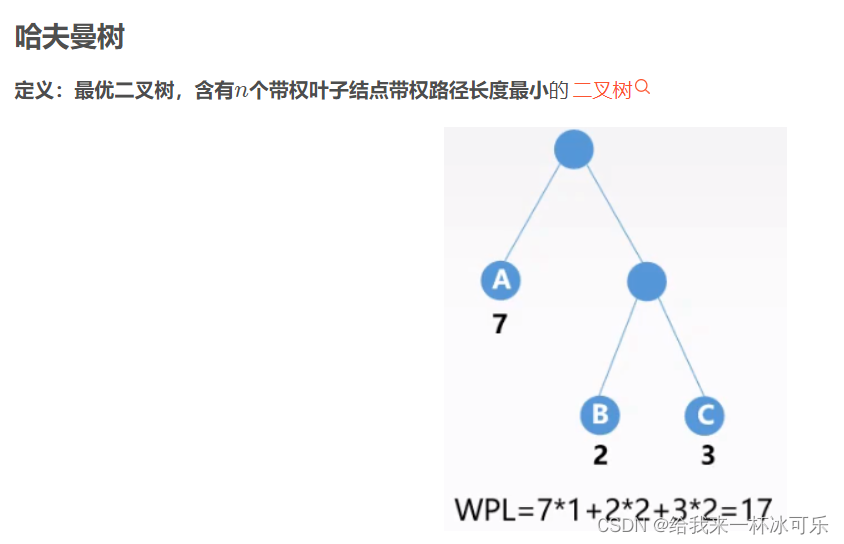
树的带权路径长度为所有叶节点的带权路径长度之和。叶节点的带权路径长度即叶节点的权值与从根节点到叶节点的路径长度之积。前面已经算过编码，用编码长度代替路径长度即可。本篇文章不针对某题，如果有题仅需计算带权路径长度，就仿照编码那段代码，从根出发计算路径长度，不用记录01即可。

代码

//计算WPL
void WPL() 
{double WPL=0;for (int i = 0;;i++){if (HT[i].lchild != -1 || HT[i].rchild != -1)break;WPL += HT[i].weight*HC[i].code.length();//权值×路径长度（编码长度）	}cout << "WPL:" << WPL << endl;
}

计算带权路径长度结果截图

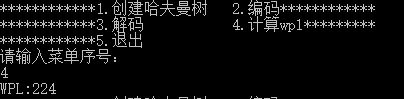
计算带权路径长度结果截图

全部代码

/*
Project:哈夫曼树 构造 编码 译码 计算wpl
Date:    2019/02/04
Author:  Frank Yu
void CreateHT()创建哈夫曼树
void Code() 哈夫曼树编码
void Encode() 哈夫曼树解码
void WPL() 计算带权路径长度
*/
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<string>
#include<set>
#include<list>
#include<vector>
#include<map>
#include<iterator>
#include<algorithm>
#include<iostream>
#define MAX 1000 //哈夫曼树最大结点个数
#define MAXW 1000 //权值最大
using namespace std;
//哈夫曼树结点结构
typedef struct HNode
{char data; //数据,非叶节点为NULLdouble weight;//权重int parent;//双亲，-1表示没有双亲，即根节点int lchild;//左孩子，数组下标,-1表示无左孩子，即叶节点int rchild;//右孩子
}Hnode;
//编码结构
typedef struct HCNode
{char data; //数据string code;//该字符编码
}Hcnode;
//两个最小结点下标
struct minnodes
{int m1;//两者更小权值结点下标int m2;bool flag;//若找到则为true,否则为false，false说明仅有一个结点
};
//辅助标志数组 标记该结点为根的树是否已加入哈夫曼树
bool flag[MAX] = { false };
Hnode HT[MAX];//哈夫曼树
Hcnode HC[MAX];//哈夫曼编码数组			   //选择两棵最小权值的树 参数max，当前有权值结点下标+1
minnodes Select(int max)
{double min = MAXW;minnodes mins;mins.m2 = -1;//查找第一个最小权值的结点下标for (int i = 0; i < max; i++){if (!flag[i] && HT[i].weight < min)//未加入哈夫曼树,权值更小{min = HT[i].weight;//更新最小权值mins.m1 = i;}}flag[mins.m1] = true;//将结点加入哈夫曼树min = MAXW;//查找第二个最小权值结点下标，可能不存在for (int i = 0; i < max; i++){if (!flag[i] && HT[i].weight < min)//未加入哈夫曼树,权值更小{min = HT[i].weight;//更新最小权值mins.m2 = i;}}flag[mins.m2] = true;//将结点加入哈夫曼树if (-1 == mins.m2)//仅剩余一个结点未加入哈夫曼树{mins.flag = false;//未找到两棵最小权值树}else{mins.flag = true;}return mins;
}
//打印哈夫曼树
void PrintHT(int max)
{cout << "下标\t" << "数据\t" << "权重\t" << "双亲\t" << "左孩子\t" << "右孩子" << endl;for (int i = 0; i<max; i++){cout << i << "\t" << HT[i].data << "\t" << HT[i].weight << "\t" << HT[i].parent << "\t" << HT[i].lchild << "\t" << HT[i].rchild << endl;}
}
//打印编码
void PrintHC(int n)
{for (int i = 0; i < n; i++){cout << HC[i].data << ":" << HC[i].code << endl;;}
}
//创建哈夫曼树
void CreateHT()
{int n;//字符个数，即哈夫曼树叶节点个数minnodes mins;cout << "请输入字符个数：" << endl;cin >> n;cout << "请输入字符及权值：" << endl;for (int i = 0; i<n; i++){cin >> HT[i].data >> HT[i].weight;HT[i].lchild = -1; HT[i].rchild = -1;}/*HT[0].data = 'a';HT[0].weight = 45;HT[0].lchild = -1;HT[0].rchild = -1;HT[1].data = 'b';HT[1].weight = 13;HT[1].lchild = -1;HT[1].rchild = -1;HT[2].data = 'c';HT[2].weight = 12;HT[2].lchild = -1;HT[2].rchild = -1;HT[3].data = 'd';HT[3].weight = 16;HT[3].lchild = -1;HT[3].rchild = -1;HT[4].data = 'e';HT[4].weight = 9; HT[4].lchild = -1;HT[4].rchild = -1;HT[5].data = 'f';HT[5].weight = 5; HT[5].lchild = -1;HT[5].rchild = -1;*/int i = n;for (;; i++){mins = Select(i);//找到两棵根权值最小的树if (mins.flag == false)//仅剩余一棵树时跳出{HT[mins.m1].parent = -1;break;}HT[i].weight = HT[mins.m1].weight + HT[mins.m2].weight;//新加入哈夫曼树结点为两个结点权值之和HT[i].data = ' ';HT[mins.m1].parent = i;                                //两个权值最小结点双亲为新加入结点HT[mins.m2].parent = i;HT[i].lchild = mins.m1;//左小又大HT[i].rchild = mins.m2;}PrintHT(i);//打印哈夫曼树
}
//哈夫曼树编码
void Code()
{int i = 0;for (;; i++)//给所有叶子结点编码{int j = i;string str = "";HC[i].data = HT[i].data;//复制数据while (-1 != HT[j].parent)//从叶节点找到根{if (HT[HT[j].parent].lchild == j)//左0右1{str += '0';}else{str += '1';}j = HT[j].parent;}reverse(str.begin(), str.end());//逆序HC[i].code = str;              //保存至编码if (HT[i].lchild == -1 && HT[i].rchild == -1)continue;//非叶子不编码else break;}PrintHC(i);
}
//哈夫曼树解码 从根开始，左0右1，直至叶节点
void Encode()
{string s;int root = 0;//记录根节点的下标cout << "请输入01字符串:" << endl;cin >> s;while (HT[root].parent != -1) root++;int j = root;for (int i = 0; i<s.length(); i++)//遍历输入的01串{if ('0' == s[i]){j = HT[j].lchild;}else{j = HT[j].rchild;}if (HT[j].lchild == -1 && HT[j].rchild == -1)//到达叶节点{cout << HT[j].data;j = root;//返回根节点继续}}cout << endl;
}
//计算WPL
void WPL()
{double WPL = 0;for (int i = 0;; i++){if (HT[i].lchild != -1 || HT[i].rchild != -1)break;WPL += HT[i].weight*HC[i].code.length();//权值×路径长度（编码长度）	}cout << "WPL:" << WPL << endl;
}
//菜单
void menu()
{cout << "************1.创建哈夫曼树   2.编码************" << endl;cout << "************3.解码           4.计算wpl*********" << endl;cout << "************5.退出" << endl;
}
//主函数
int main()
{int choice = 0;while (1){menu();printf("请输入菜单序号：\n");scanf("%d", &choice);if (5 == choice) break;switch (choice){case 1:CreateHT(); break;case 2:Code(); break;case 3:Encode(); break;case 4:WPL(); break;default:printf("输入错误！！！\n"); break;}}return 0;
}

更多数据结构与算法实现：数据结构（严蔚敏版）与算法的实现（含全部代码）

有问题请下方评论，转载请注明出处，并附有原文链接，谢谢！如有侵权，请及时联系。


http://chatgpt.dhexx.cn/article/m8Nvb2F1.shtml

相关文章

4,5,6,7,8作为叶子结点的权值构造哈夫曼树,则带权路径长度是

4,5,6,7,8作为叶子结点的权值构造哈夫曼树,则带权路径长度是

WPL&#xff08;45&#xff09;*3&#xff08;876&#xff09;*269
阅读更多...
求哈夫曼的带权路径长度

求哈夫曼的带权路径长度

【问题描述】 已知输入两行正整数&#xff0c;第二行正整数之间用空格键分开&#xff0c;请建立一个哈夫曼树&#xff0c;以输入的数字为叶节点&#xff0c;求这棵哈夫曼树的带权路径长度。 【输入形式】 首先第一行为输入正整数的个数&#xff0c;然后接下来的一行正整数&a…
阅读更多...
构造哈夫曼树以及求哈夫曼编码、树的带权路径长度

构造哈夫曼树以及求哈夫曼编码、树的带权路径长度

我们先搞清楚这几个概念 构造哈夫曼树的方法 将每种字符出现的频率先收集起来放在最上方&#xff0c;然后选择两个频率最小的增加到图中&#xff0c;并将他们的和作为他们的父节点&#xff0c;增加到图中&#xff0c;在最上方删除选择的两个节点&#xff08;4和2&#xff09;&a…
阅读更多...
哈夫曼树的构建与最小带权路径长度

哈夫曼树的构建与最小带权路径长度

注意&#xff1a;哈夫曼树并不唯一&#xff0c;但带权路径长度一定是相同的。 二叉树&#xff1a;每个结点最多含有两个子树的树称为二叉树。定理&#xff1a;对于具有n个叶子结点的哈夫曼树,共有2n-1个结点。 哈夫曼树介绍 1哈夫曼树的定义 哈夫曼&#xff08;Huffman&…
阅读更多...
创建哈夫曼树并求带权路径长度

创建哈夫曼树并求带权路径长度

创建哈夫曼树并求带权路径长度 【问题描述】根据给定的权重&#xff0c;构造哈夫曼树&#xff0c;输出其带权路径长度。 【输入形式】输入权重&#xff0c;空格作为分隔&#xff0c;回车结束&#xff0c;权重个数小于10。 【输出形式】哈夫曼树的带权路径长度。 【样例输入】5…
阅读更多...
哈夫曼树（构建以及计算加权路径长度）

哈夫曼树（构建以及计算加权路径长度）

今天做远景的笔试题&#xff0c;遇到了这么一道题&#xff0c;求{11,8,6,5,2}构成的哈夫曼树的加权路径长度。 好长时间没看数据结构&#xff0c;居然忘记怎么求了&#xff0c;该死。 考完下百度&#xff0c;好多答案居然都是错的。或者是光有答案没有过程。在这里把哈夫曼树的…
阅读更多...
哈夫曼树的构建、编码以及带权路径长计算

哈夫曼树的构建、编码以及带权路径长计算

给定n个权值作为n个叶子结点&#xff0c;构造一棵二叉树&#xff0c;若该树的带权路径长度达到最小&#xff0c;称这样的二叉树为最优二叉树&#xff0c;也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树&#xff0c;权值较大的结点离根较近。 构造哈夫曼树的算…
阅读更多...
哈夫曼树与带权路径长度

哈夫曼树与带权路径长度

问题&#xff1a; 权值分别为从19&#xff0c;21&#xff0c;2&#xff0c;3&#xff0c;6&#xff0c;7&#xff0c;10&#xff0c;32的结点&#xff0c;构造一棵哈夫曼树&#xff0c;该树的带权路径长度是&#xff1f; 哈夫曼树的一个应用&#xff1a; 压缩字符串https://…
阅读更多...
哈夫曼树 和 树的带权路径长度

哈夫曼树 和 树的带权路径长度

树的带权路径长度(Weighted Path Length of Tree)&#xff1a;定义为树中所有叶结点的带权路径长度之和。 结点的带权路径长度&#xff1a;结点到树根之间的路径长度与该结点上权的乘积。 哈夫曼树是一种带权路径长度最短的二叉树&#xff0c;也称为最优二叉树。 哈夫曼树构建…
阅读更多...
哈夫曼树的带权路径长度的算法

哈夫曼树的带权路径长度的算法

计算方法&#xff1a; ①先对集合中的结点按照权值从小到大排。 ②选两个权值最小的结点&#xff0c;将它们的权值相加构成一个新结点&#xff0c;原来的这两个最小的结点是新结点的左右子结点。 ③在有序集合中将两个被加过的结点去掉&#xff0c;再把新的结点放入集合中排…
阅读更多...
哈夫曼树结构和带权路径长度计算

哈夫曼树结构和带权路径长度计算

什么是哈夫曼树呢&#xff1f; 哈夫曼树是一种带权路径长度最短的二叉树&#xff0c;也称为最优二叉树。下面用一幅图来说明。 它们的带权路径长度分别为&#xff1a; 图a&#xff1a; WPL5*27*22*213*254 图b&#xff1a; WPL5*32*37*213*148 可见&#xff0c;图b的带权路径长…
阅读更多...
哈夫曼树结构及带权路径长度

哈夫曼树结构及带权路径长度

哈夫曼树&#xff1a; 当用 n 个结点&#xff08;都做叶子结点且都有各自的权值&#xff09;试图构建一棵树时&#xff0c;如果构建的这棵树的带权路径长度最小&#xff0c;称这棵树为“最优二叉树”&#xff0c;有时也叫“赫夫曼树”或者“哈夫曼树”。 在构建哈弗曼树时&…
阅读更多...
哈弗曼树的带权路径长度

哈弗曼树的带权路径长度

最近刷题刷到了这一题&#xff0c;此题是北邮往年复试题&#xff0c;看了一些网上的讲解&#xff0c;大多数是方法比较复杂&#xff0c;有些巧妙的方法又往往却缺少解释&#xff0c;为了方便大家理解&#xff0c;给小伙伴们梳理梳理 题目描述&#xff1a; 哈夫曼树&#xff0…
阅读更多...
哈夫曼树带权路径长度

哈夫曼树带权路径长度

一. 长什么样&#xff1f; 左边是普通树&#xff0c;右边是哈夫曼树 图a&#xff1a; WPL5*27*22*213*254 图b&#xff1a; WPL5*32*37*213*148 可见&#xff0c;图b的带权路径长度较小&#xff0c;我们可以证明图b就是哈夫曼树(也称为最优二叉树)。 二. 怎么生成和计算&…
阅读更多...
哈夫曼树、带权路径长度、前缀编码 的概念

哈夫曼树、带权路径长度、前缀编码 的概念

文章目录 一、基本概念1.1带权路径长度&#xff08;WPL&#xff09;1.2哈夫曼树 二、哈夫曼树的构造三、哈夫曼树的应用3.1哈夫曼编码与前缀编码 一、基本概念 1.1带权路径长度&#xff08;WPL&#xff09; 路径长度&#xff1a; 经历的边数 结点的带权路径长度&#xff1a; …
阅读更多...
树学习（2）

树学习（2）

1、 一颗哈夫曼树的带权路径长度等于其中所有分支结点的权值之和。&#xff08;错误&#xff09; 分析&#xff1a; 树的带权路径长度&#xff1a;定义为树中所有叶结点的带权路径长度之和&#xff1b;&#xff08;即等于所有结点&#xff08;叶结点分支结点&#xff0…
阅读更多...
哈夫曼树 带权路径

哈夫曼树 带权路径

树的带权路径长度 &#xff08;Weighted Path Length of Tree&#xff0c;简记为WPL&#xff09; 一般的&#xff0c;我们是可以用常规的构造哈夫曼树求带权路径长度。 计算结点的带权路径长度&#xff1a;结点到树根之间的路径长度与该结点上权的乘积。 带权路径长度WPL&a…
阅读更多...
求Huffman树的带权路径长度

求Huffman树的带权路径长度

Huffman树的建立过程&#xff1a; 首先得到整个叶子结点的集合&#xff1a; 求Huffman树的带权路径长度算法&#xff1a; 书上讲常见的求Huffman树的带权路径长度算法为&#xff1a;从叶子结点权值乘路径长度&#xff1a; WPL7*25*25*23*32*349 另外一种求WPL的算法为&…
阅读更多...
运行startx报错的解决

运行startx报错的解决

CentOS启动图形界面startx&#xff1a;xauth: file /root/.serverauth.1164 does not exist 运行如下命令 yum update yum groupinstall "X Window System" yum groupinstall "Desktop"报错无法解决问题. 继续运行如下命令 yum grouplist看到了一行: …
阅读更多...
linux startx xinit

linux startx xinit

startx启动过程分析 startx 及xinit 介绍(经典) startx启动过程 startx用法&#xff1a; startx [ [ client ] options ... ] [ -- [ server ] [ display ] options ... ]startx三种启动方式&#xff1a; 1 指定client和server&#xff0c; 例如&#xff1a;startx /usr/bin…
阅读更多...
推荐文章

Copyright @ 2022~2023