创建哈夫曼树并求带权路径长度

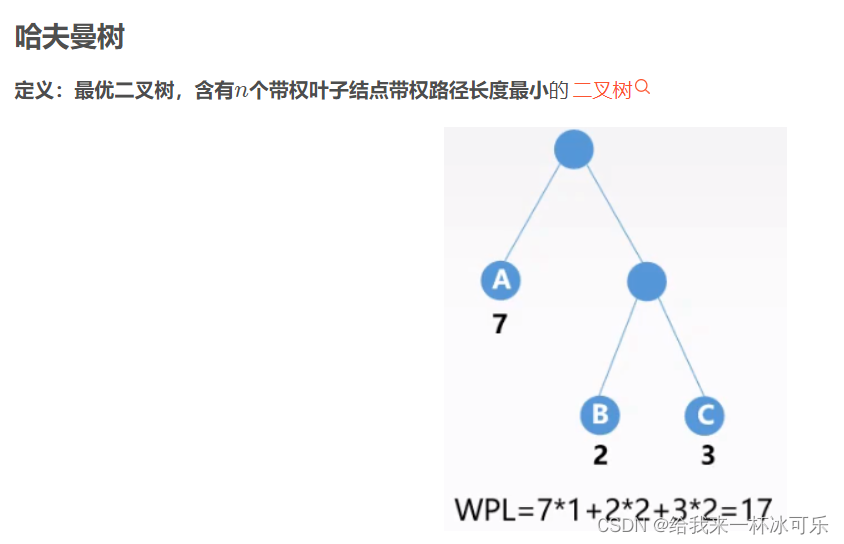
【问题描述】根据给定的权重，构造哈夫曼树，输出其带权路径长度。
【输入形式】输入权重，空格作为分隔，回车结束，权重个数小于10。
【输出形式】哈夫曼树的带权路径长度。
【样例输入】5 6 2 9 7
【样例输出】65
【样例说明】
【评分标准】

#include<iostream>
#include<cstdlib>
#include<cstdio>
#define MAX_SIZE 10
#define MAX 100
using namespace std;
typedef struct
{int weight;int parent, lchild, rchild;
}HTNode, *HuffmanTree;
void Select(HuffmanTree HT, int k, int &s1, int &s2)       //在HT[1...i-1]中选择parent为0，且weight最小的两个结点，分别赋给s1,s2
{int i, min;min = MAX;for (i = 1; i <= k; i++){if (HT[i].parent == 0 && min > HT[i].weight){s1 = i;min = HT[i].weight;}}min = MAX;for (i = 1; i <= k; i++){if (i != s1 && HT[i].parent == 0 && HT[i].weight < min){s2 = i;min = HT[i].weight;}}
}
void CreateHuffmanTree(HuffmanTree &HT, int *w, int n)     //创建哈夫曼树，不求哈夫曼编码HC
{int m, i, s1, s2;if (n <= 1)return;m = 2 * n - 1;HT = new HTNode[m + 1];for (i = 1; i <= m; i++){HT[i].weight = i <= n ? w[i - 1] : 0;HT[i].parent = HT[i].lchild = HT[i].rchild = 0;}s1 = s2 = 0;for (i = n + 1; i <= m; i++)                           //建哈夫曼树{Select(HT, i - 1, s1, s2);HT[i].lchild = s1;HT[i].rchild = s2;HT[s1].parent = HT[s2].parent = i;HT[i].weight = HT[s1].weight + HT[s2].weight;}
}
void PrintHuffmanTree(HuffmanTree HT, int n)
{int m, i;m = 2 * n - 1;for (i = 1; i <= m; i++){cout << i << "   " << HT[i].weight << "   " << HT[i].parent << "   " << HT[i].lchild << "   " << HT[i].rchild << endl;}
}
int WeightedPathLength(HuffmanTree HT, int n)              //求带权路径的长度
{int len, i, k, t;len = t = 0;for (i = 1; i <= n; i++){                                                      //哈夫曼树的特性决定：每一个双亲必有左右孩子，根节点除外for (k = HT[i].parent, t = 0; k != 0; k = HT[k].parent)                          //到根节点结束，即求出了路径长度t++;len += HT[i].weight*t;}return len;
}
int main(void)
{int n, len, w[MAX_SIZE];HuffmanTree HT;n = 0;do                                                     //输入权重,按回车结束{cin >> w[n];n++;} while (getchar() != '\n');CreateHuffmanTree(HT, w, n);len = WeightedPathLength(HT, n);cout << len << endl;system("pause");return 0;
}

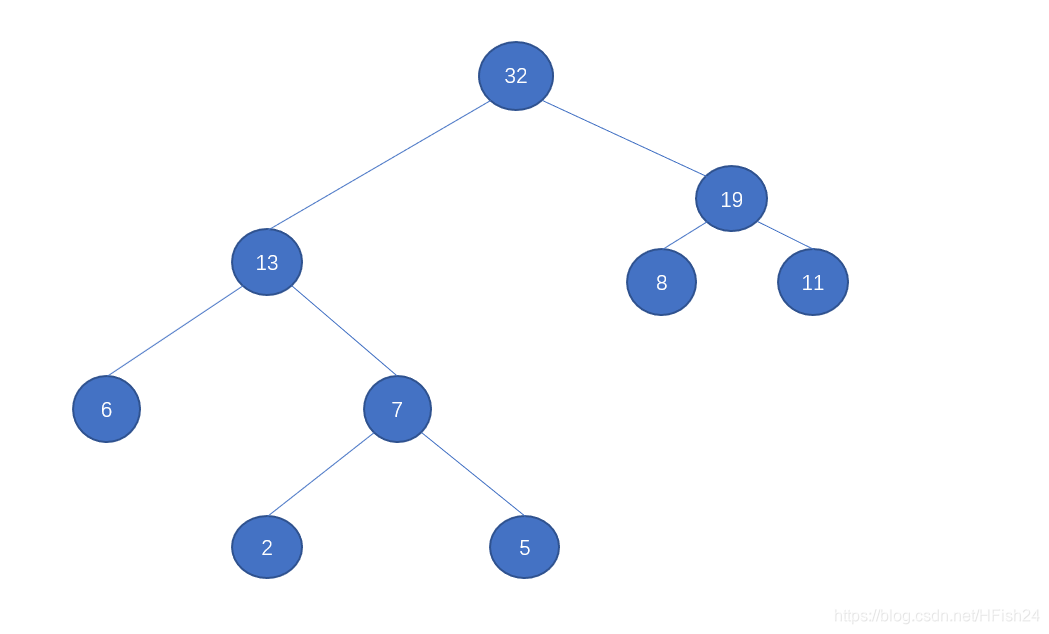
用例二叉树：

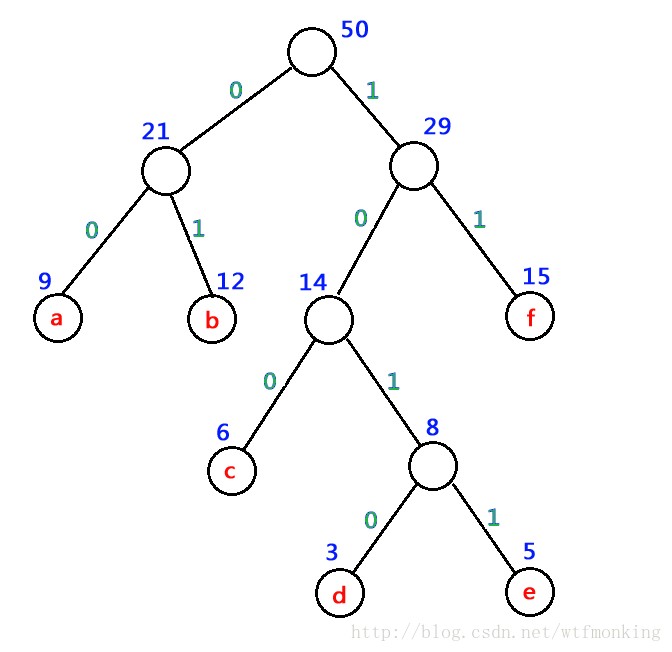
存储结构：

运行案例：

说明：
1.在哈夫曼树的构造过程中，需要频繁地访问结点的双亲，故采用静态三叉链表。
2.n个叶子结点的哈夫曼树，结点总数是确定的，共有2n-1个结点。
3.哈夫曼树上只含有度为0和度为2的结点，不存在度为1的结点。
4.构造n个权值的哈夫曼树，共需进新n-1次合并。