树的带权路径长度

（Weighted Path Length of Tree，简记为WPL）

一般的，我们是可以用常规的构造哈夫曼树求带权路径长度。

计算结点的带权路径长度：结点到树根之间的路径长度与该结点上权的乘积。

带权路径长度WPL（Weighted Path Length）最小的二叉树，也称为最优二又树。

在这里简单举个例子说一下：

题目：

给定6个字符（a,b,c,d,e,f）,它们的权值集合W =(2,3,4,7,8,9),试构造关于W的一棵哈夫曼树，求其带权路径长度WPL。

解：根据题意构造关于W的哈夫曼树如1图所示：

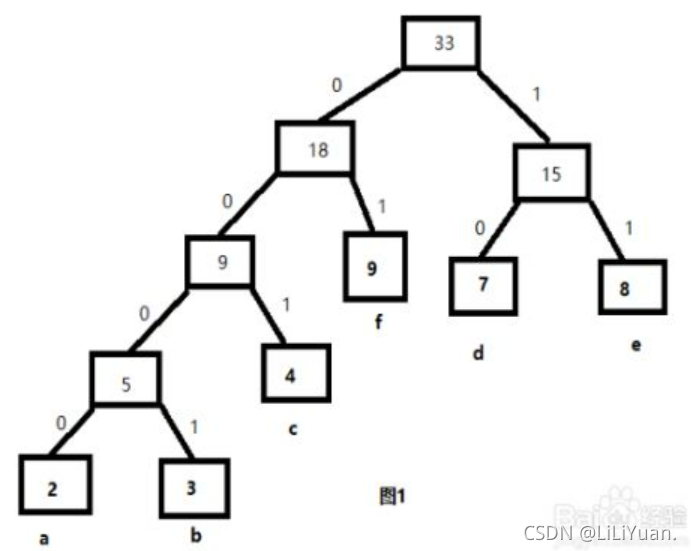
那么其带权路径长度WPL=(9+7+8)×2+4×3+(2+3)×4=80。

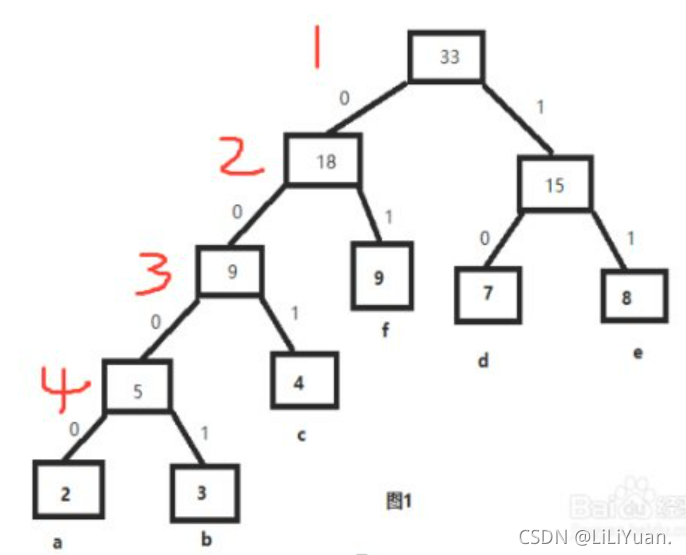
（结点到树根之间的路径长度与该结点上权的乘积）

哈夫曼树

构造哈夫曼树的办法是：在W中选出两个权小结点，并同时计算出它们的和，如果两个数的和正好是下一步的两个最小数的其中的一个，那么这个树直接往上生长就可以了，如果这两个数的和比较大，不是下一步的两个最小数的其中一个，那么就并列生长。

哈夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1L1+W2L2+W3L3+…+WnLn），N个权值Wi（i=1,2,…n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,…n），可以证明哈夫曼树的WPL是最小的。