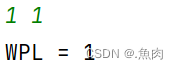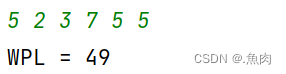Huffman树的建立过程：

首先得到整个叶子结点的集合：

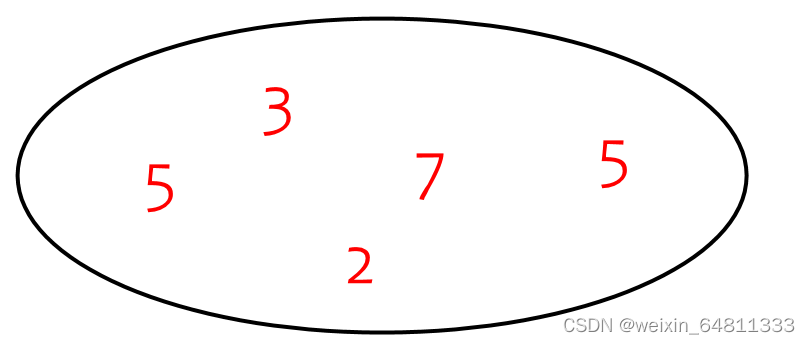
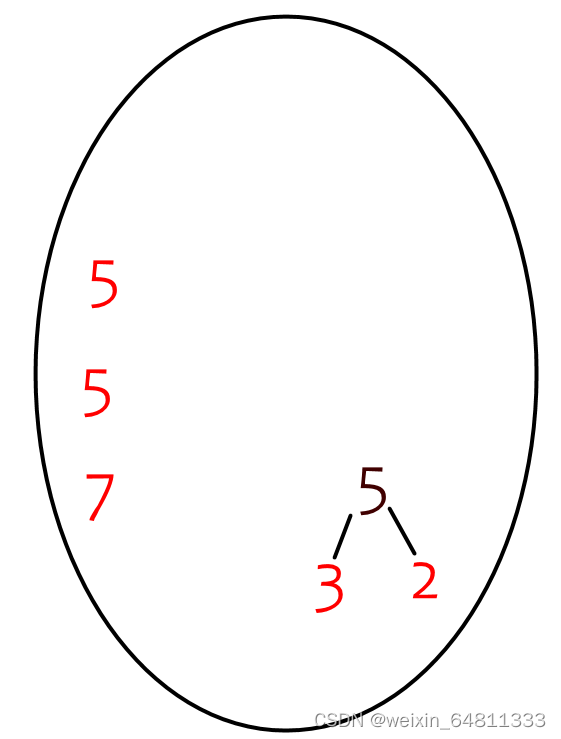
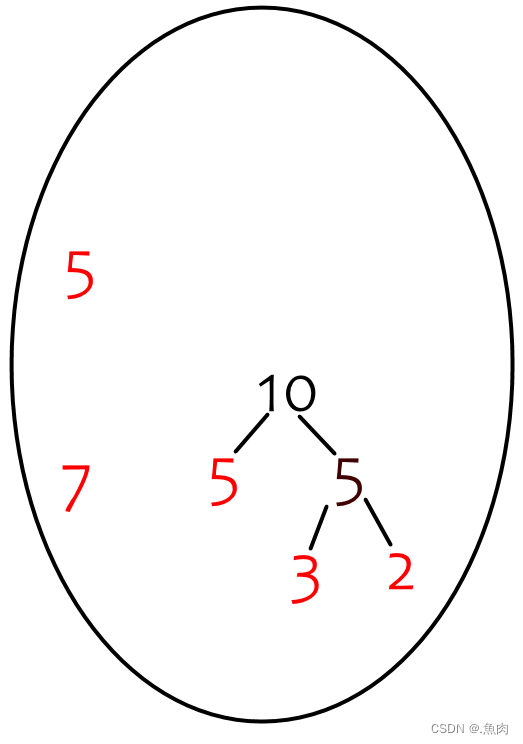
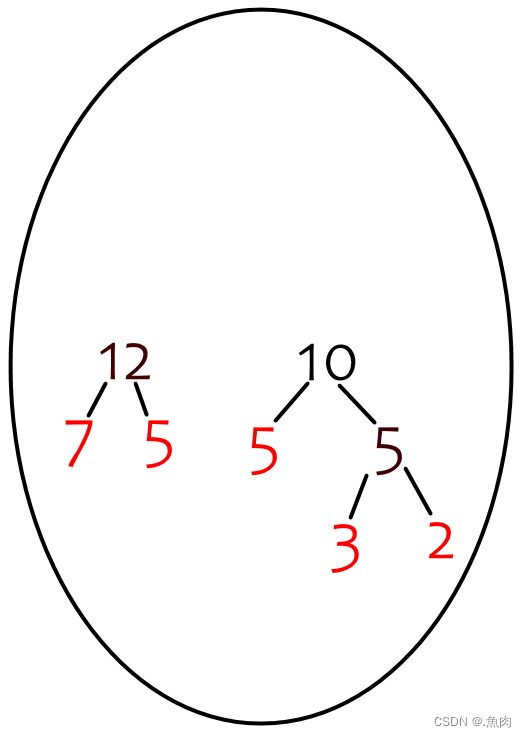
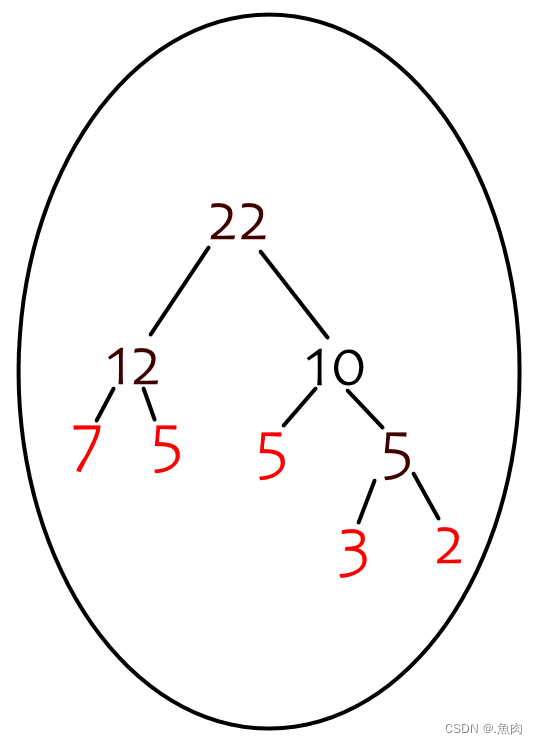
 求Huffman树的带权路径长度算法：

书上讲常见的求Huffman树的带权路径长度算法为：从叶子结点权值乘路径长度：

WPL=7*2+5*2+5*2+3*3+2*3=49

另外一种求WPL的算法为：非叶子几点权值之和：

WPL=22+12+10+5=49

这种方法并不是毫无道理，应为同一个结点下的两个叶子结点的路径长度是一样的，叶子结点的路径长度完全可以反映到其双亲结点上去。

这种算法较为简单，直接可以忽略建树的步骤，直接求出WPL（当然要明白如何求WPL）

算法的主要思想：

1.首先将得到的元素集合进行排序；（降序。升序也行，请自己尝试）

2.数组末尾两个元素求和（俩结点的双亲结点权值），将其结果放在数组倒数第二个位置上并且数组长度减1

3.累加每次求和结果。（即就是非叶子结点的权值）

注意：当集合元素过小时不适用本算法，需要特殊处理，不然会发生数组越界。

C语言实现：

#include<stdio.h>
#include<malloc.h>
// 算法思想：
// 本题主要为求哈夫曼树的带权路径长度，故未将重点放在建树上
// Huffman树的带权路径长其实就是其非叶子结点的权值和//排序算法
void sort(int *data,int n){int i,j;for(i =0;i<n;++i){for (j = 0;  j< n-i; ++j) {if(data[j]<data[j+1]){int t = data[j+1];data[j+1] = data[j];data[j] = t;}}}
}int main() {int n, *data,i,sum =0,x;scanf("%d", &n);//动态开辟数组data = (int *) malloc(sizeof(int)*n);for(i =0;i<n;++i)scanf("%d",&data[i]);if(n<=2){   //当集合过小时，不适用本算法,特殊处理for(i =0;i<n;++i)sum += data[i];printf("%d",data[0]+data[1]);return 0;}while(1){sort(data,n);   //先对数组排序（降序）x=data[n-1]+data[n-2];  //将末尾两元素求和（上层结点权值）data[n-2] = x;  //消除原来两元素，增加新元素sum+=x; //累计非叶子结点权值和--n;    //数组长度减1if(n==1)    //当数组中只剩下一个元素时，得出结果break;}printf("%d\n",sum);
}

运行测试：