觉得有帮助或需要源码请点赞关注收藏后评论区留言或私信博主要
在强化学习中,动态规划法主要用于求解有模型的MDP问题,尽管在现实任务中难以获得完备的环境模型,且动态规划法需要消耗大量的计算资源,但是作为强化学习的基础,动态规划法仍然具有非常重要的理论意义。
动态规划法主要包括基于模型的策略迭代和基于模型的值迭代两种。这两种算法都是利用值函数来评价策略的,一旦计算出满足贝尔曼最优方程的最优状态值函数V或最优动作值函数Q,就能得到最优策略。
策略迭代通过构建策略的值函数(状态值函数v 动作值函数q)来评估当前策略,并利用这些值函数给出改进的新策略,策略跌打由策略评估和策略改进两部分组成。
下面通过扫地机器人在不同环境下的策略评估进行实战
基于状态值函数的策略评估

1:确定环境如下
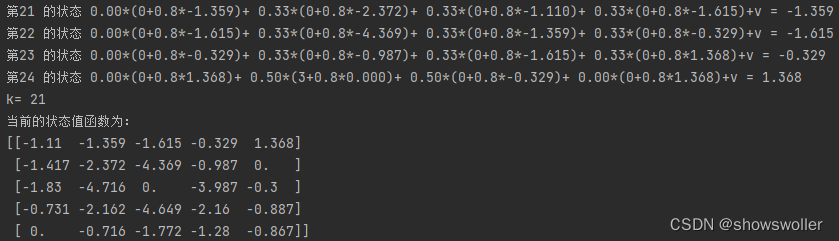
部分代码如下
# 代05-例4.1-基于状态值函数的确定环境扫地机器人任务策略评估
import numpy as npfrom 扫地机器人gym环境 import GridWorldEnvenv = GridWorldEnv()
"""定义格子世界参数"""
world_h = 5
world_w = 5
length = world_h * world_w
gamma = 0.8
state = [i for i in range(length)] # 状态(编号)
action = ['n', 's', 'w', 'e'] # 动作名称
ds_action = {'n': -world_w, 'e': 1, 's': world_w, 'w': -1}
policy = np.zeros([length, len(action)])
suqe=[20, 21, 22, 23, 24, 15, 16, 17, 18, 19, 10, 11, 12, 13, 14, 5, 6, 7, 8, 9, 0, 1, 2, 3,4]# 定义奖励
def reward(s):if s == 20: # 到充电站return 1elif s == 12: # 到陷阱中return -10elif s == 9: # 到垃圾处return 3else:return 0 # 其他def getAction(a):if a == 'n':return 0elif a == 'e':return 3elif a == 's':return 1elif a == 'w':return 2
入状态,则直接pass不做操作continuev = 0 # 针对每个状态值函数进行计算print("第%d 的状态" % (k), end="")for a in action:newAction = getAction(a)next_state = next_states(s, a)rewards = reward(next_state)if next_state == 12:v += policy[s][newAction] * (rewards + gamma * V[s])# print(" %.2f*(%d+%.1f*%.3f)+" % (policy[s][newAction], rewards, gamma, V[next_state]), end="")print(" %.2f*(%d+%.1f*%.3f)+" % (policy[s][newAction], rewards, gamma, V[next_state]), end="")else:v += policy[s][newAction] * (rewards + gamma * V[next_state])# print("%.2f*(%d+%.1f*%.2f)+" % (policy[s][newAction], rewards, gamma, value[next_state]), end="")# print()# successor = getsuccessor(s)# for next_state in successor:# rewards = reward(next_state)# v += 1 / len(successor) * (rewards + gamma * V[next_state])print(" %.2f*(%d+%.1f*%.3f)+" % (policy[s][newAction], rewards, gamma, V[next_state]), end="")print("v = %.3f" % (v))delta = max(delta, np.abs(v - V[s])) # 更新差值V[s] = v # 存储(更新)每个状态下的状态值函数,即伪代码中的 v <- V(s)value = np.array(V).reshape(world_h, world_w)iter += 1print('k=', iter) # 打印迭代次数print("当前的状态值函数为:")print(np.round(value, decimals=3))# 输出当前的状态值函数if delta < theta: # 策略评估的迭代次数不能太多,否则状态值函数的数值会越来越大(即使算法仍然在收敛)breakreturn V # 一轮迭代结束后,状态值函数暂时固定initPolicy()
value = policy_eval()随机环境的状态值函数策略评估此处省略 有需要请点赞关注收藏后私信博主
基于动作值函数的策略评估

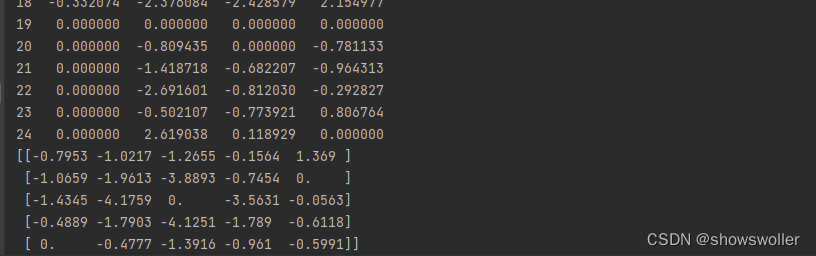
部分代码如下
# 代08-例4.4-基于动作值函数的随机环境扫地机器人任务策略评估
import numpy as np
import pandas as pd"""定义格子世界参数"""
world_h = 5
world_w = 5
length = world_h * world_w
gamma = 0.8
action = ['n', 's', 'w', 'e'] # 动作名称
ds_action = {'n': -world_w, 'e': 1, 's': world_w, 'w': -1}
policy = np.zeros([length, len(action)])
suqe=[20, 21, 22, 23, 24, 15, 16, 17, 18, 19, 10, 11, 12, 13, 14, 5, 6, 7, 8, 9, 0, 1, 2, 3,4]# 定义奖励
def reward(s):if s == 20: # 到充电站return 1elif s == 12: # 到陷阱中return -10elif s == 9: # 到垃圾处return 3else:return 0 # 其他# in表示0是[*,*,*]中的一个def getAction(a):if a == 'n':return 0elif a == 'e':return 3elif a == 's':return 1elif a == 'w':return 2# 在s状态下执行动作a,返回下一状态(编号)
def next_states(s, a):# 越过边界时passif (s < world_w and a == 'n') \or (s % world_w == 0 and a == 'w') \or (s > length - world_w - 1 and a == 's') \or ((s + 1) % world_w == 0 and a == 'e'): # (s % (world_w - 1) == 0 and a == 'e' and s != 0)next_state = s # 表现为next_state不变else:next_state = s + ds_action[a] # 进入下一个状态return next_state# 在s状态下执行动作,返回所有可能的下一状态(编号)list
def getsuccessor(s):successor = []for a in action: # 遍历四个动作if s == next_states(s, a):continueelse:# print("状态s=%s,动作a=%s"%(s,a))next = next_states(s, a) # 得到下一个状态(编号)successor.append(next) # 以list保存当前状态s下执行四个动作的下一状态# print(len(successor))return successordef envActionPolicy(a):if a == 'n':return 's'elif a == 's':return 'n'elif a == 'e':return 'w'elif a == 'w':return 'e'def CaValue(Q):v = [0 for i in range(length)]for i in range(length):for a in action:newAction = getAction(a)v[i] += policy[i][newAction] * Q.loc[i, a]value = np.array(v).reshape(world_h, world_w)print(np.round(value, decimals=4))def sumQ_nextstate(s, Q, visios):sum = 0for i in action:newAction = getAction(i)sum += policy[s][newAction] * Q.loc[s, i]return sumdef initPolicy():for s in range(length):for a in action:if next_states(s, a) == s:continuenewAction = getAction(a)policy[s][newAction] = 1 / len(getsuccessor(s))# print(policy)
def policy_eval_Q_random(theta=0.0001):Q = pd.DataFrame(np.zeros((length, len(action))), # q_table initial valuescolumns=action, # actions's name)iter = 0while True:k = -1delta = 0 # 定义最大差值,判断是否有进行更新for s in suqe: # 遍历所有状态 [0~25]visio = Falsek += 1if s in [9, 20, 12]: # 若当前状态为吸入状态,则直接pass不做操作continueif s == 17:visio = True# [[-0.7954 - 1.0218 - 1.2655 - 0.1564 1.369]# [-1.066 - 1.9614 - 3.8893 - 0.7455 0.]# [-1.4346 - 4.176# 0. - 3.5631 - 0.0563]# [-0.489 - 1.7904 - 4.1252 - 1.7891 - 0.6118]# [0. - 0.4778 - 1.3917 - 0.9611 - 0.5992]]for a in action:newAction = getAction(a)env_action = envActionPolicy(a)next_state = next_states(s, a)env_state = next_states(s, env_action)rewards = reward(next_state)env_rewards = reward(env_state)if policy[s][newAction] == 0:continueif next_state == 12:q = 0.8 * (rewards + gamma * sumQ_nextstate(s, Q, visio)) + 0.15 * (gamma * sumQ_nextstate(s, Q, visio)) + 0.05 * (env_rewards + gamma * (sumQ_nextstate(env_state, Q, visio)))if visio == True:print("q=%.2f=0.8*(%.2f+%.2f*%.2f)+0.15*(%.2f*%.2f)+0.05*(%.2f+%.2f*%.2f)"% (q, rewards, gamma, sumQ_nextstate(s, Q, visio), gamma, sumQ_nextstate(s, Q, visio),env_rewards, gamma, sumQ_nextstate(env_state, Q, visio)))else:q = 0.8 * (rewards + gamma * sumQ_nextstate(next_state, Q, visio)) + 0.05 * (env_rewards + gamma * sumQ_nextstate(env_state, Q, visio)) \+ 0.15 * gamma * sumQ_nextstate(s, Q, visio)if visio == True:print("q=%.2f=0.8*(%.2f+%.2f*%.2f)+0.15*(%.2f*%.2f)+0.05*(%.2f+%.2f*%.2f)" % (q,rewards, gamma,sumQ_nextstate(next_state, Q,visio), gamma,sumQ_nextstate(s,Q,visio),env_rewards,gamma,sumQ_nextstate(env_state, Q,visio)))delta = max(delta, np.abs(q - Q.loc[s, a])) # 更新差值Q.loc[s, a] = q # 存储(更新)每个状态下的状态值函数,即伪代码中的 v <- V(s)iter += 1print('k=', iter) # 打印迭代次数k = 0Q1 = pd.DataFrame(np.zeros((length, len(action))), # q_table initial valuescolumns=action, # actions's name)for s in suqe:Q1.loc[k] = Q.loc[s]k = k + 1Q1.rename(columns={'n': 'UP', 's': 'DOWN', 'w': 'LEFT', 'e': 'RIGHT'}, inplace=True)print(Q1)if delta < theta: # 策略评估的迭代次数不能太多,否则状态值函数的数值会越来越大(即使算法仍然在收敛)break# CaValue(Q)return QinitPolicy()
q = policy_eval_Q_random()
CaValue(q)确定环境下的省略不表 有需要请点赞关注收藏后私信博主要