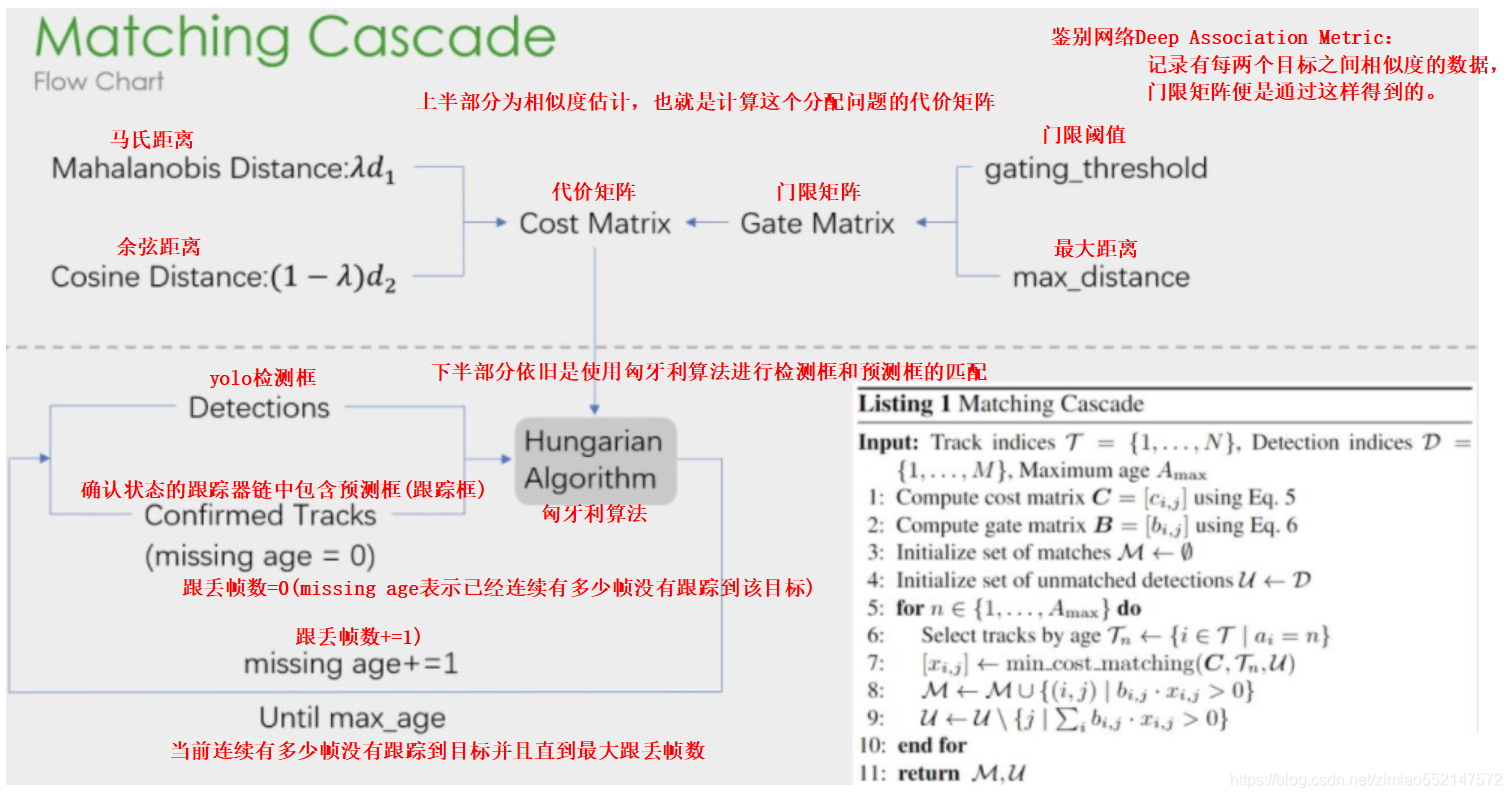
MPC控制简介

众所周知，控制算法中，PID的应用占据了90％，而另外10％就是这次的主角MPC控制算法。
MPC控制算法全称模型预测控制，它相对比PID有着多输入，多输出以及更加平稳的特点。并且最重要的是，MPC可以针对非线性的系统进行控制。
由于其平稳的和非线性问题有着较强处理能力的特点，其在自动驾驶领域异常流行。

MPC全称：模型预测控制

1. 模型：即简单运动学模型，一般需要转化为线性的，离散的状态空间方程作为基本模型
2. 预测：根据模型预测未来数个时间段内（离散的）的状态
3. 控制：根据预测内容进行二次优化与处理，得出合适控制量。

简单流程（个人简单理解，若有误请指出）

车辆运动学模型

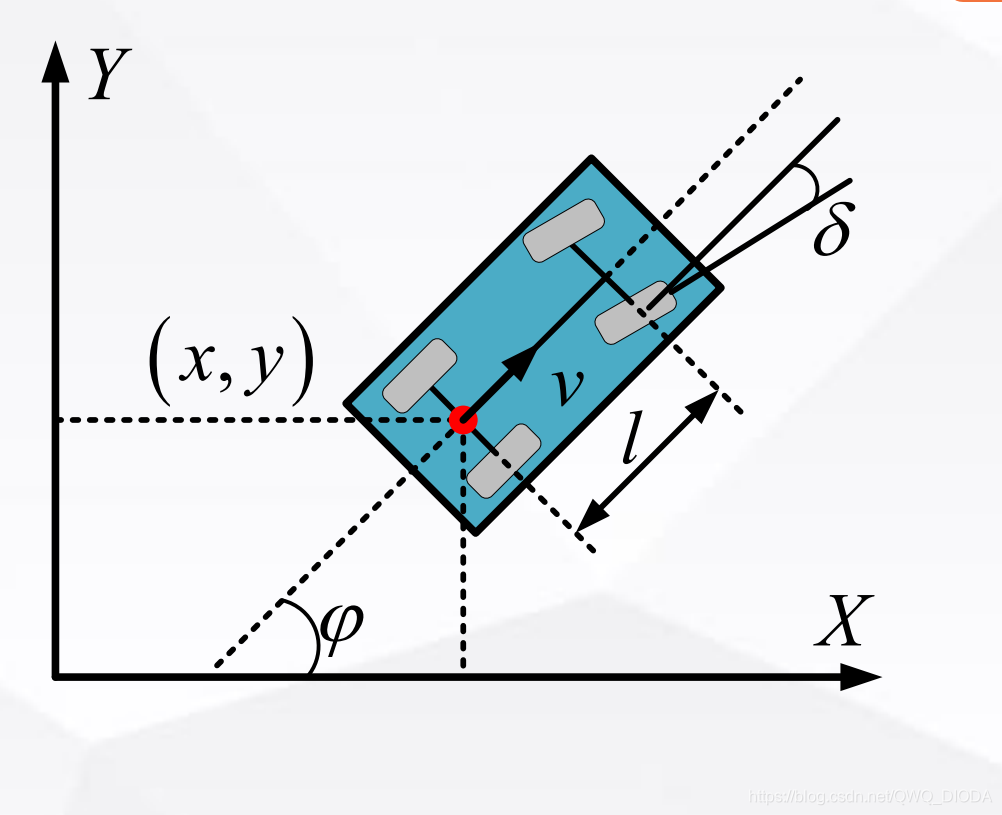
公式为

$$\begin{gathered} x^{\prime }=v\ast \cos (\phi ). \\ {y}^{\prime }=v\ast \sin (\phi ). \\ {x}^{\prime }=\frac{v\ast \tan (\delta )}{l}. \end{gathered}$$

由于MPC的模型需要、状态空间方程、线性的、离散的表达
因此第一步就是使其成为状态空间方程

完整的表示一个车的状态，我们需要用到他的坐标和角度也就是[x,y,φ]
车辆是一个二自由度模型。控制量分别是：后轮的速度v，前轮的转角δ.

于此，可以确定
$$状态量X=\left[\begin{array}{c}x\\ y\\ \phi \end{array}\right]$$
$$控制量U=\left[\begin{array}{c}v\\ \delta \end{array}\right]$$
$$\begin{gathered} 状态空间方程 \\ \text{X˙}=f(X,U) \end{gathered}$$
后对状态空间方程进行一阶泰勒展开（线性化）
首先设置参考点（通常为规划好的路径中的参考点）
$$参考点\text{Xr˙}=f(Xr,Ur)$$
$$\begin{gathered} 泰勒展开： \\ \text{X˙}=f(Xr,Ur)+\frac{\delta f(X,U)}{\delta X}\ast (X-Xr)+\frac{\delta f(X,U)}{\delta U}\ast (U-Ur). \end{gathered}$$
由于仍存在无法求得的f(Xr,Ur)，因此我们转换策略，改为状态误差量
$$\begin{gathered} 泰勒展开： \\ \text{X˜˙}=\text{X˙}-\text{X˙r}=\frac{\delta f(X,U)}{\delta X}\ast (X-Xr)+\frac{\delta f(X,U)}{\delta U}\ast (U-Ur). \end{gathered}$$
$$\begin{gathered} \text{X˜}=X-Xr \\ \text{U˜}=U-Ur \end{gathered}$$
如此便可以得到
$$\frac{\delta f(X,U)}{\delta X}=A，\frac{\delta f(X,U)}{\delta U}=B.$$
$$\text{X˜˙}=A\ast \text{X˜}+B\ast \text{U˜}$$
即线性化完毕
线性化完毕后，由于计算机程序是离散的，因此我们需要将其离散化
$$\frac{\text{X˜}(k+1)-\text{X˜}(k)}{T}=A\ast \text{X˜}(k)+B\ast \text{U˜}(k)$$
为此可以转化为
$$\text{X˜}(k+1)=a\ast \text{X˜}(k)+b\ast \text{U˜}(k)$$
又因为控制量是没有参考值的，所以在此使用误差是不合适的，因此可以将控制量转变为控制增量
转变过程则是根据已经离散化和线性化好的状态空间方程进行改变。
也就是说我们可以设计一个新的的空间状态方程，将之前整理好的状态空间方程输出的作为状态量，控制增量作为控制量，并进行推导
推导流程（图片来源，b站up：小黎的Ally，侵删）

最后一步的输出方程，含义为：
最终预测结果只输出[x,y,φ]等真正的状态量。

预测

根据模型所得得最终得状态空间和输出方程我们就可以对模型进行预测
也就是
$$\begin{gathered} \xi (k+1)=A\xi (k)+B\Delta \text{u˜}(k) \\ \xi (k+2)=A\xi (k+1)+B\Delta \text{u˜}(k+1) \\ \xi (k+3)=A\xi (k+2)+B\Delta \text{u˜}(k+2) \\ ... \\ \xi (k+Nc+1)=A\xi (k+Nc)+B\Delta \text{u˜}(k+Nc) \\ ... \\ \xi (k+Np+1)=A\xi (k+Np)+B\Delta \text{u˜}(k+Np) \end{gathered}$$
这里
预测时域Np和控制时域Nc。

预测时域很好理解，简单来说就是程序中预测多少个时刻的状态。

控制时域是我们可控制未来多少步。

将第一个预测公式逐步代入到下方公式并将公式乘以C(转化为输出方程)

即为（暂且忽视红圈）

未来状态的输出量 = 当前的状态量 * 系数矩阵 + （从当前时刻到未来时刻的控制量）
在上面的公式中有个问题，就是未来要预测几个矩阵？，未来预测到什么时候结束控制量的累加？

这两个问题就是对应了预测时域Np和控制时域Nc。
这个时域我们一般自定。

最后观看政个算式，可以将其变化为矩阵运算

红圈部分即为预测出的算式，这个Y就是最终预测的未来时刻的状态矩阵。

控制

根据我们预测方程，最终得出状态量与参考量的误差，因此需要输出的状态量（误差）绝对值最小，又因为Y是一个矩阵，所以我们就需要使该矩阵得平方最小。

$$Jmin=Y^{\prime }\ast Y$$
同时，我们有需要尽量平滑的抵达目标位置，如何平滑呐？也就是控制量（此处为控制增量）绝对值保持最小！
$$Jmin=\Delta U^{\prime }\ast \Delta U$$

最后对快速抵达目标的目的和平滑的目的取一个权重。
$$Jmin=Y^{\prime }QY+\Delta U^{\prime }R\Delta U$$
Q大的化就代表更偏向快速到目标位置（但是会增大震荡），R大就代表到达目标位置更平稳（但是响应慢）。
其中国Q必须是行数和Y'相等，列数和Y相等的N倍单位矩阵（N为自定大小）

MPC的控制总的来说是一次二次规划问题。
也就是说，他应该长这样。

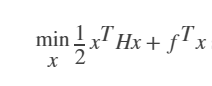
但是我们这里面却有两个自变量。。。。。把预测中Y等号右边的算式带入整理，去掉常数项可得

这样，结果就成为了一个二次规划问题。

当然，还有ΔU和U的限制问题，需要自己根据自己车辆参数设计。

之后利用matlab的二次规划工具箱结算出ΔU矩阵。matlab quadprog函数使用.
注意：计算出的是一个（Nc*控制量个数）长的向量，且是控制增量！

最后，我们只需将计算出的第一组控制增量加到目前的控制量中即可。

滚动优化

控制量作用于系统，并在下一刻得出系统状态在进行一次预测与二次优化即可。