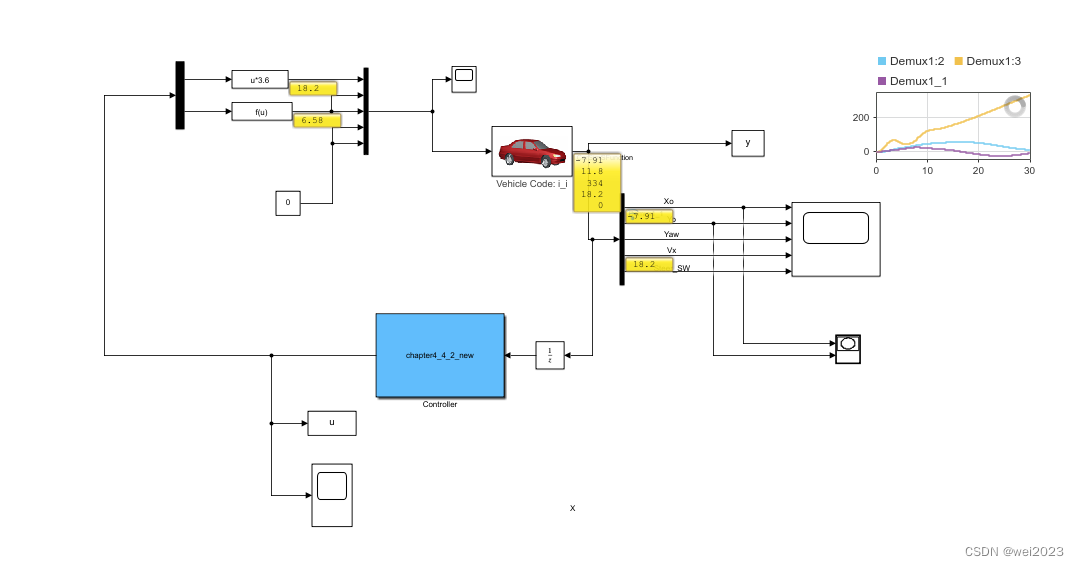
学习北理工的无人驾驶车辆模型预测控制第2版第四章,使用的仿真软件为Carsim8和MatlabR2019a联合仿真,使用MPC控制思想对车辆进行轨迹跟踪控制,并给出仿真结果。
mpc控制器函数:s-function
function [sys,x0,str,ts] = MY_MPCController3(t,x,u,flag)
% 该函数是写的第3个S函数控制器(MATLAB版本:R2011a)
% 限定于车辆运动学模型,控制量为速度和前轮偏角,使用的QP为新版本的QP解法
% [sys,x0,str,ts] = MY_MPCController3(t,x,u,flag)
%
% is an S-function implementing the MPC controller intended for use
% with Simulink. The argument md, which is the only user supplied
% argument, contains the data structures needed by the controller. The
% input to the S-function block is a vector signal consisting of the
% measured outputs and the reference values for the controlled
% outputs. The output of the S-function block is a vector signal
% consisting of the control variables and the estimated state vector,
% potentially including estimated disturbance states.switch flag,case 0[sys,x0,str,ts] = mdlInitializeSizes; % Initializationcase 2sys = mdlUpdates(t,x,u); % Update discrete statescase 3sys = mdlOutputs(t,x,u); % Calculate outputscase {1,4,9} % Unused flagssys = [];otherwiseerror(['unhandled flag = ',num2str(flag)]); % Error handling
end
% End of dsfunc.%==============================================================
% Initialization
%==============================================================function [sys,x0,str,ts] = mdlInitializeSizes% Call simsizes for a sizes structure, fill it in, and convert it
% to a sizes array.sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 3; % this parameter doesn't matter
sizes.NumOutputs = 2; %[speed, steering]
sizes.NumInputs = 5; %[x,y,yaw,vx,steer_sw]
sizes.DirFeedthrough = 1; % Matrix D is non-empty.
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 =[0;0;0];
global U; % store current ctrl vector:[vel_m, delta_m]
U=[0;0];
% Initialize the discrete states.
str = []; % Set str to an empty matrix.
ts = [0.05 0]; % sample time: [period, offset]
%End of mdlInitializeSizes%==============================================================
% Update the discrete states
%==============================================================
function sys = mdlUpdates(t,x,u)sys = x;
%End of mdlUpdate.%==============================================================
% Calculate outputs
%==============================================================function sys = mdlOutputs(t,x,u)
global a b u_piao;
%u_piao矩阵,用于存储每一个仿真时刻,车辆的实际控制量(实际运动状态)与目标控制量(运动状态)之间的偏差global U; %store chi_tilde=[vel-vel_ref; delta - delta_ref]
global kesi;tic
Nx=3;%状态量的个数
Nu =2;%控制量的个数
Np =60;%预测步长
Nc=30;%控制步长
Row=10;%松弛因子
fprintf('Update start, t=%6.3f\n',t)
t_d =u(3)*3.1415926/180;%CarSim输出的Yaw angle为角度,角度转换为弧度% %直线路径
% r(1)=5*t; %ref_x-axis
% r(2)=5;%ref_y-axis
% r(3)=0;%ref_heading_angle
% vd1=5;% ref_velocity
% vd2=0;% ref_steering% % 半径为25m的圆形轨迹, 圆心为(0, 35), 速度为5m/sr(1)=25*sin(0.2*t);r(2)=35-25*cos(0.2*t);r(3)=0.2*t;vd1=5;vd2=0.104;% %半径为35m的圆形轨迹, 圆心为(0, 35), 速度为3m/s
% r(1)=25*sin(0.12*t);
% r(2)=25+10-25*cos(0.12*t);
% r(3)=0.12*t;
% vd1=3;
% vd2=0.104;
%半径为25m的圆形轨迹, 圆心为(0, 35), 速度为10m/s
% r(1)=25*sin(0.4*t);
% r(2)=25+10-25*cos(0.4*t);
% r(3)=0.4*t;
% vd1=10;
% vd2=0.104;
%半径为25m的圆形轨迹, 圆心为(0, 35), 速度为4m/s
% r(1)=25*sin(0.16*t);
% r(2)=25+10-25*cos(0.16*t);
% r(3)=0.16*t;
% vd1=4;
% vd2=0.104;% t_d = r(3);
kesi=zeros(Nx+Nu,1);
kesi(1) = u(1)-r(1);%u(1)==X(1),x_offset
kesi(2) = u(2)-r(2);%u(2)==X(2),y_offset
heading_offset = t_d - r(3); %u(3)==X(3),heading_angle_offsetif (heading_offset < -pi)heading_offset = heading_offset + 2*pi;
end
if (heading_offset > pi)heading_offset = heading_offset - 2*pi;
end
kesi(3)=heading_offset;% U(1) = u(4)/3.6 - vd1; % vel, km/h-->m/s
% steer_SW = u(5)*pi/180;
% steering_angle = steer_SW/18.0;
% U(2) = steering_angle - vd2;kesi(4)=U(1); % vel-vel_ref
kesi(5)=U(2); % steer_angle - steering_ref
fprintf('vel-offset=%4.2f, steering-offset, U(2)=%4.2f\n',U(1), U(2))T=0.05;
T_all=40;%临时设定,总的仿真时间,主要功能是防止计算期望轨迹越界
% Mobile Robot Parameters
L = 2.6; % wheelbase of carsim vehicle
% Mobile Robot variable%矩阵初始化
u_piao=zeros(Nx,Nu);
Q=eye(Nx*Np,Nx*Np);
R=5*eye(Nu*Nc);
a=[1 0 -vd1*sin(t_d)*T;0 1 vd1*cos(t_d)*T;0 0 1;];
b=[cos(t_d)*T 0;sin(t_d)*T 0;tan(vd2)*T/L vd1*T/(cos(vd2)^2)];A_cell=cell(2,2);
B_cell=cell(2,1);
A_cell{1,1}=a;
A_cell{1,2}=b;
A_cell{2,1}=zeros(Nu,Nx);
A_cell{2,2}=eye(Nu);
B_cell{1,1}=b;
B_cell{2,1}=eye(Nu);A=cell2mat(A_cell);
B=cell2mat(B_cell);
C=[ 1 0 0 0 0;0 1 0 0 0;0 0 1 0 0];PHI_cell=cell(Np,1);
THETA_cell=cell(Np,Nc);
for j=1:1:NpPHI_cell{j,1}=C*A^j;for k=1:1:Ncif k<=jTHETA_cell{j,k}=C*A^(j-k)*B;elseTHETA_cell{j,k}=zeros(Nx,Nu);endend
end
PHI=cell2mat(PHI_cell);%size(PHI)=[Nx*Np Nx+Nu]
THETA=cell2mat(THETA_cell);%size(THETA)=[Nx*Np Nu*(Nc+1)]H_cell=cell(2,2);
H_cell{1,1}=THETA'*Q*THETA+R;
H_cell{1,2}=zeros(Nu*Nc,1);
H_cell{2,1}=zeros(1,Nu*Nc);
H_cell{2,2}=Row;
H=cell2mat(H_cell);
% H=(H+H')/2;error=PHI*kesi;
f_cell=cell(1,2);
f_cell{1,1} = (error'*Q*THETA);
f_cell{1,2} = 0;
f=cell2mat(f_cell);%% 以下为约束生成区域
%不等式约束
A_t=zeros(Nc,Nc);%见falcone论文 P181
for p=1:1:Ncfor q=1:1:Ncif q<=pA_t(p,q)=1;elseA_t(p,q)=0;endend
end
A_I=kron(A_t,eye(Nu));%对应于falcone论文约束处理的矩阵A,求克罗内克积
Ut=kron(ones(Nc,1), U);%
umin=[-0.2; -0.54];%[min_vel, min_steer]维数与控制变量的个数相同
umax=[0.05; 0.436]; %[max_vel, max_steer],%0.436rad = 25deg
delta_umin = [-0.5; -0.0082]; % 0.0082rad = 0.47deg
delta_umax = [0.5; 0.0082];Umin=kron(ones(Nc,1),umin);
Umax=kron(ones(Nc,1),umax);
A_cons_cell={A_I zeros(Nu*Nc, 1); -A_I zeros(Nu*Nc, 1)};
b_cons_cell={Umax-Ut;-Umin+Ut};
A_cons=cell2mat(A_cons_cell);%(求解方程)状态量不等式约束增益矩阵,转换为绝对值的取值范围
b_cons=cell2mat(b_cons_cell);%(求解方程)状态量不等式约束的取值% 状态量约束
delta_Umin = kron(ones(Nc,1),delta_umin);
delta_Umax = kron(ones(Nc,1),delta_umax);
lb = [delta_Umin; 0];%(求解方程)状态量下界
ub = [delta_Umax; 10];%(求解方程)状态量上界%% 开始求解过程
% options = optimset('Algorithm','active-set');
options = optimset('Algorithm','interior-point-convex');
warning off all % close the warnings during computation
[X, fval,exitflag]=quadprog(H, f, A_cons, b_cons,[], [],lb,ub,[],options);fprintf('quadprog EXITFLAG = %d\n',exitflag);%% 计算输出
if ~isempty(X)u_piao(1)=X(1);u_piao(2)=X(2);
end;
U(1)=kesi(4)+u_piao(1);%用于存储上一个时刻的控制量
U(2)=kesi(5)+u_piao(2);
u_real(1) = U(1) + vd1;
u_real(2) = U(2) + vd2;sys=u_real % vel, steering, x, y
toc
% End of mdlOutputs.新版的matlab没有active-set算法,需要更改为'interior-point-convex',但是会出现X出差索引范围,需要采用旧版的quadprog函数算法,这里更改为quadprog2011,具体代码如下;
function [X,fval,exitflag,output,lambda] = quadprog2011(H,f,A,B,Aeq,Beq,lb,ub,X0,options,varargin)
%QUADPROG Quadratic programming.
% X = QUADPROG(H,f,A,b) attempts to solve the quadratic programming
% problem:
%
% min 0.5*x'*H*x + f'*x subject to: A*x <= b
% x
%
% X = QUADPROG(H,f,A,b,Aeq,beq) solves the problem above while
% additionally satisfying the equality constraints Aeq*x = beq.
%
% X = QUADPROG(H,f,A,b,Aeq,beq,LB,UB) defines a set of lower and upper
% bounds on the design variables, X, so that the solution is in the
% range LB <= X <= UB. Use empty matrices for LB and UB if no bounds
% exist. Set LB(i) = -Inf if X(i) is unbounded below; set UB(i) = Inf if
% X(i) is unbounded above.
%
% X = QUADPROG(H,f,A,b,Aeq,beq,LB,UB,X0) sets the starting point to X0.
%
% X = QUADPROG(H,f,A,b,Aeq,beq,LB,UB,X0,OPTIONS) minimizes with the
% default optimization parameters replaced by values in the structure
% OPTIONS, an argument created with the OPTIMSET function. See OPTIMSET
% for details. Used options are Display, Diagnostics, TolX, TolFun,
% HessMult, LargeScale, MaxIter, PrecondBandWidth, TypicalX, TolPCG, and
% MaxPCGIter. Currently, only 'final' and 'off' are valid values for the
% parameter Display ('iter' is not available).
%
% X = QUADPROG(PROBLEM) finds the minimum for PROBLEM. PROBLEM is a
% structure with matrix 'H' in PROBLEM.H, the vector 'f' in PROBLEM.f,
% the linear inequality constraints in PROBLEM.Aineq and PROBLEM.bineq,
% the linear equality constraints in PROBLEM.Aeq and PROBLEM.beq, the
% lower bounds in PROBLEM.lb, the upper bounds in PROBLEM.ub, the start
% point in PROBLEM.x0, the options structure in PROBLEM.options, and
% solver name 'quadprog' in PROBLEM.solver. Use this syntax to solve at
% the command line a problem exported from OPTIMTOOL. The structure
% PROBLEM must have all the fields.
%
% [X,FVAL] = QUADPROG(H,f,A,b) returns the value of the objective
% function at X: FVAL = 0.5*X'*H*X + f'*X.
%
% [X,FVAL,EXITFLAG] = QUADPROG(H,f,A,b) returns an EXITFLAG that
% describes the exit condition of QUADPROG. Possible values of EXITFLAG
% and the corresponding exit conditions are
%
% All algorithms:
% 1 First order optimality conditions satisfied.
% 0 Maximum number of iterations exceeded.
% -2 No feasible point found.
% -3 Problem is unbounded.
% Interior-point-convex only:
% -6 Non-convex problem detected.
% Trust-region-reflective only:
% 3 Change in objective function too small.
% -4 Current search direction is not a descent direction; no further
% progress can be made.
% Active-set only:
% 4 Local minimizer found.
% -7 Magnitude of search direction became too small; no further
% progress can be made. The problem is ill-posed or badly
% conditioned.
%
% [X,FVAL,EXITFLAG,OUTPUT] = QUADPROG(H,f,A,b) returns a structure
% OUTPUT with the number of iterations taken in OUTPUT.iterations,
% maximum of constraint violations in OUTPUT.constrviolation, the
% type of algorithm used in OUTPUT.algorithm, the number of conjugate
% gradient iterations (if used) in OUTPUT.cgiterations, a measure of
% first order optimality (large-scale algorithm only) in
% OUTPUT.firstorderopt, and the exit message in OUTPUT.message.
%
% [X,FVAL,EXITFLAG,OUTPUT,LAMBDA] = QUADPROG(H,f,A,b) returns the set of
% Lagrangian multipliers LAMBDA, at the solution: LAMBDA.ineqlin for the
% linear inequalities A, LAMBDA.eqlin for the linear equalities Aeq,
% LAMBDA.lower for LB, and LAMBDA.upper for UB.
%
% See also LINPROG, LSQLIN.% Copyright 1990-2010 The MathWorks, Inc.
% $Revision: 1.1.6.14 $ $Date: 2010/11/01 19:41:32 $defaultopt = struct( ...'Algorithm','trust-region-reflective', ...'Diagnostics','off', ...'Display','final', ...'HessMult',[], ... 'LargeScale','on', ...'MaxIter',[], ... 'MaxPCGIter','max(1,floor(numberOfVariables/2))', ... 'PrecondBandWidth',0, ... 'TolCon',1e-8, ...'TolFun',[], ...'TolPCG',0.1, ... 'TolX',100*eps, ...'TypicalX','ones(numberOfVariables,1)' ... );% If just 'defaults' passed in, return the default options in X
if nargin == 1 && nargout <= 1 && isequal(H,'defaults')X = defaultopt;return
endif nargin < 10options = [];if nargin < 9X0 = [];if nargin < 8ub = [];if nargin < 7lb = [];if nargin < 6Beq = [];if nargin < 5Aeq = [];if nargin < 4B = [];if nargin < 3A = [];endendendendendendend
end% Detect problem structure input
if nargin == 1if isa(H,'struct')[H,f,A,B,Aeq,Beq,lb,ub,X0,options] = separateOptimStruct(H);else % Single input and non-structure.error(message('optim:quadprog:InputArg'));end
endif nargin == 0 error(message('optim:quadprog:NotEnoughInputs'))
end% Check for non-double inputs
% SUPERIORFLOAT errors when superior input is neither single nor double;
% We use try-catch to override SUPERIORFLOAT's error message when input
% data type is integer.
trydataType = superiorfloat(H,f,A,B,Aeq,Beq,lb,ub,X0);
catch MEif strcmp(ME.identifier,'MATLAB:datatypes:superiorfloat')dataType = 'notDouble';end
endif ~strcmp(dataType,'double')error(message('optim:quadprog:NonDoubleInput'))
end% Set up constant strings
activeSet = 'active-set';
trustRegReflect = 'trust-region-reflective';
interiorPointConvex = 'interior-point-convex';if nargout > 4computeLambda = true;
else computeLambda = false;
end
if nargout > 3computeConstrViolation = true;computeFirstOrderOpt = true;
else computeConstrViolation = false;computeFirstOrderOpt = false;
end% Options setup
largescale = isequal(optimget(options,'LargeScale',defaultopt,'fast'),'on');
Algorithm = optimget(options,'Algorithm',defaultopt,'fast'); diagnostics = isequal(optimget(options,'Diagnostics',defaultopt,'fast'),'on');
display = optimget(options,'Display',defaultopt,'fast');
detailedExitMsg = ~isempty(strfind(display,'detailed'));
switch display
case {'off', 'none'}verbosity = 0;
case {'iter','iter-detailed'}verbosity = 2;
case {'final','final-detailed'}verbosity = 1;
case 'testing'verbosity = 3;
otherwiseverbosity = 1;
end% Determine algorithm user chose via options. (We need this now to set
% OUTPUT.algorithm in case of early termination due to inconsistent
% bounds.) This algorithm choice may be modified later when we check the
% problem type.
algChoiceOptsConflict = false;
if strcmpi(Algorithm,'active-set')output.algorithm = activeSet;
elseif strcmpi(Algorithm,'interior-point-convex')output.algorithm = interiorPointConvex;
elseif strcmpi(Algorithm,'trust-region-reflective')if largescaleoutput.algorithm = trustRegReflect;else% Conflicting options Algorithm='trust-region-reflective' and% LargeScale='off'. Choose active-set algorithm.algChoiceOptsConflict = true; % Warn later, not in case of early terminationoutput.algorithm = activeSet;end
elseerror(message('optim:quadprog:InvalidAlgorithm'));
end mtxmpy = optimget(options,'HessMult',defaultopt,'fast');
% Check for name clash
functionNameClashCheck('HessMult',mtxmpy,'hessMult_optimInternal','optim:quadprog:HessMultNameClash');
if isempty(mtxmpy)% Internal Hessian-multiply functionmtxmpy = @hessMult_optimInternal;usrSuppliedHessMult = false;
elseusrSuppliedHessMult = true;
end% Set the constraints up: defaults and check size
[nineqcstr,numberOfVariablesineq] = size(A);
[neqcstr,numberOfVariableseq] = size(Aeq);
if isa(H,'double') && ~usrSuppliedHessMult% H must be square and have the correct size nColsH = size(H,2);if nColsH ~= size(H,1)error(message('optim:quadprog:NonSquareHessian'));end
else % HessMult in effect, so H can be anythingnColsH = 0;
end% Check the number of variables. The check must account for any combination of these cases:
% * User provides HessMult
% * The problem is linear (H = zeros, or H = [])
% * The objective has no linear component (f = [])
% * There are no linear constraints (A,Aeq = [])
% * There are no, or partially specified, bounds
% * There is no X0
numberOfVariables = ...max([length(f),nColsH,numberOfVariablesineq,numberOfVariableseq]);if numberOfVariables == 0% If none of the problem quantities indicate the number of variables,% check X0, even though some algorithms do not use it.if isempty(X0)error(message('optim:quadprog:EmptyProblem'));else% With all other data empty, use the X0 input to determine% the number of variables.numberOfVariables = length(X0);end
endncstr = nineqcstr + neqcstr;if isempty(f)f = zeros(numberOfVariables,1);
else % Make sure that the number of rows/columns in H matches the length of% f under the following conditions:% * The Hessian is passed in explicitly (no HessMult)% * There is a non-empty Hessianif ~usrSuppliedHessMult && ~isempty(H)if length(f) ~= nColsHerror(message('optim:quadprog:MismatchObjCoefSize'));endend
end
if isempty(A)A = zeros(0,numberOfVariables);
end
if isempty(B)B = zeros(0,1);
end
if isempty(Aeq)Aeq = zeros(0,numberOfVariables);
end
if isempty(Beq)Beq = zeros(0,1);
end% Expect vectors
f = f(:);
B = B(:);
Beq = Beq(:);if ~isequal(length(B),nineqcstr)error(message('optim:quadprog:InvalidSizesOfAAndB'))
elseif ~isequal(length(Beq),neqcstr)error(message('optim:quadprog:InvalidSizesOfAeqAndBeq'))
elseif ~isequal(length(f),numberOfVariablesineq) && ~isempty(A)error(message('optim:quadprog:InvalidSizesOfAAndF'))
elseif ~isequal(length(f),numberOfVariableseq) && ~isempty(Aeq)error(message('optim:quadprog:InvalidSizesOfAeqAndf'))
end[X0,lb,ub,msg] = checkbounds(X0,lb,ub,numberOfVariables);
if ~isempty(msg)exitflag = -2;X=X0; fval = []; lambda = [];output.iterations = 0;output.constrviolation = [];output.algorithm = ''; % Not known at this stageoutput.firstorderopt = [];output.cgiterations = []; output.message = msg;if verbosity > 0disp(msg)endreturn
end% Check that all data is real
if ~(isreal(H) && isreal(A) && isreal(Aeq) && isreal(f) && ...isreal(B) && isreal(Beq) && isreal(lb) && isreal(ub) && isreal(X0))error(message('optim:quadprog:ComplexData'))
endcaller = 'quadprog';
% Check out H and make sure it isn't empty or all zeros
if isa(H,'double') && ~usrSuppliedHessMultif norm(H,'inf')==0 || isempty(H)% Really a lp problemwarning(message('optim:quadprog:NullHessian'))[X,fval,exitflag,output,lambda]=linprog(f,A,B,Aeq,Beq,lb,ub,X0,options);returnelse% Make sure it is symmetricif norm(H-H',inf) > epsif verbosity > -1warning(message('optim:quadprog:HessianNotSym'))endH = (H+H')*0.5;endend
end% Determine which algorithm and make sure problem matches.
hasIneqs = (nineqcstr > 0); % Does the problem have any inequalities?
hasEqsAndBnds = (neqcstr > 0) && (any(isfinite(ub)) || any(isfinite(lb))); % Does the problem have both equalities and bounds?
hasMoreEqsThanVars = (neqcstr > numberOfVariables); % Does the problem have more equalities than variables?
hasNoConstrs = (neqcstr == 0) && (nineqcstr == 0) && ...all(eq(ub, inf)) && all(eq(lb, -inf)); % Does the problem not have equalities, bounds, or inequalities?if (hasIneqs || hasEqsAndBnds || hasMoreEqsThanVars || hasNoConstrs) && ...strcmpi(output.algorithm,trustRegReflect) || strcmpi(output.algorithm,activeSet)% (has linear inequalites OR both equalities and bounds OR has no constraints OR% has more equalities than variables) then call active-set codeif algChoiceOptsConflict% Active-set algorithm chosen as a result of conflicting optionswarning('optim:quadprog:QPAlgLargeScaleConflict', ...['Options LargeScale = ''off'' and Algorithm = ''trust-region-reflective'' conflict. ' ...'Ignoring Algorithm and running active-set algorithm. To run trust-region-reflective, set ' ...'LargeScale = ''on''. To run active-set without this warning, set Algorithm = ''active-set''.']);endif strcmpi(output.algorithm,trustRegReflect)warning('optim:quadprog:SwitchToMedScale', ...['Trust-region-reflective algorithm does not solve this type of problem, ' ...'using active-set algorithm. You could also try the interior-point-convex ' ...'algorithm: set the Algorithm option to ''interior-point-convex'' ', ...'and rerun. For more help, see %s in the documentation.'], ...addLink('Choosing the Algorithm','choose_algorithm'))endoutput.algorithm = activeSet;Algorithm = 'active-set';if issparse(H) || issparse(A) || issparse(Aeq) % Passed in sparse matriceswarning(message('optim:quadprog:ConvertingToFull'))endH = full(H); A = full(A); Aeq = full(Aeq);
else% Using trust-region-reflective or interior-point-convex algorithmsif ~usrSuppliedHessMultH = sparse(H);endA = sparse(A); Aeq = sparse(Aeq);
end
if ~isa(H,'double') || usrSuppliedHessMult && ...~strcmpi(output.algorithm,trustRegReflect)error(message('optim:quadprog:NoHessMult', Algorithm))
endif diagnostics % Do diagnostics on information so fargradflag = []; hessflag = []; line_search=[];constflag = 0; gradconstflag = 0; non_eq=0;non_ineq=0;lin_eq=size(Aeq,1); lin_ineq=size(A,1); XOUT=ones(numberOfVariables,1);funfcn{1} = [];ff=[]; GRAD=[];HESS=[];confcn{1}=[];c=[];ceq=[];cGRAD=[];ceqGRAD=[];msg = diagnose('quadprog',output,gradflag,hessflag,constflag,gradconstflag,...line_search,options,defaultopt,XOUT,non_eq,...non_ineq,lin_eq,lin_ineq,lb,ub,funfcn,confcn,ff,GRAD,HESS,c,ceq,cGRAD,ceqGRAD);
end% Trust-region-reflective
if strcmpi(output.algorithm,trustRegReflect)% Call sqpmin when just bounds or just equalities[X,fval,output,exitflag,lambda] = sqpmin(f,H,mtxmpy,X0,Aeq,Beq,lb,ub,verbosity, ...options,defaultopt,computeLambda,computeConstrViolation,varargin{:});if exitflag == -10 % Problem not handled by sqpmin at this time: dependent rowswarning(message('optim:quadprog:SwitchToMedScale'))output.algorithm = activeSet;if ~isa(H,'double') || usrSuppliedHessMulterror('optim:quadprog:NoHessMult', ...'H must be specified explicitly for active-set algorithm: cannot use HessMult option.')endH = full(H); A = full(A); Aeq = full(Aeq);end
end
% Call active-set algorithm
if strcmpi(output.algorithm,activeSet)if isempty(X0)X0 = zeros(numberOfVariables,1); end% Set default value of MaxIter for qpsubdefaultopt.MaxIter = 200;% Create options structure for qpsubqpoptions.MaxIter = optimget(options,'MaxIter',defaultopt,'fast');% A fixed constraint tolerance (eps) is used for constraint% satisfaction; no need to specify any valueqpoptions.TolCon = [];[X,lambdaqp,exitflag,output,~,~,msg]= ...qpsub(H,f,[Aeq;A],[Beq;B],lb,ub,X0,neqcstr,...verbosity,caller,ncstr,numberOfVariables,qpoptions); output.algorithm = activeSet; % have to reset since call to qpsub obliteratesendif strcmpi(output.algorithm,interiorPointConvex)defaultopt.MaxIter = 200;defaultopt.TolFun = 1e-8;% If the output structure is requested, we must reconstruct the% Lagrange multipliers in the postsolve. Therefore, set computeLambda% to true if the output structure is requested.flags.computeLambda = computeFirstOrderOpt; flags.detailedExitMsg = detailedExitMsg;flags.verbosity = verbosity;[X,fval,exitflag,output,lambda] = ipqpcommon(H,f,A,B,Aeq,Beq,lb,ub,X0, ...flags,options,defaultopt,varargin{:});% Presolve may have removed variables and constraints from the problem.% Postsolve will re-insert the primal and dual solutions after the main% algorithm has run. Therefore, constraint violation and first-order% optimality must be re-computed.% % If no initial point was provided by the user and the presolve has% declared the problem infeasible or unbounded, X will be empty. The% lambda structure will also be empty, so do not compute constraint% violation or first-order optimality if lambda is missing.% Compute constraint violation if the output structure is requestedif computeFirstOrderOpt && ~isempty(lambda)output.constrviolation = norm([Aeq*X-Beq; max([A*X - B;X - ub;lb - X],0)],Inf); end
end% Compute fval and first-order optimality if the active-set algorithm was
% run, or if the interior-point-convex algorithm was run (not stopped in presolve)
if (strcmpi(output.algorithm,interiorPointConvex) && ~isempty(lambda)) || ...strcmpi(output.algorithm,activeSet)% Compute objective function valuefval = 0.5*X'*(H*X)+f'*X;% Compute lambda and exit message for active-set algorithmif strcmpi(output.algorithm,activeSet)if computeLambda || computeFirstOrderOptllb = length(lb);lub = length(ub);lambda.lower = zeros(llb,1);lambda.upper = zeros(lub,1);arglb = ~isinf(lb); lenarglb = nnz(arglb);argub = ~isinf(ub); lenargub = nnz(argub);lambda.eqlin = lambdaqp(1:neqcstr,1);lambda.ineqlin = lambdaqp(neqcstr+1:neqcstr+nineqcstr,1);lambda.lower(arglb) = lambdaqp(neqcstr+nineqcstr+1:neqcstr+nineqcstr+lenarglb);lambda.upper(argub) = lambdaqp(neqcstr+nineqcstr+lenarglb+1: ...neqcstr+nineqcstr+lenarglb+lenargub);endif exitflag == 1normalTerminationMsg = sprintf('Optimization terminated.');if verbosity > 0disp(normalTerminationMsg)endif isempty(msg)output.message = normalTerminationMsg;else% append normal termination msg to current output msgoutput.message = sprintf('%s\n%s',msg,normalTerminationMsg);endelseoutput.message = msg;endend% Compute first order optimality if neededif computeFirstOrderOpt && ~isempty(lambda)output.firstorderopt = computeKKTErrorForQPLP(H,f,A,B,Aeq,Beq,lb,ub,lambda,X); elseoutput.firstorderopt = []; endoutput.cgiterations = [];
end结果:绿线为目标轨迹,红虚线为mpc控制车辆运行轨迹