目录
1.前缀和
2.前缀和算法的好处
3.二维前缀和
4.差分
5.一维差分
6.二维差分
1.前缀和
前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和,而差分可以看成前缀和的逆运算。合理的使用前缀和与差分,可以将某些复杂的问题简单化。
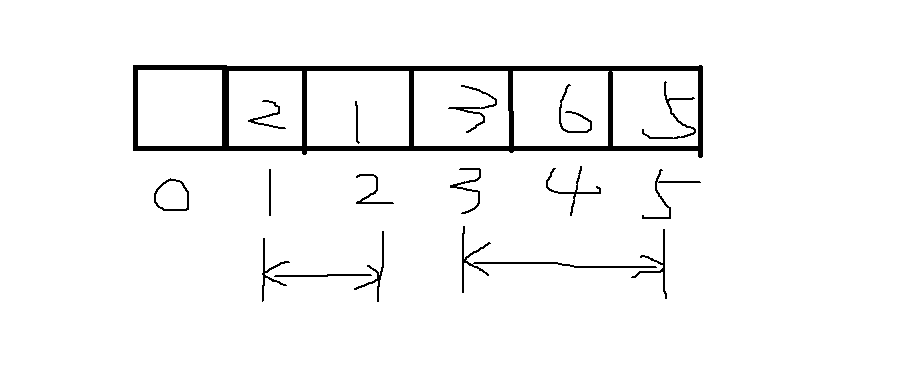
原数组: a[1], a[2], a[3], a[4], a[5], …, a[n]
前缀和 Si为数组的前 i项和
前缀和: S[i] = a[1] + a[2] + a[3] + … + a[i]
注意:前缀和下标一定要从1开始,避免进行下下标的转换。
前缀和的作用:快速求出元素组中某一段区间的和。

2.前缀和算法的好处
假如给出这样一个问题:一个长度为n的整数数组,接下来在输入m个询问,每次询问输入一对l,r,输出原整数数组第l个数到r个数的和。
暴力做法,遍历区间求和。
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
while(m--)
{int l,r;int sum=0;scanf("%d%d",&l,&r);for(int i=l;i<=r;i++){ sum+=a[i];}printf("%d\n",sum);
}时间复杂度为o(n*m),如果n,m数较大的时候就会有时间超限的可能,而我们利用前缀和来求时间复杂度是O(n+m)。
前缀和做法:
首先做一个预处理,定义一个sum[]数组,sum[]来存储前i个数的和。
预处理:
for(int i=1;i<=n;i++)
{ sum[i]=sum[i-1]+a[i];
}询问某一区间的前缀和:
sum[r]-sum[l-1];每次询问只需要执行sum[r]-sum[l-1],时间复杂度为o(1);
我们将这种称为一维前缀和。
一维前缀和总结:
1.for循环求出 每个sum[i] (将 sum[0] 定义为 0, 避免下标的转换)
2.求 [l, r]中的和, 即为 sum[r] - sum[l-1]
例题:
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n个整数,表示整数数列。
接下来 m行,每行包含两个整数 l 和 r,表示一个询问的区间范围。
输出格式
共 m 行,每行输出一个询问的结果。
数据范围
1≤l≤r≤n,
1≤n,m≤100000
−1000≤数列中元素的值≤1000
输入样例:
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例:
3
6
10代码如下:
#include<iostream>
using namespace std;
const int N=100010;
int n,m;
int a[N],s[N];
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];while(m--){int l,r;scanf("%d%d",&l,&r);printf("%d\n",s[r]-s[l-1]);}return 0;
}3.二维前缀和
假设一个问题:输入一个n行m列的整数矩阵,再输入q个询问,每个询问包含四个整数x1, y1, x2, y2,表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。
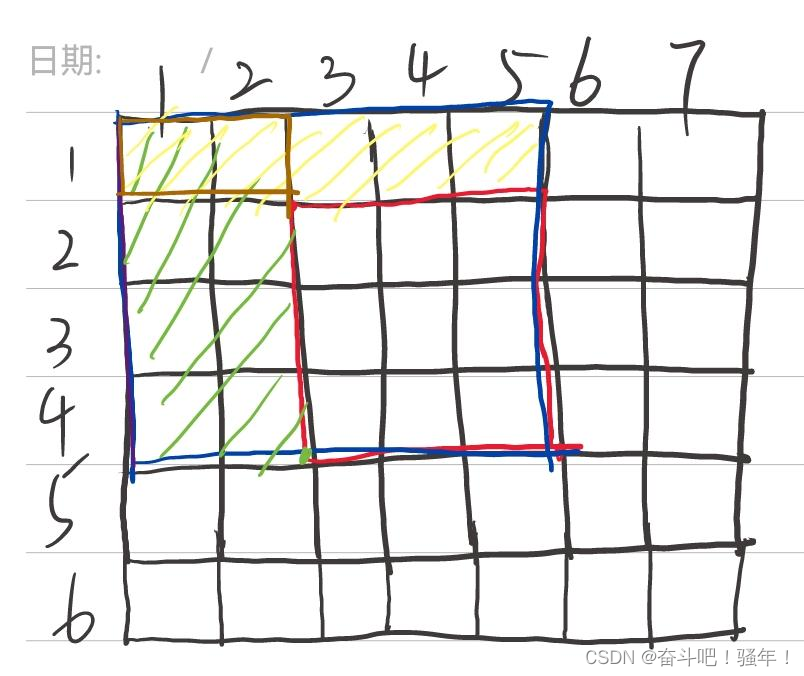
同一维前缀和一样,我们先来定义一个二维数组s[][], s[i][j]表示二维数组中,左上角(1,1)到右下角( i,j )所包围的矩阵元素的和。

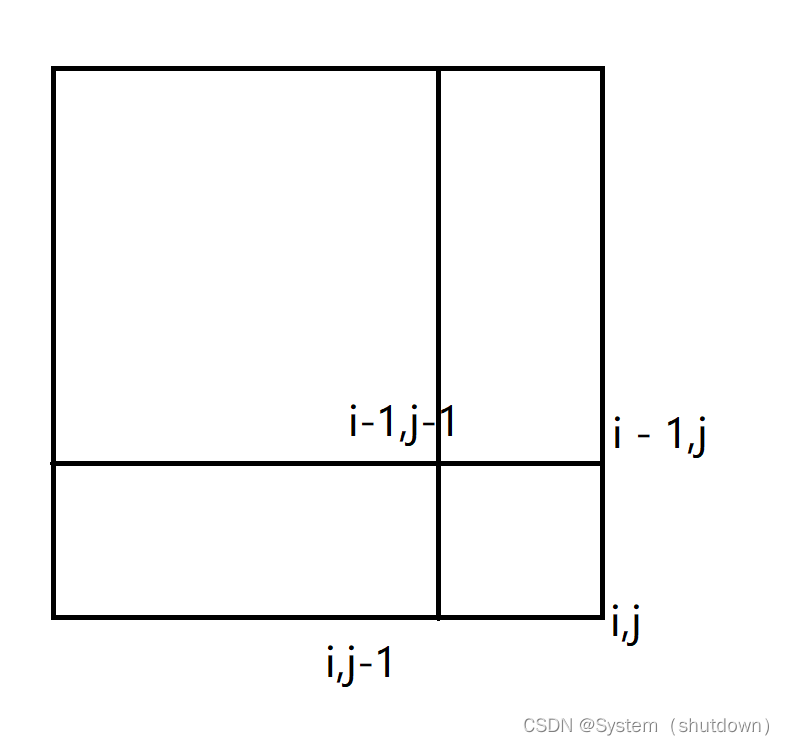
1.s[i][j]为图一的红色部分
s[i][j]=s[i-1][j]+s[i][j-1]+a[i][j]-s[i-1][j-1];
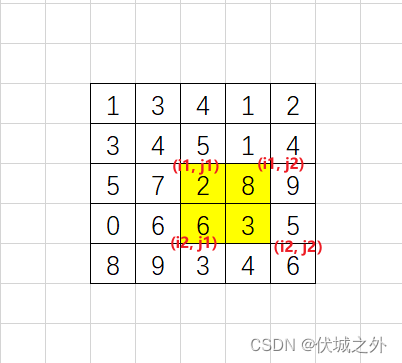
2.(x1,y1)(x2,y2)表示图二的红色部分
s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];
二维前缀和总结:

例题:
输入一个 n行 m 列的整数矩阵,再输入 q个询问,每个询问包含四个整数 x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n,m,q。
接下来 n行,每行包含 m 个整数,表示整数矩阵。
接下来 q行,每行包含四个整数 x1,y1,x2,y2,表示一组询问。
输出格式
共 q行,每行输出一个询问的结果。
数据范围
1≤n,m≤1000
1≤q≤200000
1≤x1≤x2≤n
1≤y1≤y2≤m
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
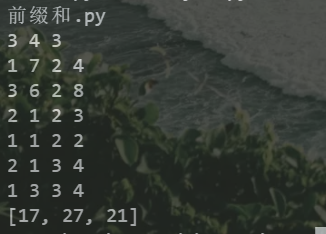
输出样例:
17
27
21
代码如下:
#include<iostream>
using namespace std;
const int N=1010;
int n,m,q;
int a[N][N],s[N][N];
int main()
{scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)s[i][j]=s[i-1][j]+s[i][j-1]+a[i][j]-s[i-1][j-1];while(q--){int x1,y1,x2,y2;scanf("%d%d%d%d",&x1,&y1,&x2,&y2);printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);}return 0;
}4.差分

5.一维差分
差分可以看作是前缀和的逆运算。
差分数组:
首先给定一个原数组a:a[1], a[2], a[3],,,,,, a[n];
然后我们构造一个数组b : b[1] ,b[2] , b[3],,,,,, b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]
也就是说,a数组是b数组的前缀和数组,反过来我们把b数组叫做a数组的差分数组。换句话说,每一个a[i]都是b数组中从头开始的一段区间和。
差分的作用:
可以快速的将某一段区域加上一个数,例如在区间l,r中间加上c;给a数组中的[ l, r]区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c。时间复杂度为O(1), 大大提高了效率。
一维差分总结:给区间[l,r]中的每一个数加上c:b[l] + = c, b[r+1] - = c
例题:
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n和 m。
第二行包含 n个整数,表示整数序列。
接下来 m行,每行包含三个整数 l,r,c,表示一个操作。
输出格式
共一行,包含 n个整数,表示最终序列。
数据范围
1≤n,m≤100000
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2#include<iostream>
using namespace std;
const int N=100010;
int n,m;
int a[N],b[N];
void f(int l,int r,int c)
{b[l]+=c;b[r+1]-=c;
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) f(i,i,a[i]);while(m--){int l,r,c;scanf("%d%d%d",&l,&r,&c);f(l,r,c);}for(int i=1;i<=n;i++) b[i]+=b[i-1];for(int i=1;i<=n;i++) printf("%d ",b[i]);return 0;
}6.二维差分

b[x1][ y1 ] +=c ; 让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1][y2+1]-=c ; 让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y1]- =c ; 让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y2+1]+=c; 让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。
二维差分总结

例题:
输入一个 n 行 m 列的整数矩阵,再输入 q个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1)(x1,y1) 和 (x2,y2)(x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n行,每行包含 m个整数,表示整数矩阵。
接下来 q行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n行,每行 m个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m
−1000≤c≤1000
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2
#include<iostream>
using namespace std;
const int N=1010;
int n,m,q;
int a[N][N],b[N][N];
void f(int x1,int y1,int x2,int y2,int c)
{b[x1][y1]+=c;b[x2+1][y1]-=c;b[x1][y2+1]-=c;b[x2+1][y2+1]+=c;
}
int main()
{cin>>n>>m>>q;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>a[i][j];for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)f(i,j,i,j,a[i][j]);while(q--){int x1,y1,x2,y2,c;cin>>x1>>y1>>x2>>y2;f(x1,y1,x2,y2,c);}for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];for(int i = 1; i <= n; i ++ ){for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);puts("");}return 0;
}