💛 前情提要💛

本章节是每日一算法的二维前缀和算法的相关知识~

接下来我们即将进入一个全新的空间，对代码有一个全新的视角~

以下的内容一定会让你对数据结构与算法有一个颠覆性的认识哦！！！

❗以下内容以C++的方式实现，对于数据结构与算法来说最重要的是思想哦❗

以下内容干货满满，跟上步伐吧~

---

作者介绍：

🎓 作者： 热爱编程不起眼的小人物🐐
🔎作者的Gitee：代码仓库
📌系列文章&专栏推荐： 《刷题特辑》、 《C语言学习专栏》、《数据结构_初阶》 、《C++轻松学_深度剖析_由0至1》、《Linux - 感受系统美学》

📒我和大家一样都是初次踏入这个美妙的“元”宇宙🌏 希望在输出知识的同时，也能与大家共同进步、无限进步🌟
🌐这里为大家推荐一款很好用的刷题网站呀👉点击跳转

---

📌导航小助手📌

• 💡本章重点
• 🍞前缀和
• • 🏷️子矩阵的和【难度：简单】
• 🫓总结

---

💡本章重点

• 二维前缀和的算法理解&应用

---

🍞前缀和

💡二维前缀和算法：

• 本质：就是计算前i个数组元素的和

• 二前缀和对于计算数组中某一段连续区间元素的和有奇效

  • 即我们无需每次计算某一段连续区间的和时都遍历一次数组

  • 我们只需要计算一次数组中每个位置对应的前缀和并把其存储起来，这样我们就能利用相减，去求出某一段区间的前缀和了

👉如何计算二维前缀和：

• 在我们之前已经有一维数组前缀和算法的基础上，我们不妨会想到：

  • 计算二维数组前缀和，不就和计算一维数组前缀和一样，即计算每一个位置的前缀和就相当于：

  • 此位置的前缀和 = 这个位置的值 + 此位置前的前缀和

  • Eg：s[3][1] = a[0][0] + a[0][1] + a[0][2] + a[0][3] +a[1][1] + a[1][2] + …… + a[3][1]

• 但事实真的是这样吗？其实不是的，如果按照上述的方式去计算二维数组前缀和的话，本质其实就相当于遍历了一次二维数组，其时间复杂度就为O(N*M)了，其实已经偏离了前缀和的本心了

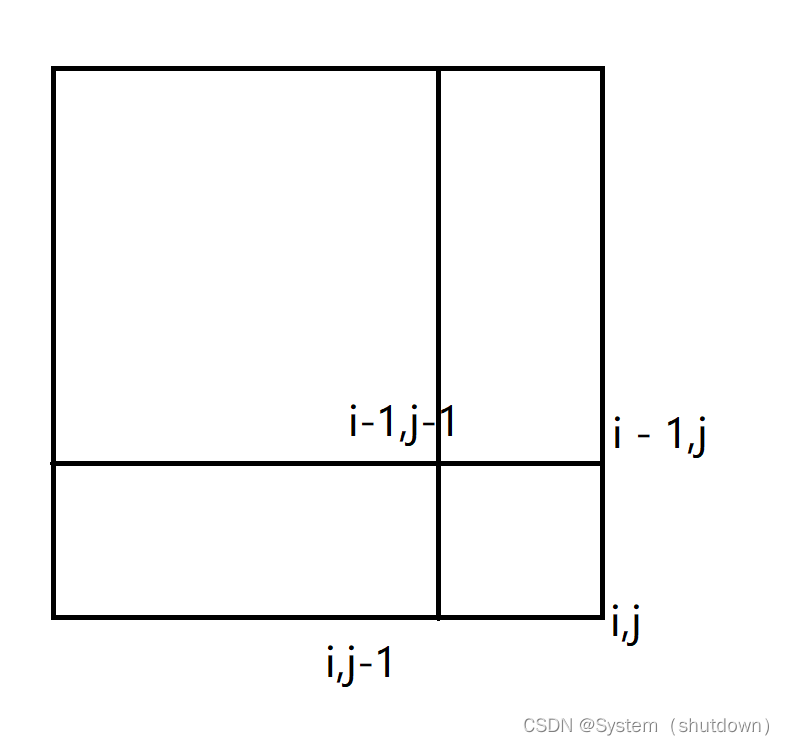
• 所以，在这里我们计算前缀和采取了另外一种计算策略：拼接

  简单来说，就是遵循：计算哪个点的前缀和，就以这个点的横纵左边为边界，计算此点与起点（[1，1]）之间所形成的矩阵内所有元素的和 的原则

👉综上，便可以得出两条重要公式

1️⃣计算某一个位置的前缀和

S[i, j] = 第i行j列格子与起点（[1,1]）所围成的矩阵中所有元素的和

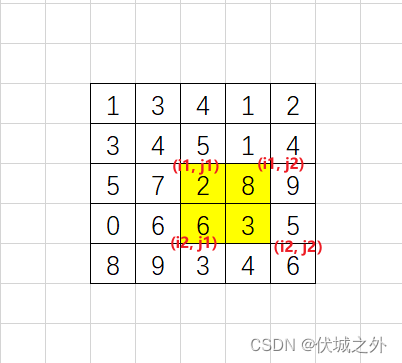
2️⃣计算某一区间的前缀和

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

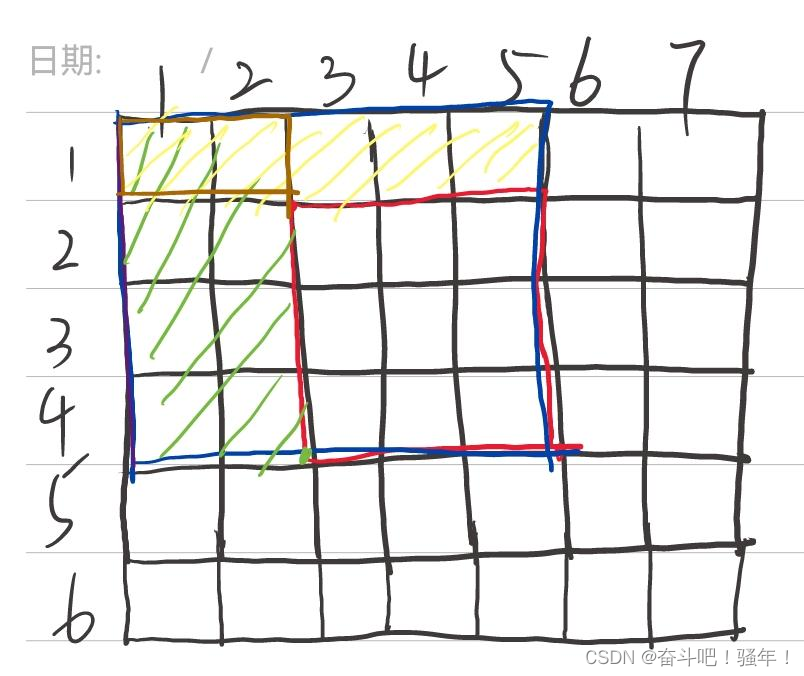
🌰计算二维前缀和动图示例：

1️⃣计算某一个位置的前缀和

• 如上图所示，计算某个点的前缀和，实际就是计算被涂上色块的元素的和

2️⃣计算某一区间的前缀和

• 如上图所示，正是有了这种拼接的计算方式，在计算某一区间的前缀和的时候，便可以利用如上述形象的表达方式，去删减比我们想要得到的区间的前缀和多出的范围

❗特别注意：

• 我们看见原来的二维数组中第一行和第一列都是空出来的，因为我们将其默认初始化为0了

• 这是为了防止边界问题的出现，我们的数据都是从数组下标为1开始存储的

➡️那我们就来道题目试验一下吧~

---

🏷️子矩阵的和【难度：简单】

输入一个 $n$ 行 $m$ 列的整数矩阵，再输入 $q$ 个询问，每个询问包含四个整数 $x1$, $y1$, $x2$, $y2$，表示一个子矩阵的左上角坐标和右下角坐标

对于每个询问输出子矩阵中所有数的和

输入格式

第一行包含三个整数 $n$，$m$，$q$

接下来 $n$ 行，每行包含 $m$ 个整数，表示整数矩阵

接下来 $q$ 行，每行包含四个整数 $x1$, $y1$, $x2$, $y2$，表示一组询问

输出格式

共 $q$ 行，每行输出一个询问的结果

数据范围

$1\le n,m\le 1000$ ,

$1\le q\le 200000,$

$1\le x1\le x2\le n$,

$1\le y1\le y2\le m$,

$-1000\le 矩阵内元素的值\le 1000$

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
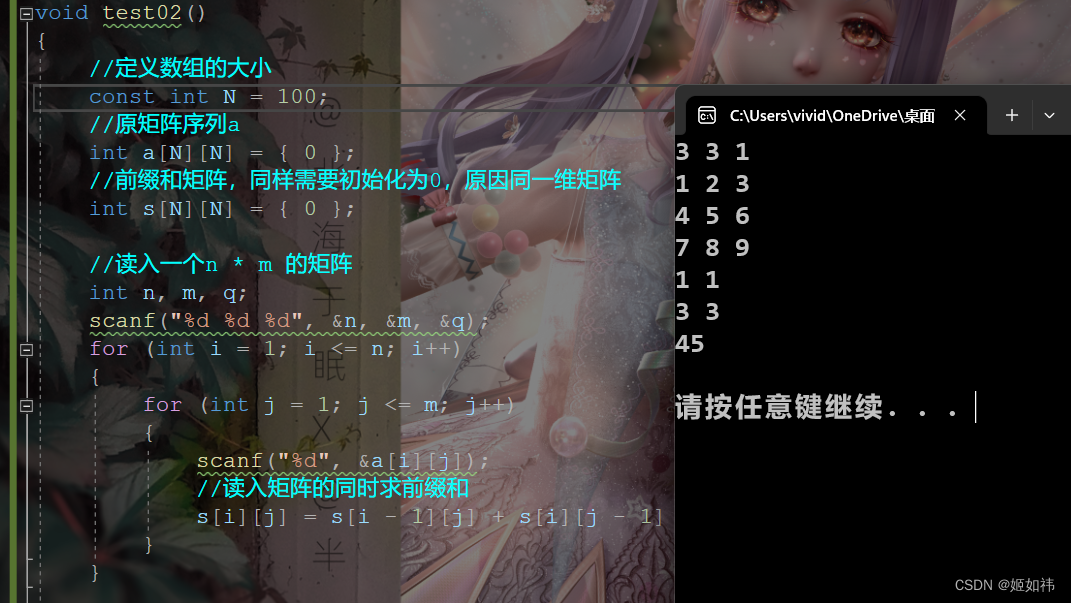
21

👉代码实现：

#include <iostream>using namespace std;const int N = 1010;int a[N][N],s[N][N];int n, m, q;int main()
{cin>>n>>m>>q;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){scanf("%d",&a[i][j]);}}for(int i = 0; i <= n; i++){for(int j = 1; j <= m; j++){s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];}}while(q --){int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] << endl;}return 0;
}

---

🫓总结

综上，我们基本了解了算法基础中的 “二维前缀和算法” 🍭 的知识啦~~

恭喜你的内功又双叒叕得到了提高！！！

感谢你们的阅读😆

后续还会继续更新💓，欢迎持续关注📌哟~

💫如果有错误❌，欢迎指正呀💫

✨如果觉得收获满满，可以点点赞👍支持一下哟~✨