前缀和与及经典例题详解

南昌理工ACM集训队

前言

下面的例题都出自于洛谷官方算法2-1题单，有兴趣的同学可以去水一水，题目很简单孩子已经吃了两箱了
题单传送门

本人小白如有不对欢迎指正ლ(╹◡╹ლ)

前缀和

前缀和，顾名思义就是从第一个数到第i个数之间所有数的总和。一般用在对数组的预处理，在解决某问题时如果需要多次用到数组区间内的和，用前缀和预处理目标数组会是个不错的选择。

那么前缀和怎么获得呢

前缀和是从第一个数到第i个数之间的总和，所以我们可以利用动态规划的思想，输入数组第i个数的时候只要在输入之后加上i-1的前缀和就可以得到当前第i个数的前缀和。
如下

//设前缀和数组为a[N]
for (int i = 1; i <= N; i++) {cin >> a[i];a[i] = a[i - 1] + a[i];}

那么区间[ l , r ]之间的和怎么获得呢

我们知道前缀和数组中的第 i 个数是原数组从第1个到第 i 个数的总和，所以设前缀和数组为a,原数组为ori

a[ l ] = ori[ 1 ]+ori[ 2 ]+ori[ 3 ]+…+ori[ l-1 ]+ori[ l ]
a[ r ] = ori[ 1 ]+ori[ 2 ]+ori[ 3 ]+…+ori[ r-1 ]+ori[ r ]

所以用a[ r ]减去a[ l-1 ]即得 ori[ l ]+ori[ l+1 ]+…+ori[ r-1 ]+ori[ r ]，即区间[ l , r ]之间的总和。
即

a[i] = a[i - 1] + a[i];

知道了前缀和及其原理后，就可以用来水题了ヽ(°◇° )ノ

P5638 光骓者的荣耀

传送门
一道非常经典的模板题
小k需要得到最快从第 1 个城市走到第 i 个城市并且遍历所有城市的时间，相邻两个城市有不同长度的路连接，他有一个可以从第 i 个城市传送到第 i+k 个城市的不花时间的传送门。
不难推断按顺序从第 1 个城市走到最后一个城市是最快的，求出所有路线的总和再用总和减去传送门能传送的最大距离就是最后的答案。
那么求出传送门能传送的最大距离就是这道题的关键，很容易就能想到前缀和的思想，先预处理一个前缀和数组，用第 k 个数减去第 i-1 个数就能得到从第 i 个城市到第 k 个城市的路线总和
遍历一下所有的传送门传送距离就能得出最大的传送门能传送的距离

代码如下

#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
ll a[1000010];
int main()
{ll n, k, s = 0;scanf("%lld%lld", &n, &k);for (int i = 1; i < n; i++) {scanf("%lld", &a[i]);a[i] = a[i - 1] + a[i];if (i < k) {//如果i小于k则传送门只能传送第一个城市到第k个城市的距离s = max(s, a[i] - a[0]);}else {s = max(s, a[i] - a[i - k]);}}printf("%lld", a[n - 1] - s);//s为最大传送门距离
}

二维前缀和

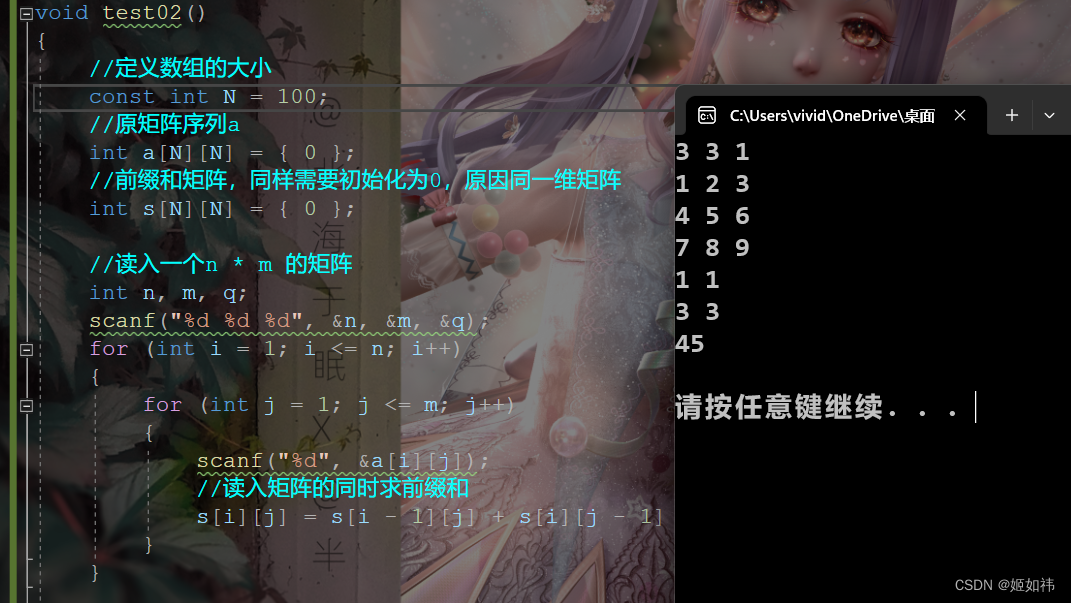
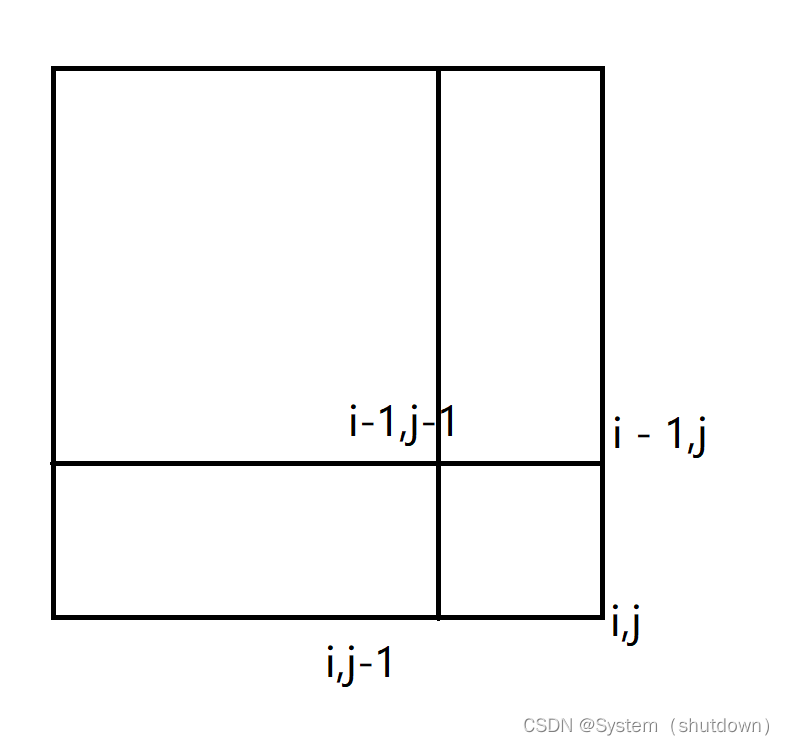
二维前缀和，顾名思义就是一维前缀和的二维形态，设原二维数组为 ori[ i ][ j ] ，二维前缀和数组为 a[ i ][ j ]，如图所示

蓝色的部分和红色的部分相加，再减去两部分重叠的绿色部分，最后加上右上角的ori[ i ][ j ]，即为要求的黑色部分 a[ i ][ j ]
因此求二维前缀和的公式为

a[ i ][ j ] = a[ i ][ j-1 ] + a[ i-1 ][ j ] - a[ i-1][ j-1 ] + ori[ i ][ j ]

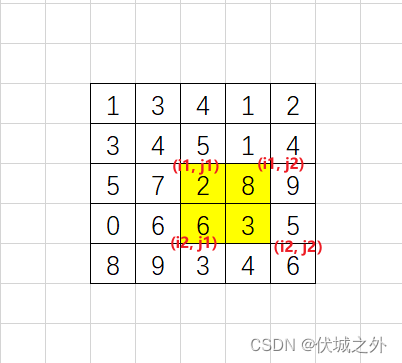
同理，求矩阵x1，y1到x2，y2之间的矩阵和的公式为

s = a[ x2 ][ y2 ] - a[ x1-1 ][ y2 ] - a[ x2 ][ y1-1 ] + ori[ x1-1 ][ y1-1 ]

接下来上一道非常简单的例题

P2004 领地选择

传送门

题意很简单，求地图上边长为c的价值总和最大的正方形土地。只要我们遍历一遍地图，将地图上每个点的二维前缀和算出，再利用二维前缀和算出所有边长为c的正方形土地的价值总和，比较大小即可快速求出答案

#include<iostream>
#include<algorithm>
using namespace std;int a[1010][1010];
int main()
{int n, m, c, ma, ansx = 0, ansy = 0;scanf("%d%d%d", &n, &m, &c);for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {scanf("%d", &a[i][j]);a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + a[i][j];//二维前缀和预处理}}ma = a[0 + c][0 + c] - a[0][0 + c] - a[0 + c][0] + a[0][0];//初始为第一个边长为c的正方形矩阵for (int i = c; i <=n; i++) {for (int j = c; j <=n; j++) {if (ma < a[i][j] - a[i - c][j] - a[i][j - c] + a[i - c][j - c]) {ansx = i, ansy = j;//记录最大值的坐标}ma = max(ma, a[i][j] - a[i - c][j] - a[i][j - c] + a[i - c][j - c]);}}cout << ansx -c+1 << " " << ansy -c+1;//输出结果
}

最大子段和

前缀和在解题中有非常广泛的应用，其中一种就是求一个数组的最大连续子数组，利用前缀和的原理遍历一遍数组即可求出，时间复杂度为O(n)

P1115 最大子段和

传送门

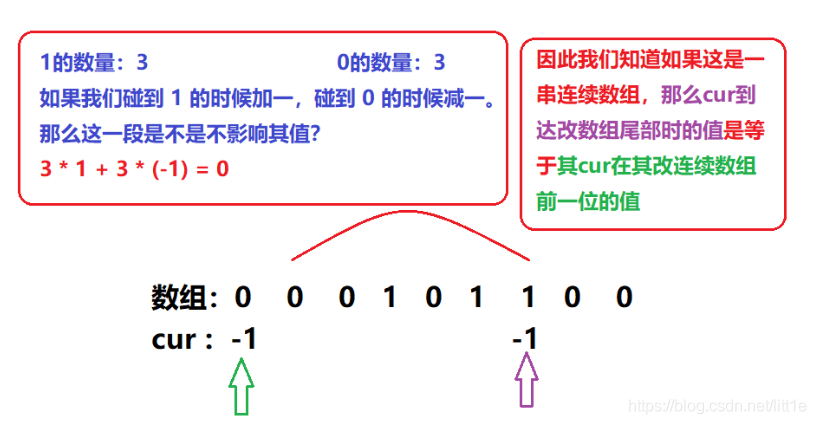
在求最大子段的类似的题中，我们利用的是类似前缀和的动态规划思想

设原数组为a[N]，动态规划数组为dp[N]
第一个数为一个有效序列。
如果一个数加上上一个有效序列得到的结果比这个数大，那么该数也属于这个有效序列。
如果一个数加上上一个有效序列得到的结果比这个数小，那么这个数单独成为一个新的有效序列。
最后处理所有有效序列，输出最大的即可

状态方程为

dp[i]=max(dp[i],dp[i-1]+a[i])

附ac代码

#include<iostream>
using namespace std;
int a[200010];
int main()
{int n, ans = -10000;cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];a[i] = max(a[i], a[i - 1] + a[i]);ans = max(ans, a[i]);}cout << ans;
}

P1719 最大加权矩形

传送门

与上面一维的求最大子串一样，求二维最大加权矩形的原理大同小异。只要我们利用降维的思想将二维矩阵降为一维的数组，就可以利用上面的公式求出最大的子串，进而求出最大的子矩阵和。

我们用两层循环，遍历子矩阵的上区间和下区间，然后再用一层循环遍历区间之内的每一列的和，然后求出最大的连续的列的和，即可得到最后的答案。输入时利用前缀和的方法预处理每一列的矩阵，方便之后计算每一列的和。

状态方程与上面一维的相同

dp[i]=max(dp[i],dp[i-1]+a[i])

	for (int i = 1; i <= n; i++) {for (int j = i; j <= n; j++) {int x = 0;for (int k = 1; k <= n; k++) {x=max(a[j][k] - a[i - 1][k],a[j][k] - a[i - 1][k]+x);ans = max(ans, x);}}}

暴力计算的时间复杂度为 O( n ^ 4 )，而利用dp与前缀和的思想解决这道题时间复杂度只有O( n ^ 3 )，大大缩短了时间，提高了代码效率。

最后快码加编

#include<iostream>
using namespace std;
int a[200][200];
int main()
{int n, ans = -128;cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {scanf("%d", &a[i][j]);a[i][j] = a[i - 1][j] + a[i][j];//预处理每一列的前缀和}}for (int i = 1; i <= n; i++) {//遍历下区间for (int j = i; j <= n; j++) {//遍历上区间int x = 0;for (int k = 1; k <= n; k++) {x=max(a[j][k] - a[i - 1][k],a[j][k] - a[i - 1][k]+x);//遍历区间内每一列的最大连续子串和ans = max(ans, x);}}}cout << ans << endl;//轻松ac
}

写在最后

前缀和的思想在很多的题目里都能用到，前缀和主要用于预处理各种数组，以达到快速计算数组的某一区间的和的目的，大量优化代码运行时间，以后碰到类似的求子串和、最大子串的题目时，不妨思考利用前缀和，结合贪心、dp的思想，解决求区间最大、最小值的问题

谢谢你看到最后ლ(╹◡╹ლ)