二维前缀和

直接看一个例子
假设给定一个矩阵
1 2 4 3
5 1 2 4
6 3 5 9

那么，可以推出他的二维前缀和矩阵为
1 3 7 10
6 9 15 22
12 18 29 45
在二维前缀和数组中，9 = 1 + 2 + 5 + 1
15 = 1 + 2 + 5 + 1 + 4 + 2
18 = 1+ 5 + 6 + 2 + 1 + 3… …
即二位前缀和数组中第 i 行第 j 列的数值等于原数组中第 i 行第 j 列之前（即左上角）所有数的和

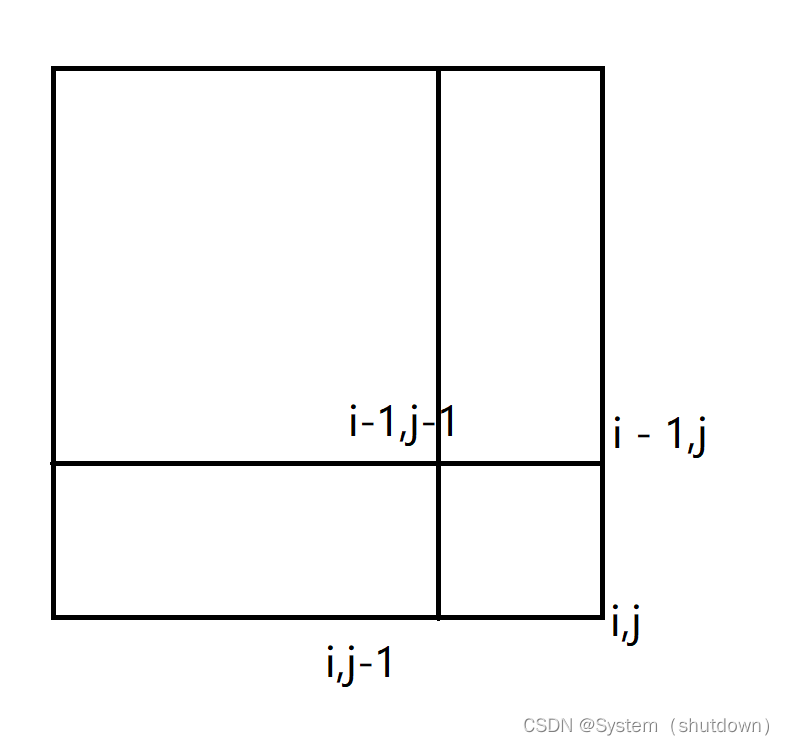
下图中，以x表示行，y表示列

图中我们标注出四个点。

坐标(x，y)左上角所有元素的和，用sum[x][y]表示；
坐标(x，y - 1)左上角所有元素的和，用sum[x][y-1]表示；
坐标(x - 1，y)左上角所有元素的和，用sum[x-1][y]表示；
坐标(x - 1，y - 1)左上角所有元素的和，用sum[x-1][y-1]表示。

假设第x行第y列对应的数组为 a[x][y] ,二位前缀和为 sum[x][y] ,由容斥原理，得

sum[x][y] = sum[x-1][y] + sum[x][y-1] - sum[x-1][y-1] + a[x][y];

例题

原题链接

题目描述
求一个 n*m 大小的二维矩阵对应的前缀和。
输入
第一行 2 个正整数：N 和 M，N 和 M 范围在[1, 1000]。
其后 N 行，每行 M 个正整数：范围在[1, 10000]。
输出
对应二维数组的前缀和。
样例输入
3 4
1 2 4 3
5 1 2 4
6 3 5 9
样例输出
1 3 7 10
6 9 15 22
12 18 29 45

样例通过可惜代码超时了，有大佬能给出过题代码万分感谢

#include <iostream>
#include <cstdio>using namespace std;const int N = 1010;
long long prefixSum[N][N];//前缀和数组
int nums[N][N];//原数组int main()
{int n,m;scanf("%d%d",&n,&m);for (int i = 1;i <= n;i++)for (int j = 1;j <= m;j++){scanf("%d",&nums[i][j]);//二维前缀和prefixSum[i][j] = prefixSum[i - 1][j] + prefixSum[i][j - 1] - prefixSum[i - 1][j - 1] + nums[i][j];}//输出for (int i = 1;i <= n;i++){for (int j = 1;j <= m;j++){printf("%d ",prefixSum[i][j]);}puts("");}        return 0;
}

二维前缀和的应用
输入一个n行m列的整数矩阵，再输出q个询问，每个询问包含四个整数x1，x2，y1，y2，表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和

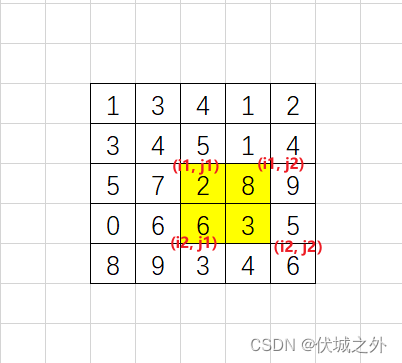
已知(x1,y1)、(x2,y2)，如何求出下图中黄色部分的面积？
设黄色部分面积为ans，设sum[x][y]表示坐标(x,y)左上角所有元素之和则

ans =  sum[x2][y2] - sum[x2][y1-1] - sum[x1-1][y2] + sum[x1-1][y1-1];

例题

原题链接

题目描述
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1，y1，x2，y2，表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入
第一行包含三个整数 n，m，q。
接下来 n 行，每行包含 m 个整数，表示整数矩阵。
接下来 q 行，每行包含四个整数 x1，y1，x2，y2，表示一组询问。
输出
共 q 行，每行输出一个询问的结果。
样例输入
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
样例输出
17
27
21
提示
【数据范围】
1 ≤ n, m ≤ 1000,
1 ≤ q ≤ 200000,
1 ≤ x1 ≤ x2 ≤ n,
1 ≤ y1 ≤ y2 ≤ m,
−1000 ≤ 矩阵内元素的值 ≤ 1000

#include <cstdio>
#include <iostream>using namespace std;const int N = 1010;
int nums[N][N];//原数组
int prefixSum[N][N];//前缀和数组int main()
{int n,m,q;scanf("%d%d%d",&n,&m,&q);//读入数据for (int i = 1;i <= n;i++)for (int j = 1;j <= m;j++){scanf("%d",&nums[i][j]);//计算前缀和数组prefixSum[i][j] = prefixSum[i - 1][j] + prefixSum[i][j - 1] - prefixSum[i - 1][j - 1] + nums[i][j];}//q次循环for (int i = 0;i < q;i++){int x1,x2,y1,y2;scanf("%d%d%d%d",&x1,&y1,&x2,&y2);int ans = prefixSum[x2][y2] - prefixSum[x2][y1 - 1] - prefixSum[x1 - 1][y2] + prefixSum[x1 - 1][y1 - 1];printf("%d\n",ans);}return 0;
}