1、前缀和

前缀和是指某序列的前n项和，可以把它理解为数学上的数列的前n项和，而差分可以看成前缀和的逆运算。合理的使用前缀和与差分，可以将某些复杂的问题简单化。

2、前缀和算法有什么好处？

先来了解这样一个问题：

输入一个长度为n的整数序列。接下来再输入m个询问，每个询问输入一对l, r。对于每个询问，输出原序列中从第l个数到第r个数的和。

我们很容易想出暴力解法，遍历区间求和。

代码如下：

const int N = 1e5 + 10;
int a[N];
int n,m;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
while(m--)
{int l, r;int sum = 0;scanf("%d%d", &l, &r);for(int i = l; i <= r; i++){ sum += a[i];}printf("%d\n",sum);
}

这样的时间复杂度为O(n * m)，如果n和m的数据量稍微大一点就有可能超时，而我们如果使用前缀和的方法来做的话就能够将时间复杂度降到O(n + m)，大大提高了运算效率。

具体做法：

首先做一个预处理，定义一个sum[]数组，sum[i]代表a数组中前i个数的和。

求前缀和运算：

const int N = 1e5 + 10;
int sum[N], a[N]; //sum[i]=a[1]+a[2]+a[3].....a[i];
for(int i = 1;i <= n; i++)
{ sum[i] = sum[i - 1] + a[i];   
}

然后查询操作：

 scanf("%d%d",&l,&r);printf("%d\n", sum[r] - sum[l - 1]);

对于每次查询，只需执行sum[r] - sum[l - 1] ，时间复杂度为O(1)

原理

sum[r] = a[1] + a[2] + a[3] + a[l-1] + a[l] + a[l + 1] ...... a[r];
sum[l - 1] = a[1] + a[2] + a[3] + a[l - 1];
sum[r] - sum[l - 1] = a[l] + a[l + 1] + ......+ a[r];

图解

这样，对于每个询问，只需要执行 sum[r] - sum[l - 1]。输出原序列中从第l个数到第r个数的和的时间复杂度变成了O(1)。

我们把它叫做一维前缀和。

总结：

练习一道题目
输入一个长度为n的整数序列。
接下来再输入m个询问，每个询问输入一对l, r。
对于每个询问，输出原序列中从第l个数到第r个数的和。
输入格式
第一行包含两个整数n和m。
第二行包含n个整数，表示整数数列。
接下来m行，每行包含两个整数l和r，表示一个询问的区间范围。
输出格式
共m行，每行输出一个询问的结果。
数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例：

5 3
2 1 3 6 4
1 2
1 3
2 4

输出样例：

3
6
10

代码：

#include <iostream>using namespace std;const int N = 100010;int n, m;
int a[N], s[N];int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i]; // 前缀和的初始化while (m -- ){int l, r;scanf("%d%d", &l, &r);printf("%d\n", s[r] - s[l - 1]); // 区间和的计算}return 0;
}

3、二维前缀和

如果数组变成了二维数组怎么办呢？

先给出问题：

输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。

同一维前缀和一样，我们先来定义一个二维数组s[][] , s[i][j] 表示二维数组中，左上角(1, 1)到右下角(i, j)所包围的矩阵元素的和。接下来推导二维前缀和的公式。

先看一张图：

紫色面积是指(1, 1)左上角到(i, j - 1)右下角的矩形面积, 绿色面积是指(1, 1)左上角到(i - 1, j )右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。

从图中我们很容易看出，整个外围蓝色矩形面积s[i][j] = 绿色面积s[i - 1][j] + 紫色面积s[i][j - 1] - 重复加的红色的面积s[i - 1][j - 1] + 小方块的面积a[i][j];

因此得出二维前缀和预处理公式

s[i][j] = s[i - 1][j] + s[i][j - 1 ] + a[i] [j] - s[i - 1][j - 1]

接下来回归问题去求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和。

如图：

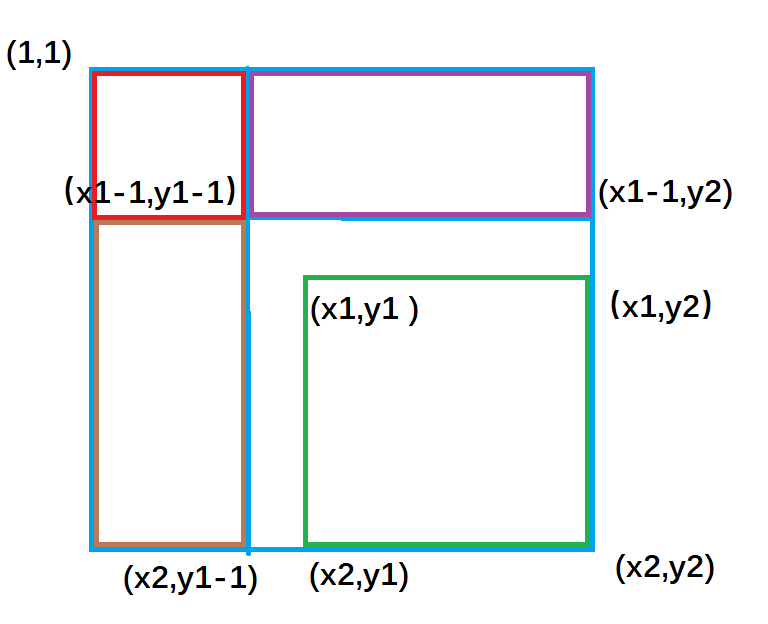
紫色面积是指 (1, 1)左上角到(x1 - 1, y2)右下角的矩形面积 ，黄色面积是指(1, 1)左上角到(x2, y1 - 1)右下角的矩形面积；

不难推出：

绿色矩形的面积 = 整个外围面积s[x2, y2] - 黄色面积s[x2, y1 - 1] - 紫色面积s[x1 - 1, y2] + 重复减去的红色面积 s[x1 - 1, y1 - 1]

因此二维前缀和的结论为：

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]

总结：

练习一道完整题目：
输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数n，m，q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。

输出格式

共q行，每行输出一个询问的结果。

数据范围

1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

代码：

#include <iostream>
using namespace std;
const int N = 1010;
int n, m, q;
int s[N][N];
int main()
{scanf("%d%d%d", &n, &m, &q);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )scanf("%d", &s[i][j]);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];while (q -- ){int x1, y1, x2, y2;scanf("%d%d%d%d", &x1, &y1, &x2, &y2);printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);}return 0;
}

4、差分

---

5、一维差分

类似于数学中的求导和积分，差分可以看成前缀和的逆运算。

差分数组：

首先给定一个原数组a：a[1], a[2], a[3],,,,,, a[n];

然后我们构造一个数组b ： b[1], b[2], b[3],,,,,, b[i];

使得 a[i] = b[1] + b[2] + b[3] + ,,,,,, + b[i]

也就是说，a数组是b数组的前缀和数组，反过来我们把b数组叫做a数组的差分数组。换句话说，每一个a[i]都是b数组中从头开始的一段区间和。

考虑如何构造差分b数组？

最为直接的方法

如下：

a[0 ]= 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

b[3] = a [3] - a[2];

........

b[n] = a[n] - a[n - 1];

图示:

我们只要有b数组，通过前缀和运算，就可以在O(n) 的时间内得到 a 数组 。

知道了差分数组有什么用呢？ 别着急，慢慢往下看。

话说有这么一个问题：

给定区间[l, r ]，让我们把a数组中的[l, r] 区间中的每一个数都加上c,即 a[l] + c , a[l + 1] + c , a[l + 2] + c ,,,,,, a[r] + c;

暴力做法是for循环l到r区间，时间复杂度O(n)，如果我们需要对原数组执行m次这样的操作，时间复杂度就会变成O(n * m)。有没有更高效的做法吗? 考虑差分做法，(差分数组派上用场了)。

始终要记得，a数组是b数组的前缀和数组，比如对b数组的b[i]的修改，会影响到a数组中从a[i]及往后的每一个数。

首先让差分b数组中的 b[l] + c ,通过前缀和运算，a数组变成 a[l] + c ,a[l + 1] + c,,,,,, a[n] + c;

然后我们打个补丁，b[r + 1] - c, 通过前缀和运算，a数组变成 a[r + 1] - c,a[r + 2] - c,,,,,,,a[n] - c;

为啥还要打个补丁？

我们画个图理解一下这个公式的由来:

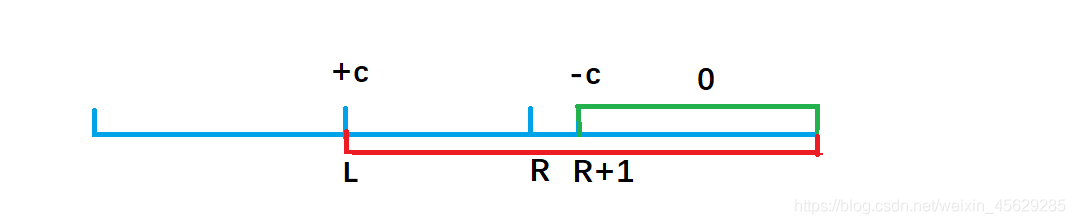
b[l] + c，效果使得a数组中 a[l] 及以后的数都加上了c(红色部分)，但我们只要求l到r 区间加上 c, 因此还需要执行 b[r + 1] - c,让a数组中 a[r + 1]及往后的区间再减去c(绿色部分)，这样对于a[r] 以后区间的数相当于没有发生改变。

因此我们得出一维差分结论：给a数组中的[ l, r] 区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c 。时间复杂度为O(1), 大大提高了效率。

总结：

题目练习： AcWing 797. 差分

输入一个长度为n的整数序列。
接下来输入m个操作，每个操作包含三个整数l, r, c，表示将序列中[l, r]之间的每个数加上c。
请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数n和m。
第二行包含n个整数，表示整数序列。
接下来m行，每行包含三个整数l，r，c，表示一个操作。
输出格式
共一行，包含n个整数，表示最终序列。
数据范围

1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000

输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

AC代码

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N],b[N]; 
int main()
{int n,m;scanf("%d%d", &n, &m);for(int i = 1;i <= n; i++) {scanf("%d", &a[i]);b[i] = a[i] - a[i - 1];      //构建差分数组}int l, r, c;while(m--){scanf("%d%d%d", &l, &r, &c);b[l] += c;     //表示将序列中[l, r]之间的每个数加上cb[r + 1] -= c;}for(int i = 1;i <= n; i++) {b[i] += b[i - 1];  //求前缀和运算printf("%d ",b[i]);}return 0;
}

6、二维差分

如果扩展到二维，我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的，考虑二维差分。

a[][]数组是b[][]数组的前缀和数组，那么b[][]是a[][]的差分数组

原数组： a[i][j]

我们去构造差分数组： b[i][j]

使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。

如何构造b数组呢？

其实关于差分数组，我们并不用考虑其构造方法，因为我们使用差分操作在对原数组进行修改的过程中，实际上就可以构造出差分数组。

同一维差分，我们构造二维差分数组目的是为了 让原二维数组a中所选中子矩阵中的每一个元素加上c的操作，可以由O(n*n)的时间复杂度优化成O(1)

已知原数组a中被选中的子矩阵为 以(x1,y1)为左上角，以(x2,y2)为右下角所围成的矩形区域;

始终要记得，a数组是b数组的前缀和数组，比如对b数组的b[i][j]的修改，会影响到a数组中从a[i][j]及往后的每一个数。

假定我们已经构造好了b数组，类比一维差分，我们执行以下操作
来使被选中的子矩阵中的每个元素的值加上c

b[x1][y1] + = c ;

b[x1,][y2+1] - = c;

b[x2+1][y1] - = c;

b[x2+1][y2+1] + = c;

每次对b数组执行以上操作，等价于：

for(int i = x1;i <= x2;i++)for(int j = y1;j <= y2;j++)a[i][j] += c;

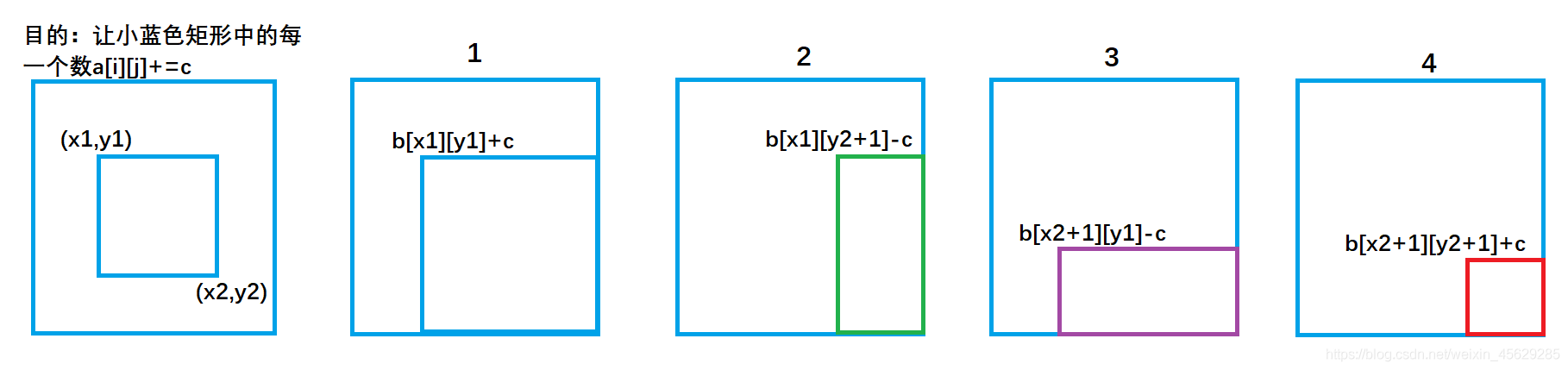
我们画个图去理解一下这个过程：

b[x1][y1] += c ; 对应图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1,][y2 + 1] -= c ; 对应图2 ,让整个a数组中绿色矩形面积的元素再减去c，使其内元素不发生改变。
b[x2 + 1][y1] -= c ; 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c，使其内元素不发生改变。
b[x2 + 1][y2 + 1] += c; 对应图4,让整个a数组中红色矩形面积的元素再加上c，红色内的相当于被减了两次，再加上一次c，才能使其恢复。

我们将上述操作封装成一个插入函数:

void insert(int x1,int y1,int x2,int y2,int c)
{     //对b数组执行插入操作，等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了cb[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}

我们可以先假想a数组为空，那么b数组一开始也为空，但是实际上a数组并不为空，因此我们每次让以(i,j)为左上角到以(i,j)为右下角面积内元素(其实就是一个小方格的面积)去插入 c = a[i][j] ，等价于原数组a中(i,j) 到(i,j)范围内 加上了 a[i][j] ,因此执行 n*m次插入操作，就成功构建了差分b数组.

这叫做曲线救国。

代码如下：

  for(int i = 1;i <= n;i++){for(int j = 1;j <= m;j++){insert(i, j, i, j, a[i][j]);    //构建差分数组}}

当然关于二维差分操作也有直接的构造方法，公式如下：

b[i][j] = a[i][j] − a[i − 1][j] − a[i][j − 1] + a[i −1 ][j − 1]

二维差分数组的构造同一维差分思维相同，因次在这里就不再展开叙述了。

总结：

题目练习： AcWing 798. 差分矩阵
输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数n, m, q。
接下来n行，每行包含m个整数，表示整数矩阵。
接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。
输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。
数据范围

1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

AC代码：

#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}
int main()
{int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j];for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){insert(i, j, i, j, a[i][j]);      //构建差分数组}}while (q--){int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];  //二维前缀和}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){printf("%d ", b[i][j]);}printf("\n");}return 0;
}

如果我的文章对你有帮助，请点点关注，你的关注是对我创作的最大支持。

---