说明:
在进行采购入库的过程中,有必要对表格中的一行进行快速编辑保存,节省时间,提高工作效率!,而不是每次编辑都要弹窗才可编辑
源码:https://gitee.com/charlinchenlin/store-pos
效果图:
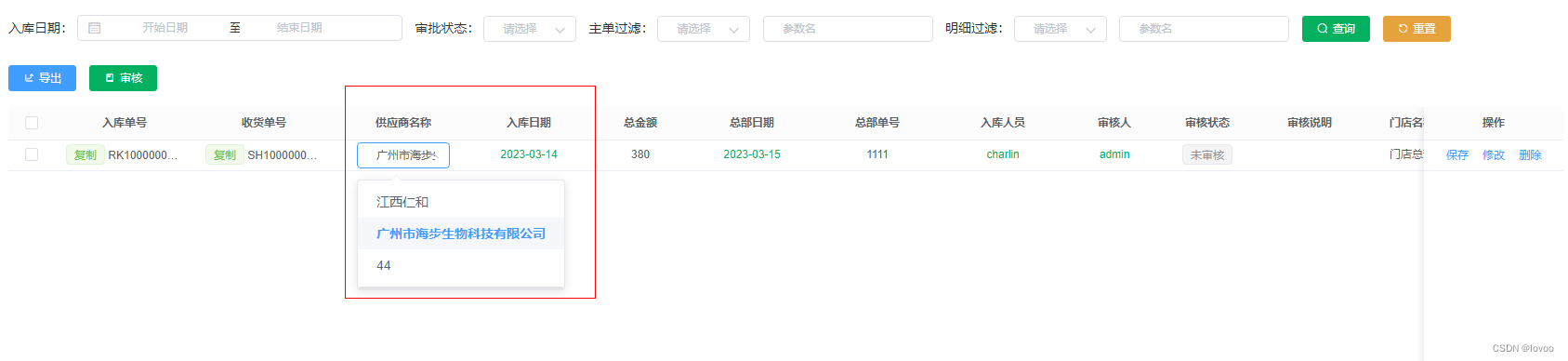
1、在data定义supplier数组等元素
data() {return { suppliers:[], //保存供应商数据 showInput: "", //用来判断是否显示哪个单元格oldData: {}, //用来存修改前的数据currentData: {}, //用来保存新的数据 }},
2、为el-table表格单击和双击添加tableDbEdit事件
<el-table :data="dataList" size="mini" v-loading="dataListLoading" @selection-change="selectionChangeHandle"style="width: 100%;" @cell-click="tableDbEdit" @cell-dblclick="tableDbEdit" height="320":header-cell-style="{ background: '#fcfcfc', color: '#606266', height:'36px'}"><el-table-column type="selection" header-align="center" align="center" width="50"></el-table-column>------</el-table>
控制是否显示select下拉框
tableDbEdit(row, column, event) {this.showInput = column.property + row.inboundId;this.oldData[column.property] = row[column.property];},
3、为供应商列添加下拉框
如果showInput的值与当前的inboundId相同,则显示下拉选项,否则显示数据信息
<el-table-column prop="supplierName" header-align="center" align="center" label="供应商名称" width="150" show-overflow-tooltip><template slot-scope="scope"><el-select size="mini" @focus="getSuppliers()" @click="getSuppliers()" @change='blurInput(scope.row, "supplierName", scope.row.supplierName)' v-model="scope.row.supplierName" clearablev-if="showInput == `supplierName${scope.row.inboundId}`"placeholder="请选择"><el-option v-for="item in suppliers" :key="item.supplierId" :label="item.supplierName" :value="item.supplierName"></el-option></el-select><span v-else class="active-input">{{scope.row.supplierName}}</span></template>
</el-table-column>
聚焦或单击时获取供应商数据
async getSuppliers() {const res = await this.$http({url: `/product/supplier/getSupplies`,method: 'get',params: this.$http.adornParams()})let data = res.dataif (data && data.code === 0) {this.suppliers = data.data}},
触发change事件时给当前列赋值,并设置供应商信息
// 当input失去光标后进行的操作async blurInput(row, name, value) {// 判断数据是否有所改变,如果数据有改变则调用修改接口if (this.oldData[name] != value) {row[name] = value }this.showInput = ""this.currentData = rowif(name === 'supplierName'){this.setSuppliers(row)}},setSuppliers(row) {for (let index in this.suppliers) {let item = this.suppliers[index]if (row.supplierName === item.supplierName) {row.supplierId = item.supplierIdreturn}}},
4、保存当前列,成功后重新加载数据
async saveHandle(row) {console.log("saveHandle row===", row)row.status = row.status ? 1 : 0const res = await this.$http({url: `/purchase/purchasesinboundorder/update`,method: 'post',data: this.$http.adornData(row)});let data = res.dataif (data && data.code !== 0) {row.status = !row.status;return this.$message.error('修改失败!');}this.$message.success('更新成功!');this.getDataList();},
5、定义v-focus
directives: {// 通过自定义指令实现的表单自动获得光标的操作focus: {inserted: function(el) {if (el.tagName.toLocaleLowerCase() == "input") {el.focus()} else {if (el.getElementsByTagName("input")) {el.getElementsByTagName("input")[0].focus()}}el.focus()}},focusTextarea: {inserted: function(el) {if (el.tagName.toLocaleLowerCase() == "textarea") {el.focus()} else {if (el.getElementsByTagName("textarea")) {el.getElementsByTagName("textarea")[0].focus()}}el.focus()}}},