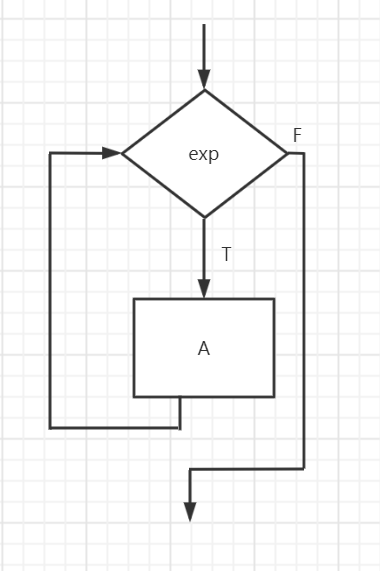
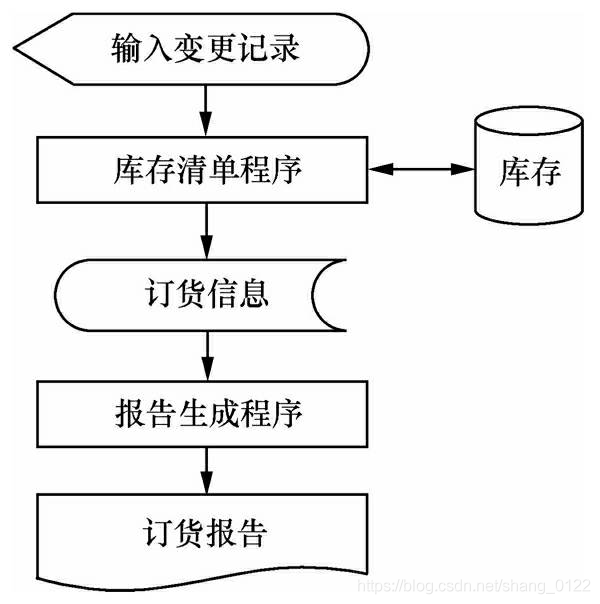
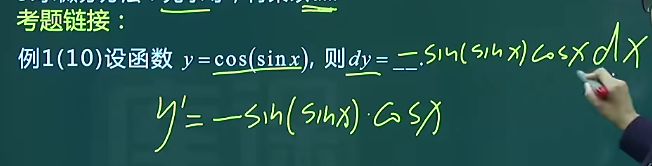今天正式开始学习深度学习,看的书是《深度学习入门——基于python的理论与实现》。
感知机使用阶跃函数作为激活函数,而神经网络使用 sigmoid 函数作为激活函数。
下面分别来用代码实现并绘制阶跃函数和激活函数的图形。
一、阶跃函数
阶跃函数以阈值为界,一旦输入超过了阈值,就会切换输出。
以下的阶跃函数step_function以0为阈值——当输入超过0,则输出1,否则输出0。
import numpy as np
import matplotlib.pylab as pltdef step_function1(x=''):'''简单的阶跃函数——无法接收numpy数组参数'''if x >0:return 1else:return 0def step_function2(x):'''升级版的阶跃函数,这里的参数x为numpy数组'''y = x > 0 # numpy数组中的每个元素都与0比较大小,得到一个布尔型numpy数组return y.astype(np.int) # astype()方法将numpy数组的布尔型转换为int型m = 1
print(step_function1(m))x = np.arange(-5.0,5.0,0.1) # 生成一个numpy数组,范围是(-5.0,5.0),步长为0.1
y = step_function2(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()
运行结果:

【注】
(1)要明白深度学习当中,一定要善于利用 NumPy 数组:
对比这里的 step_function1 和 step_function2 —— step_function1 只能接收普通的数字,调用起来比较死板且麻烦;而 step_function2 可以接收numpy数组,如此,便可充分利用 numpy 的方法来处理许多问题,还可以一次性输入多个数据。
(2)本例涉及到的 numpy 用法如下:
(1)numpy.array([…]) ——>构造一个numpy数组。e.g. x=np.array([2.2, 3.2, 5.2, 4.0])
(2)对numpy数组做运算 ——>数组中的每个元素都做此运算。e.g. 本例中的x>0
(3)numpy数组名.astype(numpy.数据类型) ——>将数组中的元素统一转换为某数据类型。e.g. 本例中y.astype(np.int),将y中的True转换为1,False转换为0
(4)numpy.arange(a,b,l) ——>生成一个numpy数组,范围是(a,b),步长为l。e.g. 本例中x = np.arange(-5.0,5.0,0.1)
(3)其他:
(1)不可以将本例中的两个函数命名为同名函数,python无法处理类似于Java的处理同名异参函数的功能,python只会默认执行最后一个函数,而忽略第一个。
(2)step_function2 还可以写为如下形式,效果完全相同:
def step_function3(x):return np.array(x>0,dtype=np.int)
二、sigmoid函数
sigmoid函数的表达式:h(x) = 1/(1+exp(-x))
【注】
sigmoid函数中 e 的 -x 次方,用NumPy提供的数学方法exp()方法来实现。
用法:numpy.exp(-x) ——>表示 e 的 -x 次方
参数既可以接收普通数字,也可以接收一个numpy数组(利用NumPy数组的广播功能)
import numpy as np
import matplotlib.pyplot as pltdef sigmoid(x):'''sigmoid函数,这里参数x既可以接收普通数字,也可以接收一个numpy数组'''return 1/(1+np.exp(-x))x = np.array([1.0,-1.0,2.0])
print(sigmoid(x)) # 简单调用做测试x = np.arange(-5.0,5.0,0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1) # 指定y轴范围
plt.show()
运行结果:

三、阶跃函数与sigmoid函数的对比
区别:
-
”平滑度“不同
sigmoid函数的图形是一条平滑的曲线,输出随输入的变化而发生连续性的变化;
而阶跃函数的图形在x=0附近发生急剧变化,x>0输出1,x<0输出0。
【注】sigmoid函数的平滑性对于神经网络的学习具有重要意义。
-
返回值不同
阶跃函数只能返回0或1,而阶跃函数可以返回0到1之间若干不同大小的实数。
即,感知机中神经元之间流动的是0或1的二元信号,而神经网络中流动的是连续的实数值信号。
sigmoid函数可以根据输入值的大小相应地调整输出值的大小,而不仅仅是输出是否传递信号(0或1)这一个动作。
共同点:
1. 输出信号的数值范围始终都在0~1之间
不管输入信号有多大或多小,阶跃函数与sigmoid函数的输出信号的数值范围始终都在0~1之间
2. 从宏观上看,二者的图形具有相似的形状
二者的结构都是:输入越小,输出越接近于0(或为0);输出越大,输出越接近于1(或为1)。
即,当输入信号为不重要的信息时,二者均输出较小的值;
当输入信号为重要信息时,二者均输出较大的值。