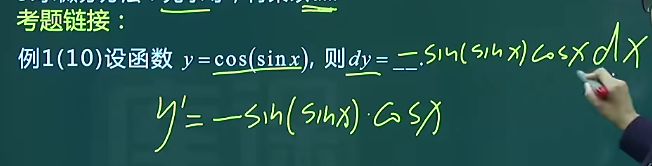x 的平方根
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。也就是说向下取整.
示例 1:
输入: 4
输出: 2
示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,
由于返回类型是整数,小数部分将被舍去
1.先来贴上自己写的,二分法的思想
class Solution {public int mySqrt(int x) {if(x<2) return x;int i=2,j=x/2;long num; //为了防止溢出,选择longwhile(i<=j){int mid=(i+j)/2;num=(long)mid*mid;if(x<num){j=mid-1;}else if(x>num){i=mid+1;}else return mid;} return j;}
}
2.官方题解一
袖珍计算器算法,有兴趣的话可以去了解了解–>袖珍计算器算法
俺是看不懂 (ó﹏ò。)难受
class Solution {public int mySqrt(int x) {if (x < 2) return x;int left = (int)Math.pow(Math.E, 0.5 * Math.log(x));int right = left + 1;return (long)right * right > x ? left : right;}
}3牛顿迭代法
如下截图来源于百度百科


推荐博主和博文(图片的来源)—>马同学高等数学
一看名字就知道是个数学方面的大佬,即便不能全懂,但也能相当了解,拓宽眼界,
∑(っ°Д°;)っ卧槽
切线是曲线的线性逼近,
令f(X)=X^2 -n,任取一点X0, 首先取X0的切线,
---->f(X)=f’(X0) * (X – X0)+f(X0)
…
…
----->f(X)=f’(Xi) * (X – Xi)+f(Xi)
求得X(i+1)=Xi–f(Xi)/f’(Xi),由于f(X)=X^2 -n , f’(Xi)=2Xi ,带入得
则X(i+1)=Xi–(Xi^2-n)/2Xi
= Xi–Xi/2+ n/2Xi
=(Xi+n/Xi)/2
不如草稿纸上看的舒服,建议去手写一下
class Solution {public int mySqrt(int x) {if (x < 2) return x;long r=x;while(r*r>x){r=(r+x/r)/2;}return (int)r;}
}本篇只有一个目的,记录牛顿迭代法,最起码以后我知道数学上有一种方法叫牛顿迭代法,
ᕙ༼ຈلﻝ͜ ຈ༽ᕗI’m the power