Postman全网最详细使用教程

欢迎关注博主公众号「Java大师」, 专注于分享Java领域干货文章, 关注回复「postman」, 获取postman插件和安装程序： http://www.javaman.cn/jszw/postman

一、postman的安装

postman的安装分为两种，通过chrome浏览器插件安装和安装程序安装

在安装了谷歌浏览器后还需要在谷歌网上应用店中下载所需要的Postman插件，不能访问google 应用上商店的朋友可以点击下列地址下载

二、postman发送post、get、delete等请求

1、打开postman进入界面，如下图，左边显示的是历史操作记录，右边为request请求主界面

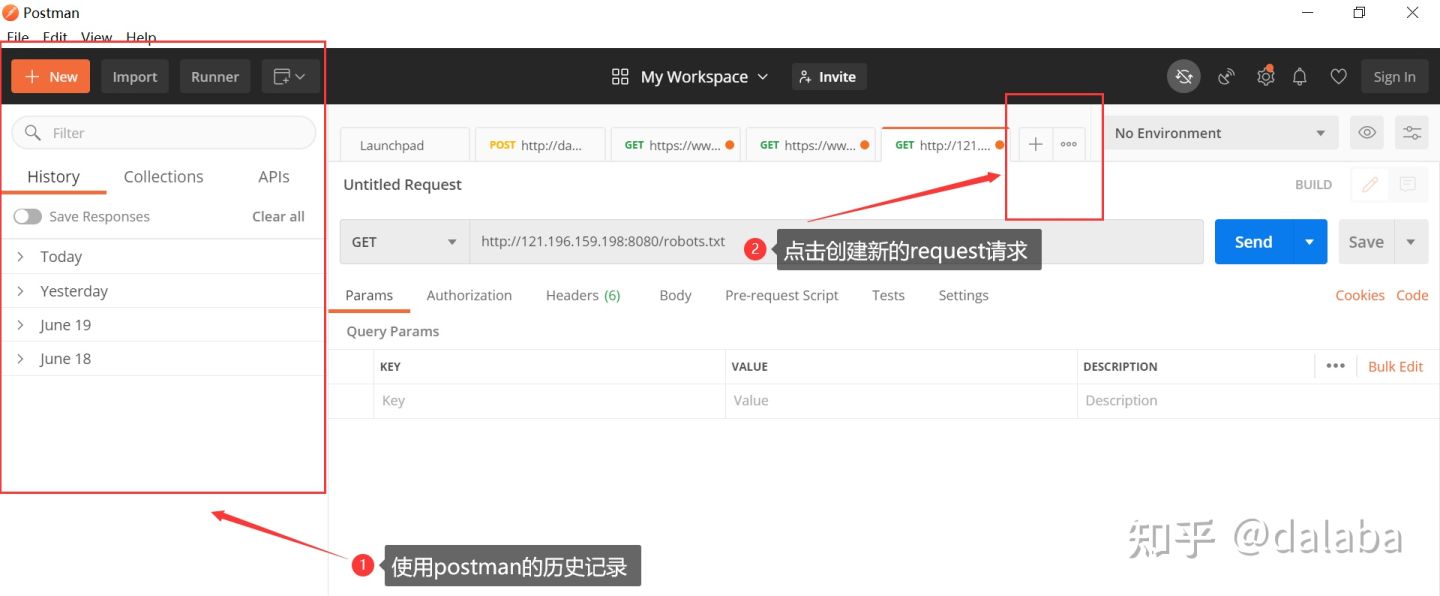
2、点击postman右侧主界面的加号，创建新的request的请求

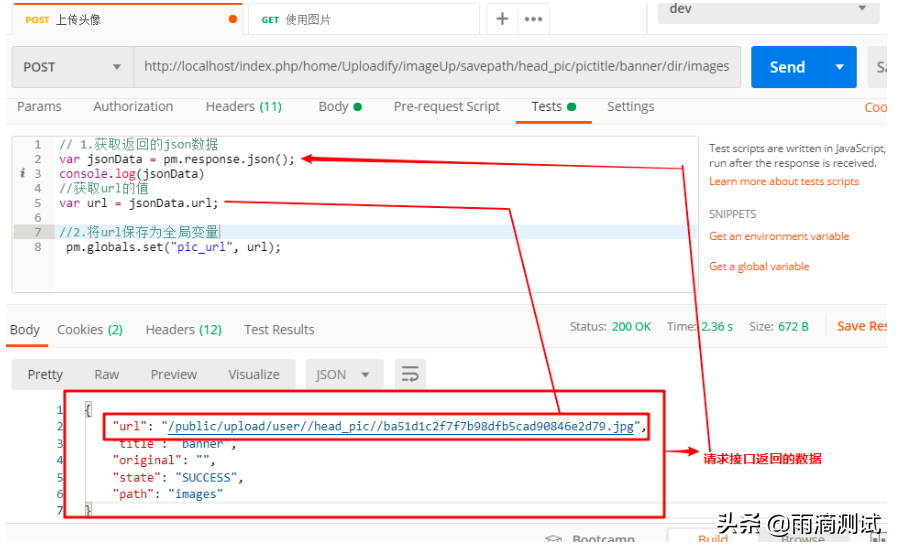
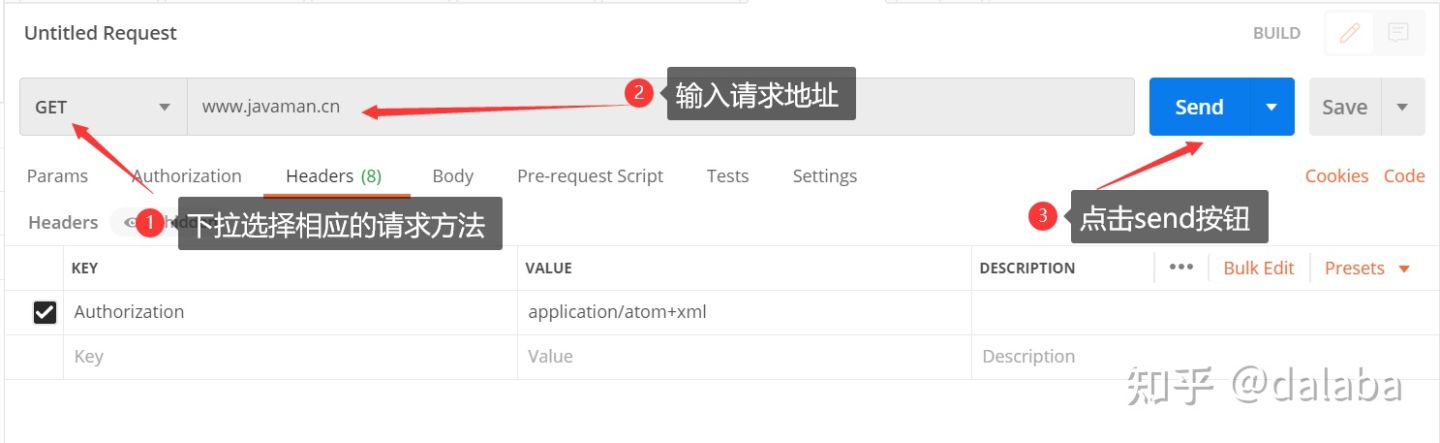
3、选择相应的请求方法、输入请求地址、点击send按钮进行请求的发送

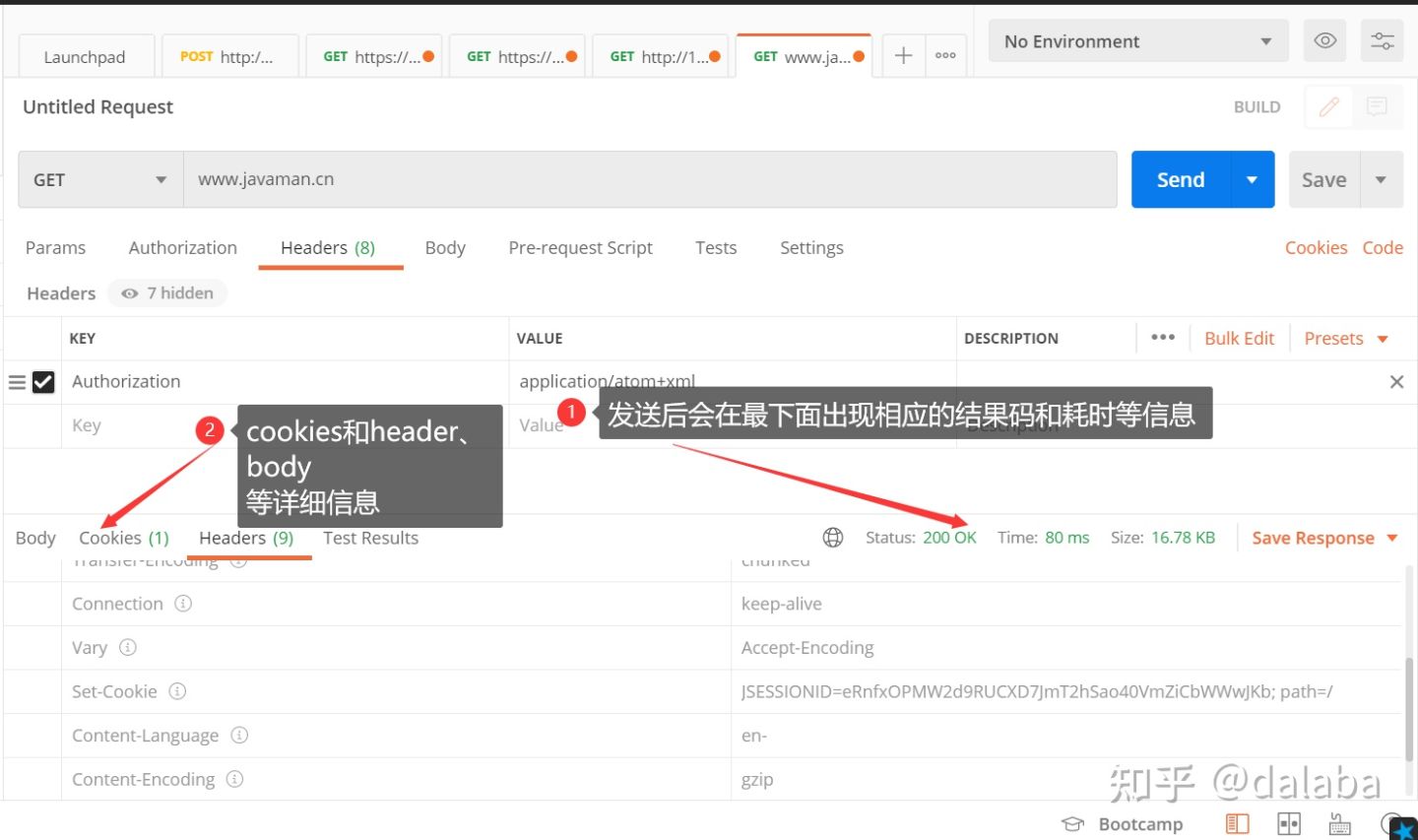
4、发送成功后会出现相应的请求和响应结果码以及耗时等信息

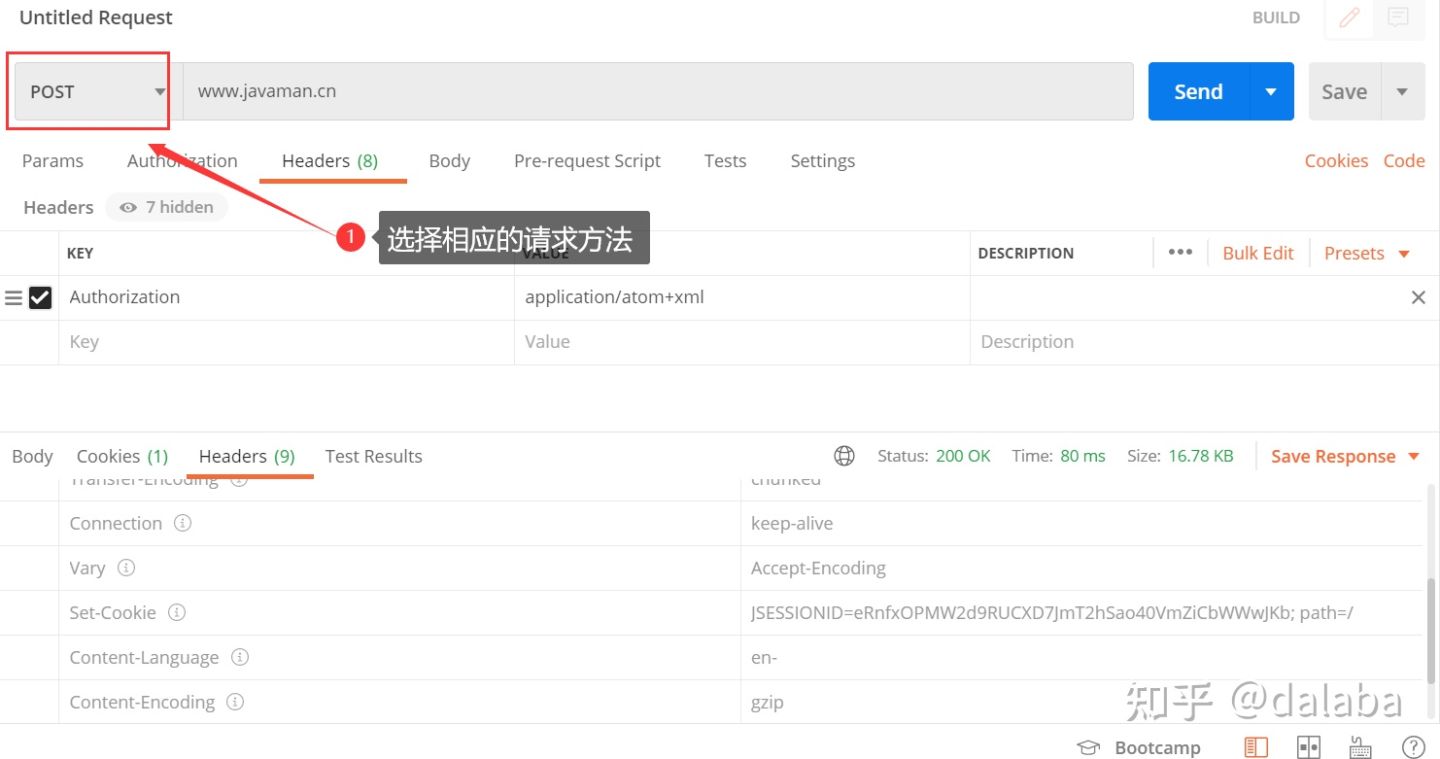
5、其他的如post、put、delete等请求只要选择相应的request请求方法就可以了，如下图

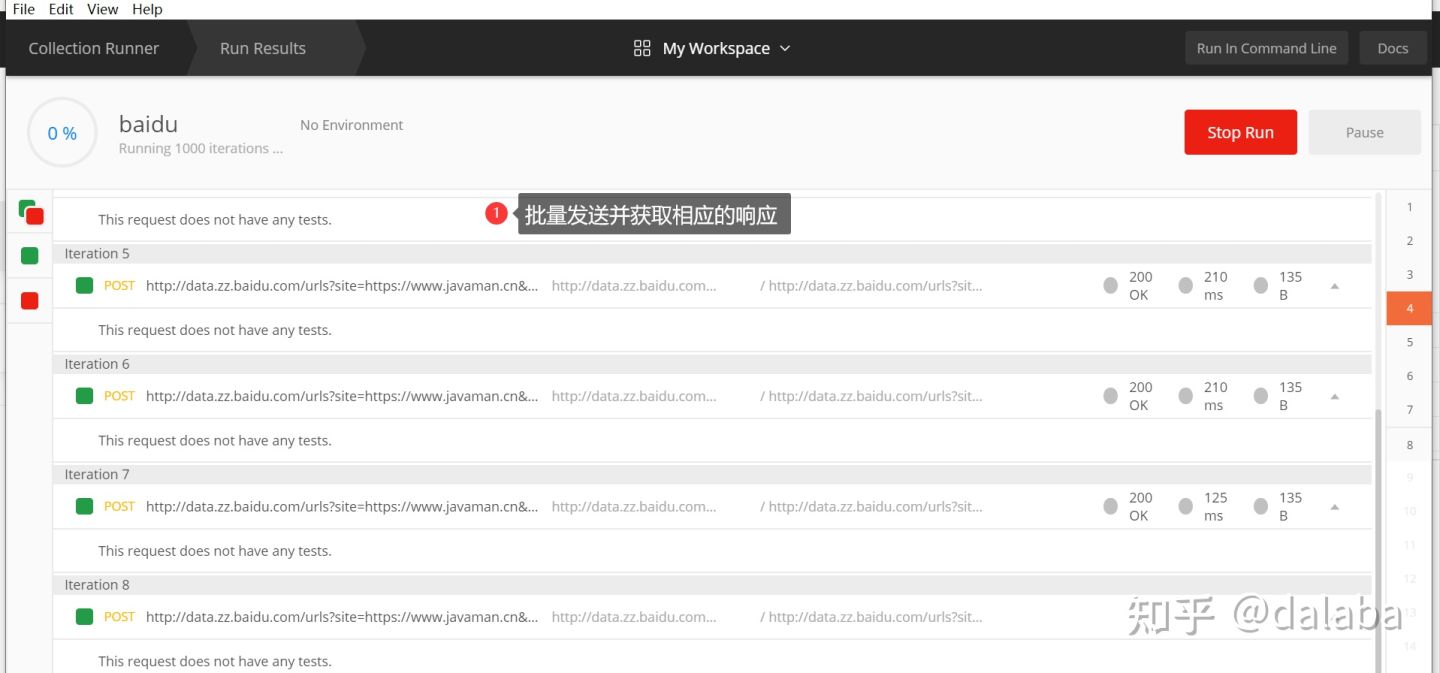
三、postman批量发送请求（百度举例）

有很多情况，需要我们批量进行请求的发送；如果通过程序for循环进行处理当然可以，但是postman已经很智能的帮助我们提供了批量发送请求的方式了，那么我们来看下怎么批量发送

1、点击主界面的new按钮，选择collection

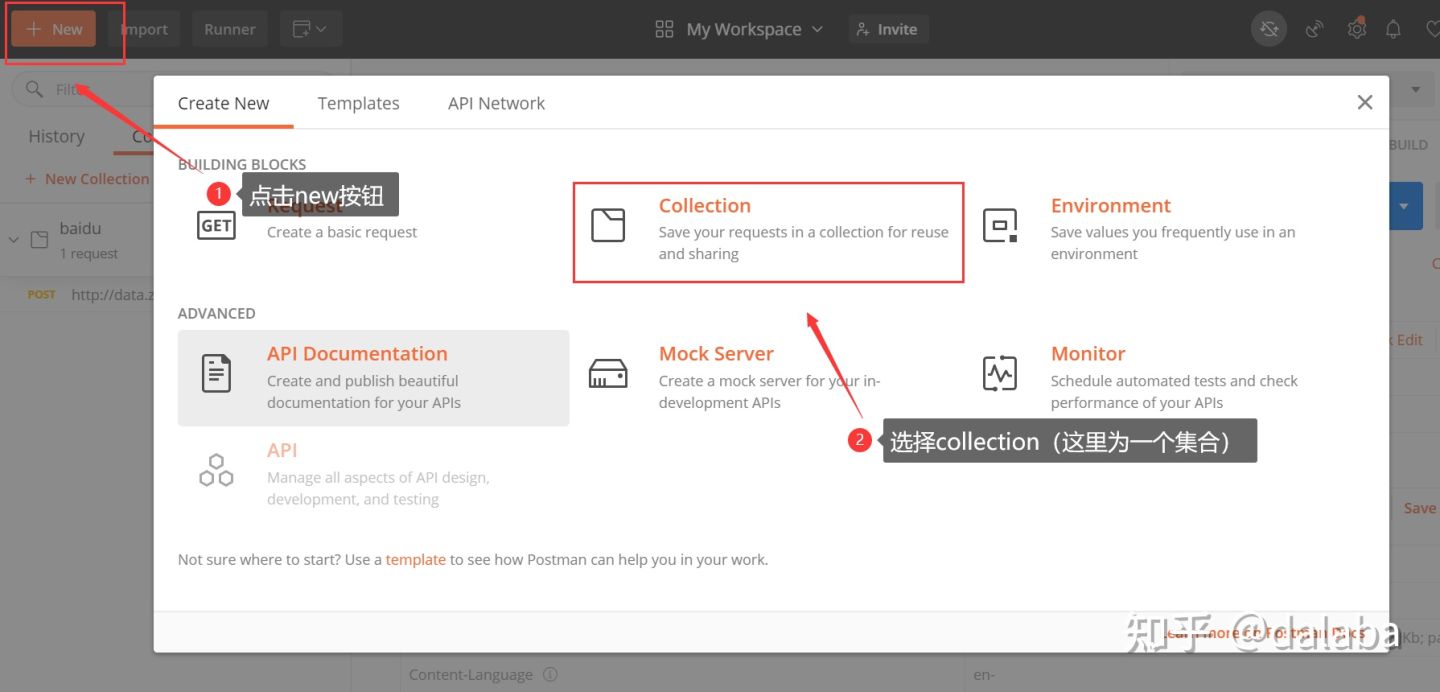
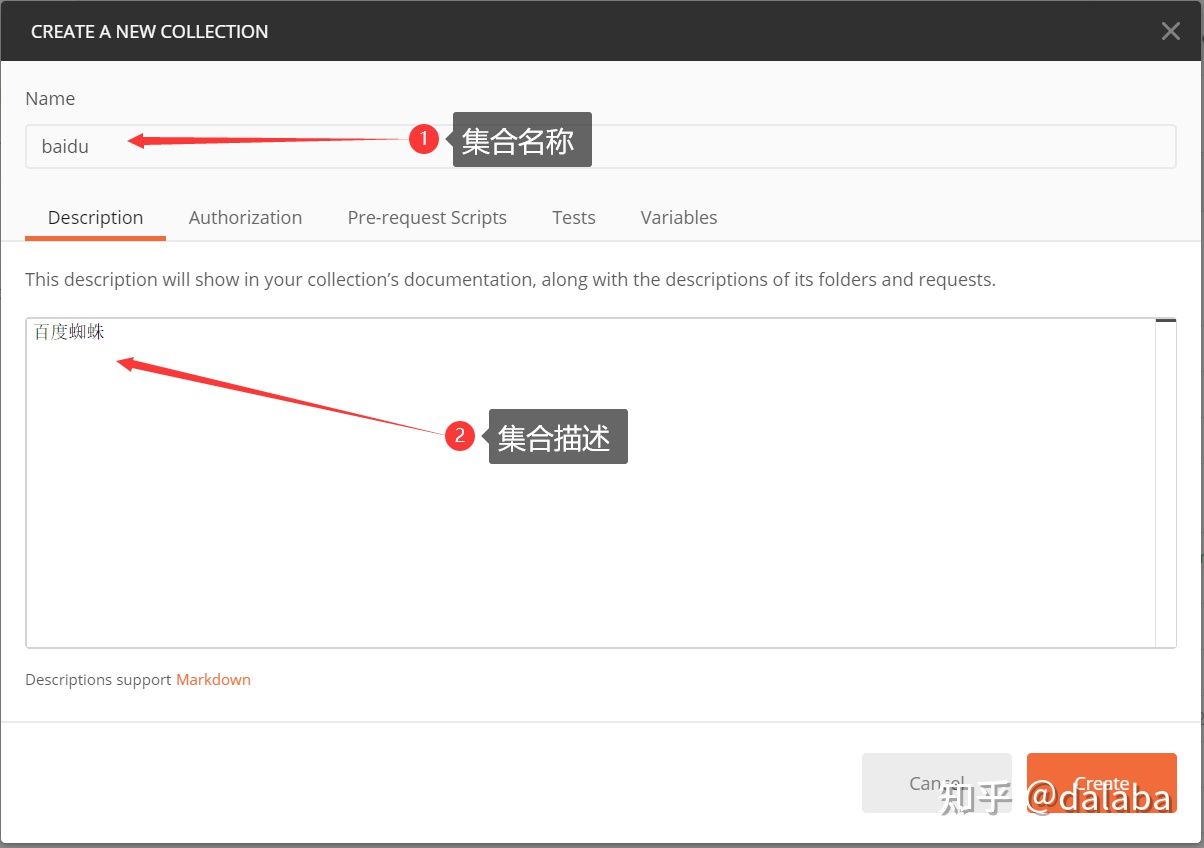
2、进入集合界面，填入集合名称和集合的描述，点击create按钮

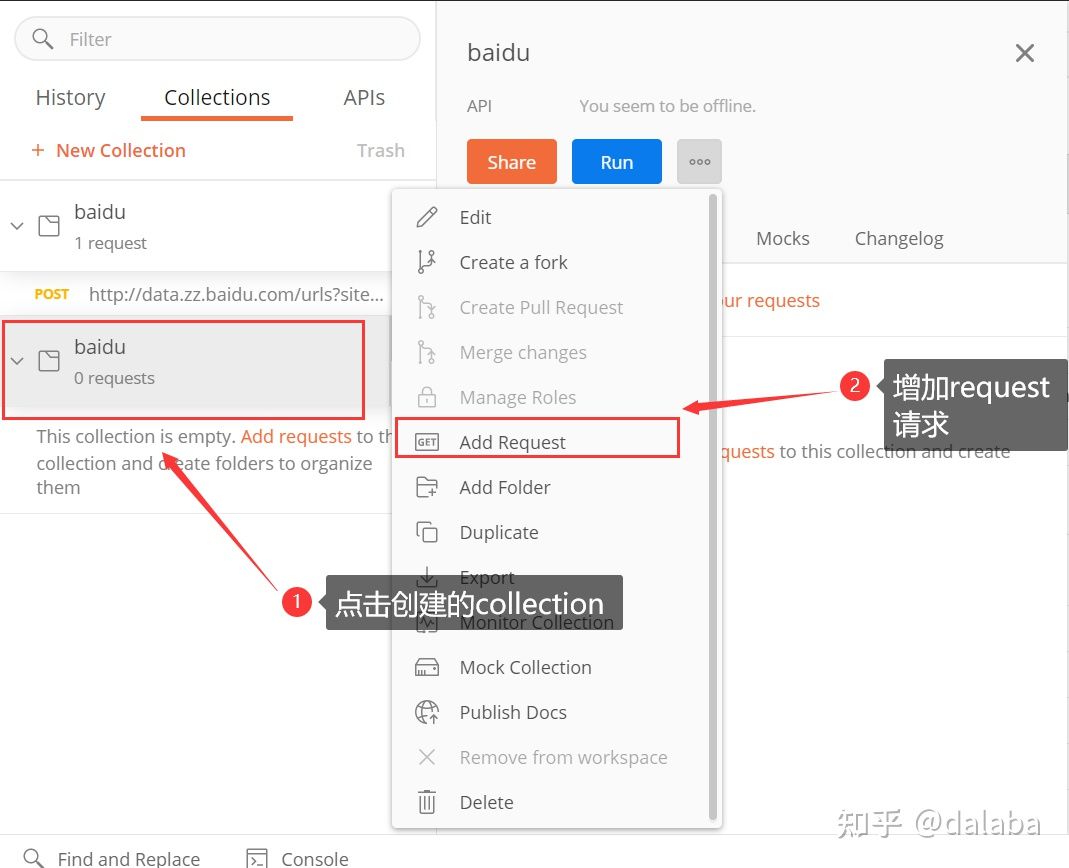
3、选择创建的集合，添加request请求

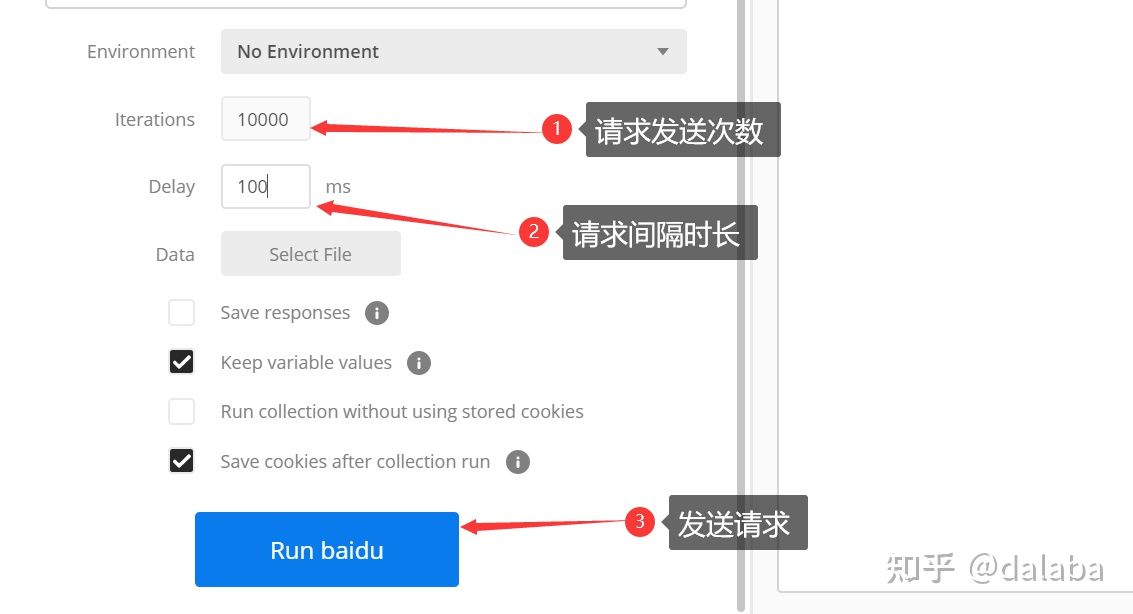
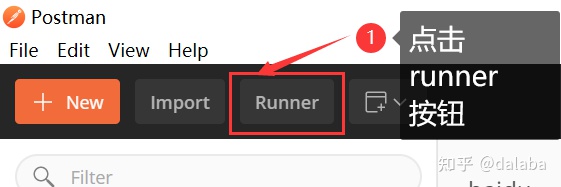
4、批量运行request，点击主界面的runner按钮，进入runner界面

5、输入运行次数和请求发送的间隔时长（毫秒），点击run按钮进行批量发送