蚁群算法讲解python

article/2025/10/3 4:19:13

简介

蚁群算法（Ant Clony Optimization， ACO）作为一个启发式群智能算法，它是由一群无智能或有轻微智能的个体通过相互协作而表现出智能行为，从而为求解复杂问题提供了一个新的可能性。

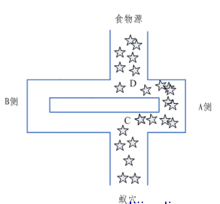
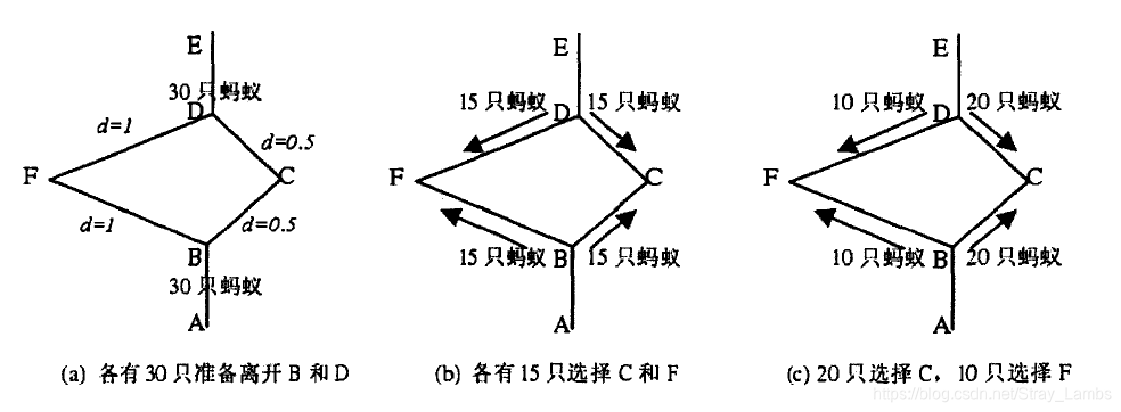
ACO是一种仿生学算法，是由自然界中蚂蚁觅食的行为而启发的。在自然界，蚂蚁觅食过程中，蚁群总能够按照寻找到一条从蚁巢和食物源的最优路径，这也就是蚁群算法的由来。

注：然而蚁群算法去做路径规划和优化智能算法或机器学习算法却不太一样。

路径规划的蚁群算法优化步骤（典型tsp问题）：

  1. 初始化一些参数。α——信息素重要程度因子；β——启发函数重要程度因子；ρ——信息素挥发因子；Q为常数；m为蚁群数量；城市规模num_city；迭代次数iter_max，信息素矩阵\tau _{ij}等。

  2. 计算概率。P_{ij}^{k}(t)=\begin{cases} \frac{\tau _{ij}(t)}{\sum_{s\in allowed_{k}}^{}\tau _{is}(t)}& \text{ if } j= allowed_{k} \\ 0& \text{ if } j\neq allowed_{k} \end{cases}，其中allowed_{k}为第k只蚂蚁后续可以走的城市集合；P_{ij}^{k}(t)为第k只蚂蚁在t时刻从城市i转移到城市j的概率。
  3. 更新信息素浓度。\begin{cases} \tau \left ( t+1 \right )=\left ( 1-\rho \right )\tau _{ij}\left ( t \right )+\sum_{k=1}^{m}\Delta\tau _{ij}^{k} & \text{ if }0< \rho < 1 \\ \Delta \tau _{ij}^{k}=\begin{cases} \frac{Q}{L_{k}}& \text{ if } L_{k}=distant(s_{ij}^{k}) \\ 0& \text{ if } else \end{cases}& \end{cases}，Lk为第k只蚂蚁曾经走过的路径。
  4. 判断是否达到最大迭代次数，达到从而结束算法。
import random
import math
import numpy as np
import matplotlib.pyplot as pltclass ACO(object):def __init__(self, num_city, data):self.m = 50  # 蚂蚁数量self.alpha = 0.5  # 信息素重要程度因子self.beta = 5  # 启发函数重要因子self.rho = 0.1  # 信息素挥发因子self.Q = 1  # 常量系数self.num_city = num_city  # 城市规模self.location = data  # 城市坐标self.Tau = np.zeros([num_city, num_city])  # 信息素矩阵self.Table = [[0 for _ in range(num_city)] for _ in range(self.m)]  # 生成的蚁群self.iter = 1self.iter_max = 500self.dis_mat = self.compute_dis_mat(num_city, self.location)  # 计算城市之间的距离矩阵self.Eta = 10. / self.dis_mat  # 启发式函数self.paths = None  # 蚁群中每个个体的长度# 存储存储每个温度下的最终路径，画出收敛图self.iter_x = []self.iter_y = []# self.greedy_init(self.dis_mat,100,num_city)def greedy_init(self, dis_mat, num_total, num_city):start_index = 0result = []for i in range(num_total):rest = [x for x in range(0, num_city)]# 所有起始点都已经生成了if start_index >= num_city:start_index = np.random.randint(0, num_city)result.append(result[start_index].copy())continuecurrent = start_indexrest.remove(current)# 找到一条最近邻路径result_one = [current]while len(rest) != 0:tmp_min = math.inftmp_choose = -1for x in rest:if dis_mat[current][x] < tmp_min:tmp_min = dis_mat[current][x]tmp_choose = xcurrent = tmp_chooseresult_one.append(tmp_choose)rest.remove(tmp_choose)result.append(result_one)start_index += 1pathlens = self.compute_paths(result)sortindex = np.argsort(pathlens)       # argsort()是将X中的元素从小到大排序后，提取对应的索引index，然后输出到yindex = sortindex[0]result = result[index]for i in range(len(result)-1):s = result[i]s2 = result[i+1]self.Tau[s][s2] = 1self.Tau[result[-1]][result[0]] = 1# for i in range(num_city):#     for j in range(num_city):# return result# 轮盘赌选择def rand_choose(self, p):x = np.random.rand()for i, t in enumerate(p):x -= tif x <= 0:breakreturn i# 生成蚁群def get_ants(self, num_city):for i in range(self.m):start = np.random.randint(num_city - 1)self.Table[i][0] = startunvisit = list([x for x in range(num_city) if x != start])current = startj = 1while len(unvisit) != 0:P = []# 通过信息素计算城市之间的转移概率for v in unvisit:P.append(self.Tau[current][v] ** self.alpha * self.Eta[current][v] ** self.beta)P_sum = sum(P)P = [x / P_sum for x in P]# 轮盘赌选择一个一个城市index = self.rand_choose(P)current = unvisit[index]self.Table[i][j] = currentunvisit.remove(current)j += 1# 计算不同城市之间的距离def compute_dis_mat(self, num_city, location):dis_mat = np.zeros((num_city, num_city))for i in range(num_city):for j in range(num_city):if i == j:dis_mat[i][j] = np.infcontinuea = location[i]b = location[j]tmp = np.sqrt(sum([(x[0] - x[1]) ** 2 for x in zip(a, b)]))dis_mat[i][j] = tmpreturn dis_mat# 计算一条路径的长度def compute_pathlen(self, path, dis_mat):a = path[0]b = path[-1]result = dis_mat[a][b]for i in range(len(path) - 1):a = path[i]b = path[i + 1]result += dis_mat[a][b]return result# 计算一个群体的长度def compute_paths(self, paths):result = []for one in paths:length = self.compute_pathlen(one, self.dis_mat)result.append(length)return result# 更新信息素def update_Tau(self):delta_tau = np.zeros([self.num_city, self.num_city])paths = self.compute_paths(self.Table)for i in range(self.m):for j in range(self.num_city - 1):a = self.Table[i][j]b = self.Table[i][j + 1]delta_tau[a][b] = delta_tau[a][b] + self.Q / paths[i]a = self.Table[i][0]b = self.Table[i][-1]delta_tau[a][b] = delta_tau[a][b] + self.Q / paths[i]self.Tau = (1 - self.rho) * self.Tau + delta_taudef aco(self):best_lenth = math.inf           # math.inf返回浮点正无穷大best_path = Nonefor cnt in range(self.iter_max):# 生成新的蚁群self.get_ants(self.num_city)  # out>>self.Tableself.paths = self.compute_paths(self.Table)# 取该蚁群的最优解tmp_lenth = min(self.paths)tmp_path = self.Table[self.paths.index(tmp_lenth)]# 可视化初始的路径if cnt == 0:init_show = self.location[tmp_path]init_show = np.vstack([init_show, init_show[0]])# 更新最优解if tmp_lenth < best_lenth:best_lenth = tmp_lenthbest_path = tmp_path# 更新信息素self.update_Tau()# 保存结果self.iter_x.append(cnt)self.iter_y.append(best_lenth)print(cnt,best_lenth)return best_lenth, best_pathdef run(self):best_length, best_path = self.aco()return self.location[best_path], best_length# 读取数据
def read_tsp(path):lines = open(path, 'r').readlines()assert 'NODE_COORD_SECTION\n' in linesindex = lines.index('NODE_COORD_SECTION\n')data = lines[index + 1:-1]tmp = []for line in data:line = line.strip().split(' ')if line[0] == 'EOF':continuetmpline = []for x in line:if x == '':continueelse:tmpline.append(float(x))if tmpline == []:continuetmp.append(tmpline)data = tmpreturn datadata = read_tsp('data/st70.tsp')data = np.array(data)
data = data[:, 1:]
# 加上一行因为会回到起点
show_data = np.vstack([data, data[0]])aco = ACO(num_city=data.shape[0], data=data.copy())
Best_path, Best = aco.run()
print(Best)
Best_path = np.vstack([Best_path, Best_path[0]])
plt.plot(Best_path[:, 0], Best_path[:, 1])
plt.title('st70:aco-tsp')
plt.show()

蚁群算法优化智能算法（以优化函数为例）： 

  1. 初始化种群pop_size=100 ，最大迭代次数NGEN=50，信息素挥发因子rou=0.8，Q常量为1。
  2. 随机产生蚂蚁初始位置，计算适应度函数值，设为初始信息素，计算信息素转移概率 
    pi[i] = (t_max - t[i]) / t_max

  3. 依据概率计算下一时刻位置 
     if pi[i] < np.random.uniform(0, 1):self.pop_x[i][j] = self.pop_x[i][j] + np.random.uniform(-1, 1) * lamdaelse:self.pop_x[i][j] = self.pop_x[i][j] + np.random.uniform(-1, 1) * (self.bound[1][j] - self.bound[0][j]) / 2

  4. 信息素更新。 
    t[i] = (1 - rou) * t[i] + Q * self.fitness(self.pop_x[i])

  5. 反复迭代，直到达到最大迭代次数

完整python代码：

import numpy as np
import matplotlib.pyplot as pltclass ACO:def __init__(self, parameters):# 初始化self.NGEN = parameters[0]  # 迭代的代数self.pop_size = parameters[1]  # 种群大小self.var_num = len(parameters[2])  # 变量个数self.bound = []  # 变量的约束范围self.bound.append(parameters[2])self.bound.append(parameters[3])self.pop_x = np.zeros((self.pop_size, self.var_num))  # 所有蚂蚁的位置self.g_best = np.zeros((1, self.var_num))  # 全局蚂蚁最优的位置# 初始化第0代初始全局最优解temp = -1for i in range(self.pop_size):for j in range(self.var_num):self.pop_x[i][j] = np.random.uniform(self.bound[0][j], self.bound[1][j])fit = self.fitness(self.pop_x[i])if fit > temp:self.g_best = self.pop_x[i]temp = fitdef fitness(self, ind_var):"""个体适应值计算"""x1 = ind_var[0]x2 = ind_var[1]x3 = ind_var[2]y = 4*x1 ** 2 + 2*x2 + x3 ** 3return ydef update_operator(self, gen, t, t_max):"""更新算子：根据概率更新下一时刻的位置"""rou = 0.8  # 信息素挥发系数Q = 1  # 信息释放总量lamda = 1 / genpi = np.zeros(self.pop_size)for i in range(self.pop_size):for j in range(self.var_num):pi[i] = (t_max - t[i]) / t_max# 更新位置if pi[i] < np.random.uniform(0, 1):self.pop_x[i][j] = self.pop_x[i][j] + np.random.uniform(-1, 1) * lamdaelse:self.pop_x[i][j] = self.pop_x[i][j] + np.random.uniform(-1, 1) * (self.bound[1][j] - self.bound[0][j]) / 2# 越界保护if self.pop_x[i][j] < self.bound[0][j]:self.pop_x[i][j] = self.bound[0][j]if self.pop_x[i][j] > self.bound[1][j]:self.pop_x[i][j] = self.bound[1][j]# 更新t值t[i] = (1 - rou) * t[i] + Q * self.fitness(self.pop_x[i])# 更新全局最优值if self.fitness(self.pop_x[i]) > self.fitness(self.g_best):self.g_best = self.pop_x[i]t_max = np.max(t)return t_max, tdef main(self):popobj = []best = np.zeros((1, self.var_num))[0]for gen in range(1, self.NGEN + 1):if gen == 1:tmax, t = self.update_operator(gen, np.array(list(map(self.fitness, self.pop_x))),np.max(np.array(list(map(self.fitness, self.pop_x)))))else:tmax, t = self.update_operator(gen, t, tmax)print('############ Generation {} ############'.format(str(gen)))print(self.g_best)print(self.fitness(self.g_best))if self.fitness(self.g_best) > self.fitness(best):best = self.g_best.copy()popobj.append(self.fitness(best))print('最好的位置：{}'.format(best))print('最大的函数值：{}'.format(self.fitness(best)))print("---- End of (successful) Searching ----")plt.figure()plt.title("Figure1")plt.xlabel("iterators", size=14)plt.ylabel("fitness", size=14)t = [t for t in range(1, self.NGEN + 1)]plt.plot(t, popobj, color='b', linewidth=2)plt.show()if __name__ == '__main__':NGEN = 100popsize = 50low = [1, 1, 1]up = [30, 30, 30]parameters = [NGEN, popsize, low, up]aco = ACO(parameters)aco.main()

 效果不好时，大家记得调节参数。

总结：

蚁群算法缺点：

  1. 收敛速度慢
  2. 易于陷入局部最优

参数作用：

  1. 蚂蚁数量：种群数量越多，得到的最优解就越精确,但是会有大量蚂蚁重复路过同一路径,运行时间增多。
  2. alpha  信息素重要程度因子：alpha值过大,蚂蚁选择之前走过的路径可能性就越大,蚁群搜索路径的随机性减弱。alpha值过小,蚁群搜索范围就会减少,易陷入局部最优解。
  3. beta 启发函数因子：beta值增大,蚁群更容易选择局部较短路径,能加快算法的运行速度,但是可能陷入局部最优解。
  4. ruo 信息素挥发因子：当ruo很小的时候，每条路径的残留信息很多，就会反复进行搜索，运算时间增加；ruo很大的时候,会放弃搜索很多有效路径,可能会丢失最优值。


http://chatgpt.dhexx.cn/article/kWQhiLkt.shtml

相关文章

蚁群算法详解（含例程）

蚁群算法详解（含例程）

该篇博客为课程学习的笔记&#xff0c;含一个例子可以帮助理解蚁群算法&#xff0c;主要为理论知识的总结。 蚁群算法详解 1.算法简介2.Ant System(蚂蚁系统)2.1 路径构建2.2 信息素更新 3. 改进的蚁群算法3.1 精英策略的蚂蚁系统(Elitist Ant System, EAS)3.2 基于排列的蚂蚁…
阅读更多...
蚁群算法小结及算法实例（附Matlab代码）

蚁群算法小结及算法实例（附Matlab代码）

目录 1、基本蚁群算法 2、基本蚁群算法的流程 3、关键参数说明 3.1 信息素启发式因子 α 3.2 期望启发因子 β 3.3 信息素蒸发系数 ρ 3.4 蚂蚁数目 m 3.5 信息素强度 Q 对算法性能的影响 3.6 最大进化代数 G 4、MATLAB仿真实例 4.1 蚁群算法求解旅行商问题&#xf…
阅读更多...
蚁群算法代码实现

蚁群算法代码实现

旅行商问题大都是用遗传算法求解&#xff0c;不过蚁群算法比它高效得多&#xff0c;在百度的蚁群算法吧里有人发了个注释清晰的代码&#xff0c;有兴趣的可以去研究一下蚁群算法和模拟退火算法&#xff0c;这两者都可以解决旅行商问题。而关于遗传算法和模拟退火算法&#xff0…
阅读更多...
蚁群算法（ACO）

蚁群算法（ACO）

目录 ACO简介 基本原理 算法步骤 流程图 参数意义 构建路径 更新信息素 实例演示&#xff08;TSP问题&#xff09; ACO简介 蚁群是自然界中常见的一种生物&#xff0c;人们对蚂蚁的关注大都是因为“蚁群搬家&#xff0c;天要下雨”之类的民谚。然而随着近代仿生学的发展&…
阅读更多...
蚁群算法及其应用

蚁群算法及其应用

产生背景 20世纪90年代初&#xff0c;意大利科学家Marco Dorigo等受蚂蚁觅食行为的启发&#xff0c;提出蚁群算法(Ant Colony Optimization&#xff0c;ACO)。 一种应用于组合优化问题的启发式搜索算法。 在解决离散组合优化方面具有良好的性能。 基本思想 信息素跟踪&#…
阅读更多...
蚁群算法原理及python代码实现

蚁群算法原理及python代码实现

本文转载自&#xff1a;https://blog.csdn.net/fanxin_i/article/details/80380733 蚁群算法(AG)是一种模拟蚂蚁觅食行为的模拟优化算法&#xff0c;它是由意大利学者Dorigo M等人于1991年首先提出&#xff0c;并首先使用在解决TSP&#xff08;旅行商问题&#xff09;上。 之后…
阅读更多...
蚁群算法原理以及应用

蚁群算法原理以及应用

关键词：启发式算法 蚁群算法 迭代 正反馈 1.蚁群算法(ant colony algorithm,ACA)起源和发展历程 Marco Dorigo等人在研究新型算法的过程中，发现蚁群在寻找食物时，通过分泌一种称为信息素的生物激素交流觅食信息从而能快速的找到目标，于是在1991年在其博士论文中首次系统地提…
阅读更多...
蚁群算法浅谈

蚁群算法浅谈

本文参考&#xff1a;http://www.cnblogs.com/biaoyu/archive/2012/09/26/2704456.html http://blog.163.com/ykn_2010/blog/static/1420333362012111411258466/ 简介 蚁群算法(ant colony optimization, ACO)&#xff0c;又称蚂蚁算法&#xff0c;是一种用…
阅读更多...
【转载】蚁群算法原理及实现

【转载】蚁群算法原理及实现

转自&#xff1a;https://blog.csdn.net/yy2050645/article/details/80820287 蚁群算法 蚁群算法&#xff0c;也是优化算法当中的一种。蚁群算法擅长解决组合优化问题。蚁群算法能够有效的解决著名的旅行商问题&#xff08;TSP&#xff09;&#xff0c;不止如此&#xff0c;在…
阅读更多...
蚁群算法原理及c++实现

蚁群算法原理及c++实现

参考博客 https://blog.csdn.net/Oudasheng/article/details/84994336 https://blog.csdn.net/wayjj/article/details/72809344#commentsedit https://blog.csdn.net/Oudasheng/article/details/84994336 https://www.cnblogs.com/mahaitao/p/5572095.html https://www.cnblogs…
阅读更多...
10分钟搞懂蚁群算法

10分钟搞懂蚁群算法

蚂蚁几乎没有视力&#xff0c;但他们却能够在黑暗的世界中找到食物&#xff0c;而且能够找到一条从洞穴到食物的最短路径。它们是如何做到的呢&#xff1f; 蚂蚁寻找食物的过程 单只蚂蚁的行为及其简单&#xff0c;行为数量在10种以内&#xff0c;但成千上万只蚂蚁组成的蚁群却…
阅读更多...
蚁群算法的简单理解

蚁群算法的简单理解

蚁群优化算法是意大利学者等人在世纪年代初提出的一种源于生物世界的新型启发式仿生算法。它是从自然界中蚂蚁觅食过程的协作方式得到启发而研究产生的。 在自然界中&#xff0c;蚁群可以在其觅食的过程中逐渐寻找到食物源与巢穴之间的最短路径。单个蚂蚁在运动过程中能够分泌…
阅读更多...
蚁群算法原理及matlab代码实现

蚁群算法原理及matlab代码实现

蚁群算法基本原理&#xff1a; 背景&#xff1a; 在自然界中&#xff0c;生物群体所表现出的智能得到越来越多的关注&#xff0c;许多的群智能优化算法都是通过对群体智能的模拟而实现的。其中模拟蚂蚁群体觅食的蚁群算法成为一种主要的群智能算法。 算法原理&#xff1a; 在…
阅读更多...
蚁群算法介绍

蚁群算法介绍

前言&#xff1a;本篇文章主要讲述蚁群算法以及相关算法的matlab实现 一、蚁群算法 蚁群算法是在20世纪90年代由澳大利亚学者Marco Dorigo等人通过观察蚁群觅食的过程&#xff0c;发现众多蚂蚁在寻找食物的过程中&#xff0c;总能找到一条从蚂蚁巢穴到食物源之间的最短路径。随…
阅读更多...
优化算法3--蚁群算法(原理)

优化算法3--蚁群算法(原理)

1 算法简介 优化问题在科学和工业领域都非常重要。这些优化问题的实际例子有时间表调度、护理时间分配调度、列车调度、容量规划、旅行商问题、车辆路径问题、群店调度问题、组合优化等。为此&#xff0c;开发了许多优化算法。蚁群优化就是其中之一。 蚁群优化(Ant colony op…
阅读更多...
蚁群算法(实例帮助理解)

蚁群算法(实例帮助理解)

1. 算法简介1.1 算法起源1.2 算法应用 2. 基本原理3. 算法设计3.1 算法步骤3.2 参数意义及设置3.3 构建路径3.4 更新信息素浓度3.5 判断是否中止 4. 实例演示&#xff08;TSP问题&#xff09; 1. 算法简介 1.1 算法起源 蚁群算法(ant colony optimization, ACO)&#xff0c;又…
阅读更多...
蚂蚁算法蚁群算法-原理-思路-步骤-程序实现

蚂蚁算法蚁群算法-原理-思路-步骤-程序实现

蚂蚁算法蚁群算法-原理-思路-步骤-程序实现 ❀算法介绍 历史 蚁群优化算法是一种用来在图中寻找优化路径的机率型算法。它由Marco Dorigo于1992年在他的博士论文中提出&#xff0c;其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。蚁群算法是一种模拟进化算法&#xff0c;…
阅读更多...
蚁群算法原理及其实现(python)

蚁群算法原理及其实现(python)

蚁群算法(AG)是一种模拟蚂蚁觅食行为的模拟优化算法&#xff0c;它是由意大利学者Dorigo M等人于1991年首先提出&#xff0c;并首先使用在解决TSP&#xff08;旅行商问题&#xff09;上。 之后&#xff0c;又系统研究了蚁群算法的基本原理和数学模型. 蚁群算法的基本思想: 蚁群…
阅读更多...
智能算法——蚁群算法

智能算法——蚁群算法

1、原理 蚁群算法是受到对真实蚂蚁群觅食行为研究的启发而提出。生物学研究表明&#xff1a;一群相互协作的蚂蚁能够找到食物和巢穴之间的最短路径,而单只蚂蚁则不能。生物学家经过大量细致观察研究发现,蚂蚁个体之间的行为是相互作用相互影响的。蚂蚁在运动过程中,能够在它所…
阅读更多...
蚁群算法理解与实现

蚁群算法理解与实现

蚁群算法&#xff0c;也是优化算法当中的一种。蚁群算法擅长解决组合优化问题。蚁群算法能够有效的解决著名的旅行商问题&#xff08;TSP&#xff09;&#xff0c;不止如此&#xff0c;在其他的一些领域也取得了一定的成效&#xff0c;例如工序排序问题&#xff0c;图着色问题&…
阅读更多...
推荐文章

Copyright @ 2022~2023