参考博客
https://blog.csdn.net/Oudasheng/article/details/84994336
https://blog.csdn.net/wayjj/article/details/72809344#commentsedit
https://blog.csdn.net/Oudasheng/article/details/84994336
https://www.cnblogs.com/mahaitao/p/5572095.html
https://www.cnblogs.com/Horizon-asd/p/12723886.html
https://blog.csdn.net/chen10217/article/details/100762552

一、原理

1. 蚂蚁觅食行为

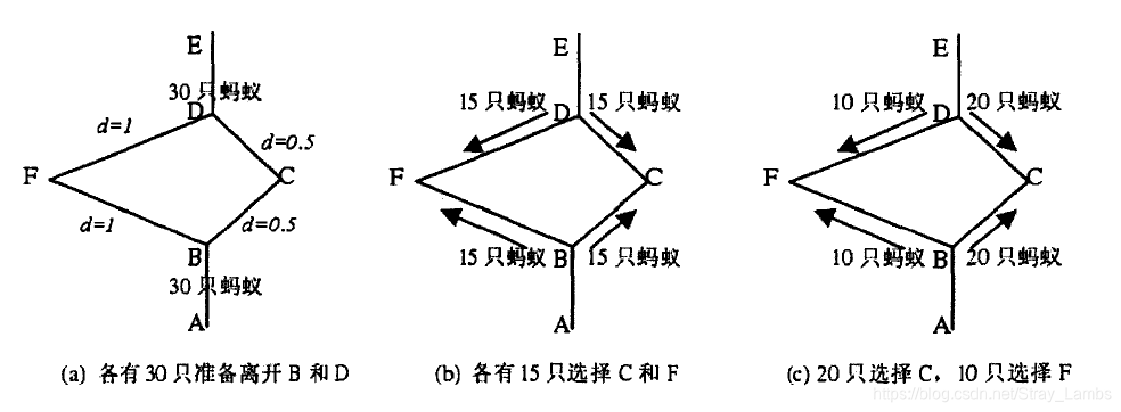
蚁群在寻找食物时，总能找到一条蚁穴到食物的最短路径，并且能随着环境的变化而更新最优路径。究其原因，是因为蚂蚁在运动过程中，会在所经过路径上留下一种称为信息素（pheromone）的物质，其他蚂蚁在运动中可以感知到这种物质，并以此来指导自己的运动方向。
蚁群的这种行为表现出一种信息正反馈现象：某一路径上走过的蚂蚁越多，则后来者选择该路径的概率越大。

2.蚁群算法

又称蚂蚁算法，是一种基于群体智能的算法，用来在图中寻找优化路径的概率型。它由Marco Dorigo于1992年在他的博士论文中提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。在解决实际问题时，人工蚁群相较于自然蚁群有一定的记忆能力，可记住已访问过的节点，其次人工蚁群在选择路径时依照一定规律，并不是盲目的。蚁群算法常用来解决路径规划等离散优化问题，如旅行商问题（TSP）、指派问题、调度问题。

2,1 特点

正反馈：可较快发现较优解。
分布式：基于种群的进化算法，本质具有并行性，易于并行实现。
启发式搜索：反映搜索中的的先验性和确定性因素（如距离）强度。
鲁棒性强：不易受某个个体影响。

2.2 算法流程（以TSP问题为例）

TSP问题：一商人去n个城市销货，所有城市走一遍再回到起点，使所走路程最短。

初始化相关参数：蚁群规模、信息素因子、启发函数因子、信息素挥发因子、信息素常数和最大迭代次数等。将城市信息读入程序并进行预处理，即将城市间信息转化为矩阵。
随机将蚂蚁放入不同出发点，计算每个蚂蚁的下一步要访问的城市，直到有蚂蚁访问完所有城市。
计算每个蚂蚁经过的路径长度Lk，记录当前迭代次数下的最优解（访问完所有城市且路径长度最短），更新各条路径上的信息素浓度。
断是否达到最大迭代次数，若否则返回步骤2，若是则顺序执行。
输出最优路径和相关指标，如运行时间和迭代次数。

2.3 相关公式

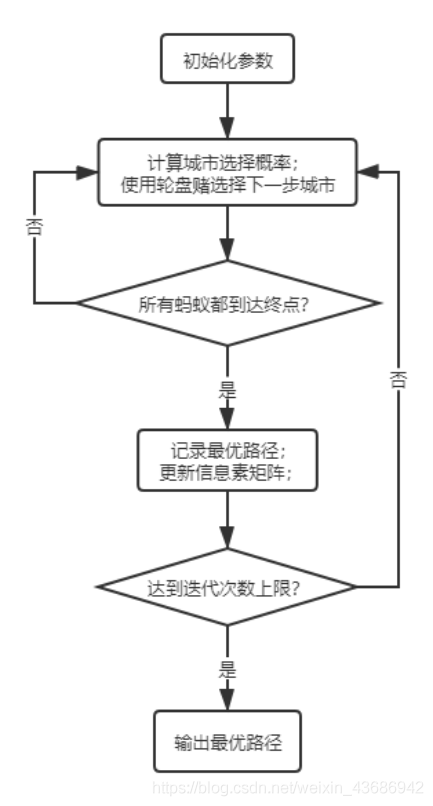
在这里插入图片描述

2.4 流程图

在这里插入图片描述

三、例子

试设计一个并行算法，求下图中一个源点到其他定点的最短路径。（VS2019+Eigen）
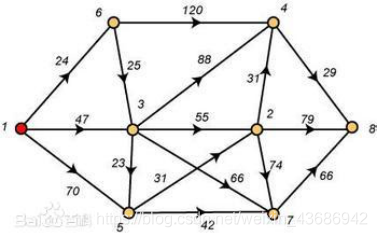
在这里插入图片描述

3.1 关键代码

数据结构：

将蚂蚁设置为一个结构体，包含所在位置、禁忌表、所走路径和是否到达终点标志四项内容。为了便于计算，将信息素、启发信息与距离信息分别在8*8的矩阵中存放，这样可以调用Eigen库直接进行矩阵计算，达到更新信息素的目的。
城市也设为一个结构体，包含城市编号和选择概率两项内容。这里将城市设置为结构体，主要是考虑到在选择下一步行进城市时，要先计算选择概率再通过轮盘赌来确定下一步城市，轮盘赌时需要将城市编号与其选择概率一一对应。
具体代码部分如下：

struct ant                 //蚂蚁结构体
{int loc;               //位置int tabu[cityNum];     //禁忌表int antPath[pathNum];  //走过的路bool flag;             //是否到达终点7
};
struct ant ants[antNum];   //蚁群typedef Matrix<double, 8, 8> Matrix8d;
Matrix8d dist;             //距离矩阵
Matrix8d pher;             //信息素矩阵
Matrix8d nextPher;         //下一代信息素矩阵
Matrix8d insp;             //启发信息矩阵struct city                //城市结构体
{int num;               //编号double prob;           //选择概率
};
struct city cityProb[cityNum];    //可到达城市组
double lineCityProb[cityNum];     //线性化 可到达城市的选择概率

城市选择方式

当蚂蚁k选择下一步要去的城市时，有以下几个步骤：

对照蚂蚁k的禁忌表，求出下一步所有可去的城市各自的选择概率(概率计算见公式(1)）；
线性化所有可去城市的概率，生成介于0~1之间的随机数（线性化概率的目的是实现轮盘赌）；
使用轮盘赌方法选择下一步要去的城市。
概率计算与轮盘赌选择对应代码片如下：

//轮盘赌选择下一步行进城市
int citySelect(int k, int f)
{int c = 0;//记录蚂蚁可行进的城市个数//1、计算可行进的各城市 选择概率for (int m = 0; m < cityNum; m++){//若城市（i,j）之间有路且j不在蚂蚁k的禁忌表中，则计算概率if (dist(ants[k].loc, m) != -1 && !ifCityInTabu(m, k)){cityProb[c].num = m;cityProb[c].prob = citySelProb(k, m);c++;}}//2、线性化选择概率for (int m = 0; m < c; m++){for (int n = m; n >= 0; n--){lineCityProb[m] += cityProb[n].prob;}}//3、产生随机数选择城市double r = rand() / double(RAND_MAX);int j = 0;   //选取的目标城市for (int m = 0; m < cityNum; m++){if (r <= lineCityProb[m]){j = cityProb[m].num;updateAnt(k, j);if (j == f)ants[k].flag = 1;  //若蚂蚁k下一步城市为目的地城市，则修改标志return j;}}
}

信息素更新

因为将信息素存入矩阵，所以在计算时较为简单，具体分为如下几步：

计算信息素增量矩阵：
for k = 1 to m do (遍历蚁群)
for j = 1 to n do (遍历蚂蚁k的行走路径)
　　计算蚂蚁k在路径(i, j)对应的信息素增量（见公式（3））;
更新路径(i, j)在上一轮的信息素增量；
　 end for
end for
计算更新后的信息素矩阵：
信息素挥发系数*信息素矩阵+信息素增量矩阵（见公式（2））。
对应代码片如下：

 void updatePher()
{for (int i = 0; i < antNum; i++){if(ants[i].flag == 1)  //只对到达目的点的蚂蚁 所走过路径 更新信息素for (int j = 0; j < pathNum; j++){if (ants[i].antPath[j] == -1 || ants[i].antPath[j + 1] == -1)break;elsenextPher(ants[i].antPath[j], ants[i].antPath[j + 1])+= pQ / getAntLen(ants[i]);}}nextPher = pVol * pher + nextPher;
}

3.2 运行结果

参数设置

const int cityNum = 8;     //城市数量
const int pathNum = 16;    //路径数量
const int antNum = 12;     //蚂蚁数量（1.5倍城市数量）
const double pVol = 0.3;   //信息素挥发系数 0.2~0.5
const int pQ = 10;         //信息素强度 10~1000
const double pImp = 3;     //信息素相对重要性 1~4
const double qImp = 4;     //启发信息相对重要性 3~4.5
const int gen = 100;       //迭代次数 100~500

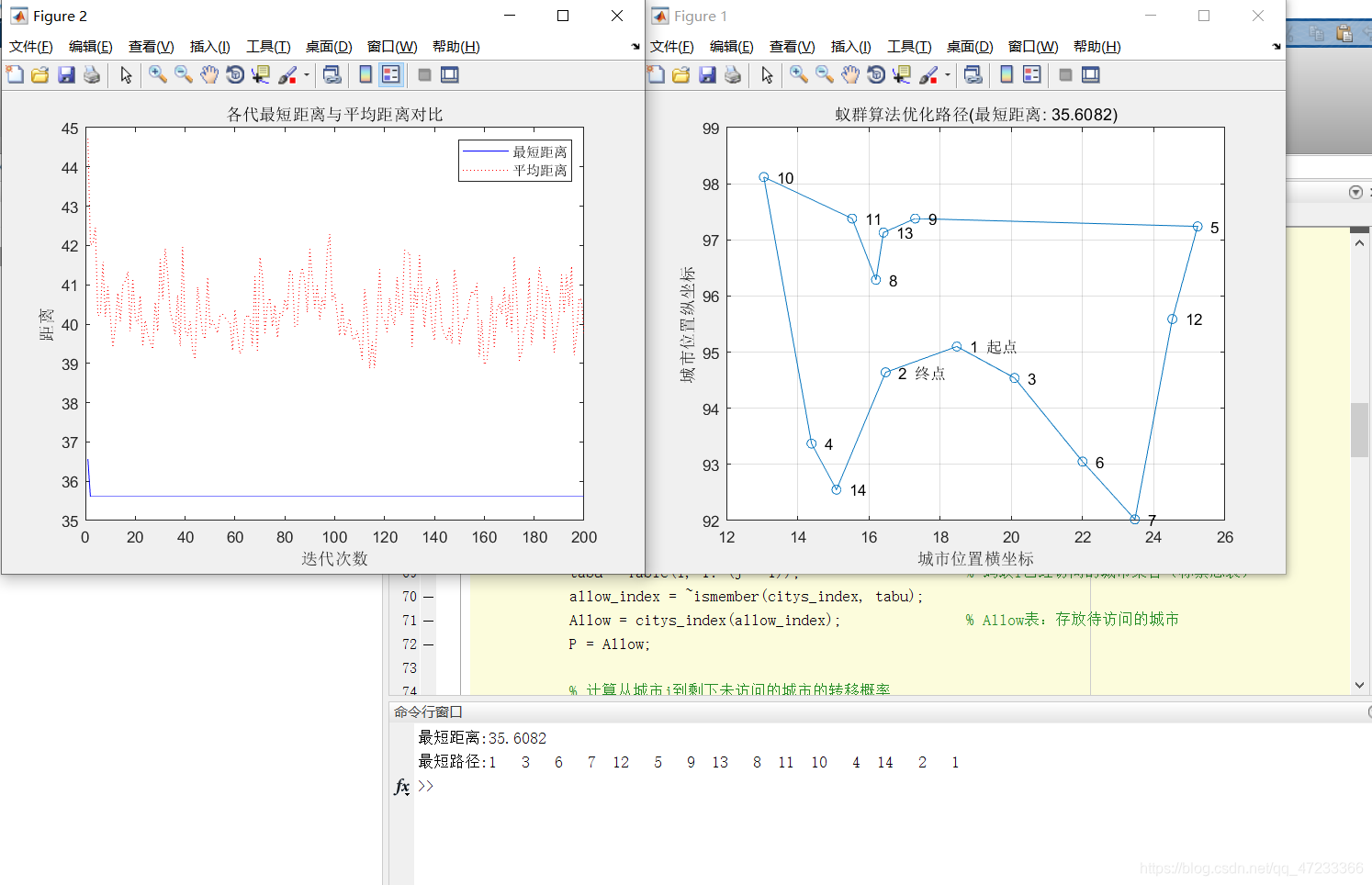
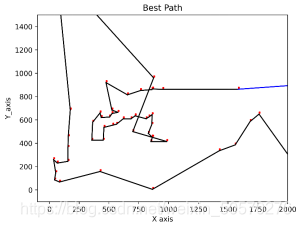
运行结果

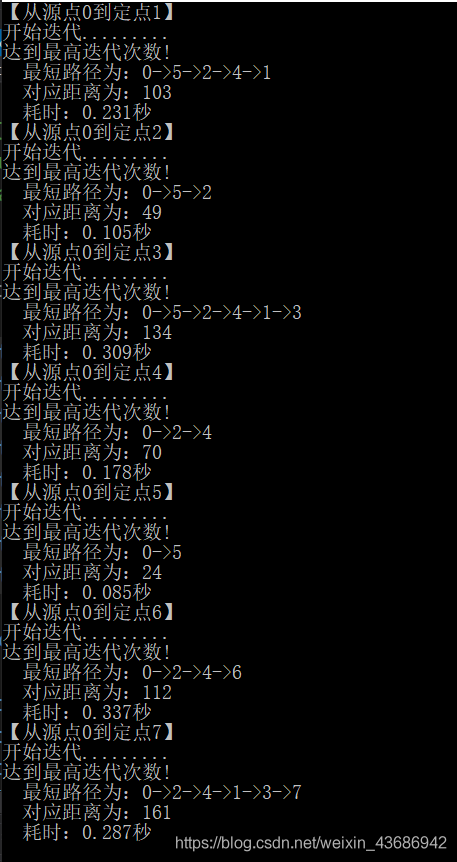
在这里插入图片描述

问题

各项参数初始值虽然知道设置范围，但因为不够理解参数如何影响迭代的结果，参数设定主要依靠猜测。
代码运行后，发现回归太早，不符合蚁群算法回归较慢（200~500）的特点，后经过检查，发现是计算蚂蚁k在路径(i,j)上的信息素增量时，将除数Lk理解成了路径(i，j) 的距离，但实际上应该为蚂蚁k本次迭代中做走过路径距离之和。经修改后，可以符合蚁群算法回归较慢的特点。
只计算源点到某一个定点时，代码没有问题，循环结算到每个顶点最短路径时，有时运行会报如下错误，有时不会，不太明白。

源码

#include<iostream>
#include<Eigen\Dense>
#include<stdlib.h>
#include<time.h>
#include<math.h>using namespace Eigen;
using namespace std;/* 功能：此代码使用蚁群算法计算源点0 ~ 其他定点的最短路径author：yuzeweidate：2020/12/19
*/#define CLOCK_PER_SEC ((clock_t)1000)const int cityNum = 8;     //城市数量
const int pathNum = 16;    //路径数量
const int antNum = 12;     //蚂蚁数量（1.5倍城市数量）
const double pVol = 0.3;   //信息素挥发系数 0.2~0.5
const int pQ = 10;         //信息素强度 10~1000
const double pImp = 3;     //信息素相对重要性 1~4
const double qImp = 4;     //启发信息相对重要性 3~4.5
const int gen = 100;       //迭代次数 100~500struct ant                 //蚂蚁结构体
{int loc;               //位置int tabu[cityNum];     //禁忌表int antPath[pathNum];  //走过的路bool flag;             //是否到达终点7
};
struct ant ants[antNum];   //蚁群typedef Matrix<double, 8, 8> Matrix8d;
Matrix8d dist;             //距离矩阵
Matrix8d pher;             //信息素矩阵
Matrix8d nextPher;         //下一代信息素矩阵
Matrix8d insp;             //启发信息矩阵struct city                //城市结构体
{int num;               //编号double prob;           //选择概率
};
struct city cityProb[cityNum];    //可到达城市组
double lineCityProb[cityNum];     //线性化 可到达城市的选择概率clock_t start, finish;     
double duration;void initAnts();                  
void initCityProb();              
void initMarix();   
bool ifCityInTabu(int, int);
int citySelect(int, int);
void updateAnt(int, int);
double citySelProb(int, int);
int getAntLen(ant);
int getBestPath();
void printBestPath(int, int);
void updatePher();
void evolution();int main()
{srand((unsigned)time(NULL));evolution();
}//蚁群初始化
void initAnts()
{//初始化禁忌表与行走路线for (int i = 0; i < antNum; i++){for (int j = 0; j < cityNum; j++){ants[i].tabu[j] = -1;}for (int j = 0; j < pathNum; j++){ants[i].antPath[j] = -1;}}//将蚂蚁放入城市for (int i = 0; i < antNum; i++){//ants[i].loc = rand() % 8;ants[i].loc = 0;//出发点都在起点ants[i].tabu[0] = ants[i].loc;ants[i].antPath[0] = ants[i].loc;ants[i].flag = 0;}
}//初始化城市选择概率数组
void initCityProb()
{for (int i = 0; i < cityNum; i++){cityProb[i].num = -1;cityProb[i].prob = 0;lineCityProb[i] = 0;}
}//初始化距离、信息素、启发信息矩阵
void initMarix()
{dist = Matrix8d::Constant(8, 8, -1);dist(0, 2) = 47;dist(0, 4) = 70;dist(0, 5) = 24;dist(1, 3) = 31;dist(1, 6) = 74;dist(1, 7) = 79;dist(2, 1) = 55;dist(2, 3) = 88;dist(2, 4) = 23;dist(2, 6) = 66;dist(3, 7) = 29;dist(4, 1) = 31;dist(4, 6) = 42;dist(5, 2) = 25;dist(5, 3) = 120;dist(6, 7) = 66;pher = Matrix8d::Zero();nextPher = Matrix8d::Zero();insp = Matrix8d::Zero();for (int i = 0; i < 8; i++){for (int j = 0; j < 8; j++){if (dist(i, j) != -1){insp(i, j) = 1 / dist(i, j);//启发信息为距离的倒数pher(i, j) = 1;             //信息素浓度初始值为1}}}
}//轮盘赌选择下一步行进城市
int citySelect(int k, int f)
{int c = 0;//记录蚂蚁可行进的城市个数//1、计算可行进的各城市 选择概率for (int m = 0; m < cityNum; m++){//若城市（i,j）之间有路且j不在蚂蚁k的禁忌表中，则计算概率if (dist(ants[k].loc, m) != -1 && !ifCityInTabu(m, k)){cityProb[c].num = m;cityProb[c].prob = citySelProb(k, m);c++;}}//2、线性化选择概率for (int m = 0; m < c; m++){for (int n = m; n >= 0; n--){lineCityProb[m] += cityProb[n].prob;}}//3、产生随机数选择城市double r = rand() / double(RAND_MAX);int j = 0;   //选取的目标城市for (int m = 0; m < cityNum; m++){if (r <= lineCityProb[m]){j = cityProb[m].num;updateAnt(k, j);if (j == f)ants[k].flag = 1;  //若蚂蚁k下一步城市为目的地城市，则修改标志return j;}}
}//更新蚂蚁信息
void updateAnt(int k, int l)
{ants[k].loc = l;for (int i = 0; i < cityNum; i++)if (ants[k].tabu[i] == -1){ants[k].tabu[i] = l;break;}for (int i = 0; i < pathNum; i++)if (ants[k].antPath[i] == -1){ants[k].antPath[i] = l;break;}
}//蚂蚁k从当前城市i选择下一步行进城市为j市的概率
double citySelProb(int k, int j)
{double a, b, c, prob;a = b = c = prob = 0;int i = ants[k].loc;a = pow(pher(i, j), pImp) + pow(insp(i, j), qImp);for (int m = 0; m < cityNum; m++){if (dist(i, m) != -1 && !ifCityInTabu(m, k)){b = pow(pher(i, m), pImp) + pow(insp(i, m), qImp);c += b;}}prob = a / c;return prob;
}//判断城市j是否在蚂蚁k的禁忌表中
bool ifCityInTabu(int j, int k)
{for (int i = 0; i < cityNum; i++){if (j == ants[k].tabu[i]){return 1;//break;}}return 0;
}//计算路径长度
int getAntLen(struct ant a)
{int len = 0;for (int j = 0; j < pathNum; j++){if (a.antPath[j] == -1 || a.antPath[j + 1] == -1)break;elselen += dist(a.antPath[j], a.antPath[j + 1]);}return len;
}//计算最优路径对应的蚂蚁编号
int getBestPath()
{int d[antNum];int min;int k;  //蚂蚁k的路线到达目的地节点最短for (int i = 0; i < antNum; i++){d[i] = -1;}for (int i = 0; i < antNum; i++){d[i] = getAntLen(ants[i]);}min = d[0];k = 0;for (int i = 1; i < antNum; i++){if (d[i] < min && ants[i].flag == 1)  // 最优路径只从到达目标点的蚂蚁中筛选{min = d[i];k = i;}}return k;
}//打印最优路径、最短距离
void printBestPath(int k, int f)
{cout << "  最短路径为：";for (int i = 0; i < pathNum; i++){if (ants[k].antPath[i] == -1)break;cout << ants[k].antPath[i];if (ants[k].antPath[i+1] != -1)cout << "->";}cout << endl;cout << "  对应距离为：" << getAntLen(ants[k]) << endl;
}//更新信息素矩阵
void updatePher()
{for (int i = 0; i < antNum; i++){if(ants[i].flag == 1)  //只对到达目的点的蚂蚁 所走过路径 更新信息素for (int j = 0; j < pathNum; j++){if (ants[i].antPath[j] == -1 || ants[i].antPath[j + 1] == -1)break;elsenextPher(ants[i].antPath[j], ants[i].antPath[j + 1])+= pQ / getAntLen(ants[i]);}}nextPher = pVol * pher + nextPher;
}//迭代
void evolution()
{for (int f = 1; f < cityNum; f++){cout << "【从源点0到定点" << f << "】" << endl;cout << "开始迭代........." << endl;//初始化参数initAnts();initMarix();int g = 0; //当前代数start = clock();while (g < gen){//1、蚁群内所有蚂蚁都到达目的地int p = 0; //蚁群前进步数while (p < pathNum){for (int i = 0; i < antNum; i++){if (ants[i].flag == 1)//到达目的地continue;citySelect(i, f);initCityProb();}p++;}if (g == gen - 1){cout << "达到最高迭代次数!" << endl;printBestPath(getBestPath(), f);}//3、更新信息素矩阵updatePher();//4、初始化蚁群；更新信息素矩阵initAnts();pher = nextPher;nextPher = Matrix8d::Zero();g++;}finish = clock();duration = ((double)finish - start) / CLOCK_PER_SEC;cout << "  耗时：" << duration << "秒" << endl;}}