蚁群算法介绍

前言：本篇文章主要讲述蚁群算法以及相关算法的matlab实现

一、蚁群算法

蚁群算法是在20世纪90年代由澳大利亚学者Marco Dorigo等人通过观察蚁群觅食的过程，发现众多蚂蚁在寻找食物的过程中，总能找到一条从蚂蚁巢穴到食物源之间的最短路径。随后他们在蚂蚁巢穴到食物源之间设置了一个障碍，一段时间以后发现蚂蚁又重新走出了一条到食物源最短的路径。通过对这种现象的不断研究，最后提出了蚁群算法。蚁群算法在解决旅行商问题（即TSP问题）时，取得了比较理想的结果。

二、基本人工蚁群算法原理

当蚂蚁外出寻找食物或者返回到巢穴时候，都会释放一种特殊的信息素来标示进行的轨迹，有了这种信息传递机制，蚂蚁才能顺利的返回，进一步研究发现，这种信息素不仅能被统同一个蚁群的其他蚂蚁感受到，而且其强度也能被其他蚂蚁所感知到，蚂蚁会倾向于向信息素浓度高的路径移动，而在移动的过程中又会留下新的信息素。这样，经过蚂蚁越多的路径其信息素浓度也会越来越高，最后，几乎所有的蚂蚁都会走信息素浓度最高的城市，就会在蚂蚁巢穴与食物源之间形成一条最短的取食路径。M.Dorigo将真实蚁群的这种行为抽象为人工蚁群算法，在一方面将真实蚁群中最重要的信息机制赋予给了人工蚁群，另一方面让人工蚁群具备了真实蚁群所不具备的一些其他特征。

运用人工蚁群算法求解TSP问题时的基本原理是：将m个蚂蚁随机地放在多个城市，让这些蚂蚁从所在的城市出发，n步（一个蚂蚁从一个城市到另外一个城市为1步）之后返回到出发的城市。如果m个蚂蚁所走出的m条路经对应的中最短者不是TSP问题的最短路程，则重复这一过程，直至寻找到满意的TSP问题的最短路径为止。为了说明这一个算法下面用一个算法流程图来表示一下：

三、人工蚁群算法的数学模型

（一）算法的相关参数

在算法中用到的变量比较多，而每个变量的对算法最终收敛的结果影响程度也不一样，在这里把一些重要的参数说明一下。

$\tau _{ij}$ ：城市i和城市j之间边 $e_{ij}$ 上信息素的残留强度

$\Delta\tau _{ij}$ ：一次循环后边 $e_{ij}$ 上信息素的增量

$\Delta \tau_{ij}^{k}$ ：一次循环之后蚂蚁k对边 $e_{ij}$ 上信息素的贡献量

$\eta _{ij}$ ：城市i，j之间的能见度，反映了由城市i转移到城市j的启发程度

$d_{ij}$ ：城市i到城市j之间的距离

$p_{ij}^{k}$ ：蚂蚁k从当前所在的城市到下一个城市去的概率

$tabu(k)$ ：禁忌表，用于存放第k只蚂蚁已经走过的城市

$Q$ ：信息素总量，信息素总信息量为蚂蚁循环一周后向经过路径释放信息素的总量

$\rho$ ：信息素残留系数，由于蚂蚁释放的信息量回随着时间的转移而逐渐挥发，以至于路径上的信息素不能无限递增，该系数太小时会降低算法的全局搜素能力，过大时容易使算法陷入局部最优，影响全局搜素能力。

$m$ ：蚂蚁总数，在TSP问题中，每次循环当中，每只蚂蚁所走出的每条路径为TSP问题的候选解，m只蚂蚁一次循环所走出来的m条路经为TSP问题的一个解子集，所以这个解子集越大则算法的全局搜索能力越强，但是过大会使算法的收敛速度降低。如果m太小的话，算法也很容易就陷入局部最优，过早的出现停滞现象，（ps：王老师讲过曾经见到一个学生在论文中让一个蚂蚁去跑路径，老师开玩笑说，估计把这只蚂蚁就给累死了）所以选择合理的蚂蚁总数是非常重要的。

$\alpha$ ：信息启发因子，反映了蚂蚁在从城市i向城市j移动时，这两个城市之间道路上所累积的信息素在指导蚂蚁选择城市j的程度，即蚁群在路径搜素中随即性因素作用的强度。

$\beta$ ：期望值启发式因子，反映了蚂蚁在从城市i向城市j转移时候期望值 $\eta _{ij}$ 在指导蚁群搜素中的相对重要程度。其大小反映了蚁群在道路搜素中的先验性、确定性等因素的强弱， $\alpha$ 、 $\beta$ 的大小也会影响算法的收敛性。

(二) 算法过程中的关键步骤

1、上面讲了蚂蚁在选择下一个要转移的城市时候是基于概率选择的，当然这个概率不是随机概率，而是其中的一些参数来决定。假定在t时刻，蚂蚁从目前所在的i城市要选择转移去的下一个j城市，概率大小为 $p_{ij}^{k}$ ：

$p_{ij}^{k}(t)=\left\{\begin{matrix} & \frac{\tau_{ij}^{k}\eta _{ij}^{\beta }}{\sum_{s\in allowed_{k}}\tau_{is}^{k}(t)\eta_{is}^{\beta}(t)} &j\in allowed_{k} \\ \\ &0 &otherwise \end{matrix}\right.$

其中 $allowed_{k}$ 表示允许蚂蚁k下一步可容许去的城市的集合， $\tau_{ij}^{\alpha}$ 为边 $e_{ij}$ 上的信息素因数， $\eta_{ij}^{\beta}$ 为城市i，j间能见度因数。至于这个过程具体是怎么实现的，在程序中会有相关的源码。

2、对任意两个城市i，j之间道路对应的边 $e_{ij}$ 信息素增量按照下式进行：

$\left\{\begin{matrix} &\tau_{ij}(t+1)=\rho\tau_{ij}(t)+\Delta \tau_{ij}(t,t+1)\\ \\&\Delta\tau_{ij}(t,t+1)=\Sigma_{k=1}^{m}\Delta\tau_{ij}^{k}(t,t+1) \end{matrix}\right.$

其中， $\Delta\tau_{ij}^{k}(t,t+1)$ 为蚂蚁k对边 $e_{ij}$ 上所贡献的信息素增量， $\Delta\tau_{ij}(t,t+1)$ 是经过边 $e_{ij}$ 的所有蚂蚁对边 $e_{ij}$ 的信息素量贡献， $\rho$ 为信息素残留系数。对于 $\Delta\tau_{ij}^{k}(t,t+1)$ 的调整方式不同，可以将蚁群算法分为三种模型：蚁密模型、蚁量模型和蚁周模型。

2.1 蚁密模型

在蚁密模型当中，每一只蚂蚁在经过城市i,j时，对该边 $e_{ij}$ 所贡献的信息素增量为常量，每个单位长度是Q：

$a$

2.2 蚁量模型

在蚁量模型中，一只蚂蚁k在经过城市i,j之间边 $e_{ij}$ 时，对该边所贡献的信息素增量为变量，即每单位长度上为 $Q/d_{ij}$ ，它与城市i,j之间的路径长度 $d_{ij}$ 有关，具体为：

$\Delta\tau_{ij}^{k}(t,t+1)=\left\{\begin{matrix} &Q/d_{ij} &e_{ij}\\ & 0 & otherwise \end{matrix}\right$

2.3 蚁周模型

上述两种模型，对两城市之间边 $e_{ij}$ 上信息素贡献的增量在蚂蚁k经过边的同时完成，而蚁周模型对边 $e_{ij}$ 信息素的增量是在本次循环结束时才进行更新调整。一只蚂蚁在经过城市i，j时对边 $e_{ij}$ 上贡献的增量为每单位长度 $Q/L_{k}$ ， $L_{k}$ 为蚂蚁在本次循环走出路径的长度。

$\Delta\tau_{ij}^{k}(t,t+1)=\left\{\begin{matrix} &Q/L_{k} &e_{ij}\\ &0 &otherwise \end{matrix}\right$

本文章就是基于蚁周模型来实现的，介绍完上述的几个关键步骤以后，就要用matlab来实现了。

四、算法的matlab实现

下面给出了matlab实现代码，其中的注释都是自己看懂了之后加上的，

%算法的第一步是先初始化
clear 
m=50;                                   %蚂蚁总数
alpha=1;                                %信息度启发因子
beta=2;                                 %期望值启发式因子
Rho=0.6;                                %信息素挥发因子 
NC_max=100;                             %最大循环次数
Q=80;                                   %信息素增量     
C=[5.326,2.558;4.276,3.452; 4.819,2.624; 3.165,2.457;0.915,3.921;4.637,6.026; 1.524,2.261;3.447,2.111;3.548,3.665; 2.649,2.556;4.399,1.194;4.660,2.949; 1.479,4.440; 5.036,0.244;2.830,3.140;1.072,3.454;5.845,6.203;0.194,1.767;1.660,2.395;2.682,6.072];%20个城市
% 初始化
n=size(C,1);                            %表示n个城市
D=zeros(n,n);                           
for i=1:nfor j=1:nif i~=j                         %表示同一个城市之间的距离不存在D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;elseD(i,j)=eps;end% D(j,i)=D(i,j);end
end
Eta=1./D;                               %城市与城市之间的能见度，在基于概率转移时用到这个参数
Nc=1;                                   %循环计数器
Tau=ones(n,n);                          %信息素浓度矩阵——n*n的单位阵  
Tabu=zeros(m,n);                        %禁忌表  ——m*n的零阵
Road_best=zeros(NC_max,n);              %每次循环最佳路径 最大循环次数*n个城市零阵
Roadlength_best=inf.*ones(NC_max,1);    %每次循环最佳路径的长度  最大循环次数*1 单位阵 
Roadlength_ave=zeros(NC_max,1);         %每次循环的路径的平均值
%将蚂蚁随机分布在n个城市
while Nc<=NC_max                        %小于最大循环次数就继续执行randpos=[];                        for i=1:(ceil(m/n))                 %分多少次将蚂蚁分布完randpos=[randpos,randperm(n)];  %循环产生的是20个城市的随机数，都在一行endTabu(:,1)=(randpos(1,1:m));         %取前m个城市编号
%每只蚂蚁基于概率选择转移去下一个j城市    for j=2:n                           %从第二个城市开始选择for i=1:m                      visited=Tabu(i,1:(j-1));    %表示已经经过的城市，初始化是出发城市J=zeros(1,(n-j+1));         %存放还没有经过的城市  1*19.....1 零阵P=J;                        Jc=1;                      for k=1:n                   if length(find(visited==k))==0  %查找已经经过的城市里面有没有kJ(Jc)=k;            %没有的话，就把城市k记录进未经过城市矩阵里面Jc=Jc+1;           endend
%计算待选城市的概率for k=1:length(J)            P(k)=(Tau(visited(end),J(k))^alpha)*(Eta(visited(end),J(k))^beta);%目前经过的城市到下一个所有城市的概率大小endP=P/sum(P);%按照概率选取下一个城市Pcum=cumsum(P);              select=find(Pcum>=rand);     to_visit=J(select(1));      Tabu(i,j)=to_visit;          endendif Nc>=2                           Tabu(1,:)=Road_best(Nc-1,:);    end
%记录本次迭代最佳路线L=zeros(m,1);for i=1:mR=Tabu(i,:);                      %第一只蚂蚁的路线赋给矩阵Rfor j=1:(n-1)                     L(i)=L(i)+D(R(j),R(j+1));     %每一只蚂蚁所走的路径长度endL(i)=L(i)+D(R(1),R(n));           %加上最后一个点到起始点的路径endRoadlength_best(Nc)=min(L);           %本次循环的所有路径中的最短路径放在Roadlength_best中pos=find(L==Roadlength_best(Nc));     %找出最短路径的所有蚂蚁Road_best(Nc,:)=Tabu(pos(1),:);       %只取第一只蚂蚁的路径Roadlength_ave(Nc)=mean(L);           %本次循环所有路径的平均值Nc=Nc+1;                              % 跟新信息素delta_Tau=zeros(n,n);                for i=1:m                             for j=1:(n-1)delta_Tau(Tabu(i,j),Tabu(i,j+1))=delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);enddelta_Tau(Tabu(i,n),Tabu(i,1))=delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);endTau=(1-Rho).*Tau+delta_Tau;          %这里运用的是蚁周模型          
% 禁忌表清零                                 Tabu=zeros(m,n);                   
end
pos=find(Roadlength_best==min(Roadlength_best));
shortest_route=Road_best(pos(1),:);
shortest_length=Roadlength_best(pos(1));figure(1)
subplot(1,2,1)
% subplot(1,2,1)
N=length(R);
scatter(C(:,1),C(:,2));
hold on
plot([C(shortest_route(N),1),C(shortest_route(1),1)],[C(shortest_route(N),2),C(shortest_route(1),2)],'g');
hold on
for ii=2:Nplot([C(shortest_route(ii-1),1),C(shortest_route(ii),1)],[C(shortest_route(ii-1),2),C(shortest_route(ii),2)],'g');hold on
end
grid on
title('TSP问题优化结果');
xlabel('x')
ylabel('y')
subplot(1,2,2)
plot(Roadlength_best)
hold on
plot(Roadlength_ave)
grid on
title('平均距离与最短距离')
legend('Roadlength\_best','Roadlength\_ave')
xlabel('cycle-index')
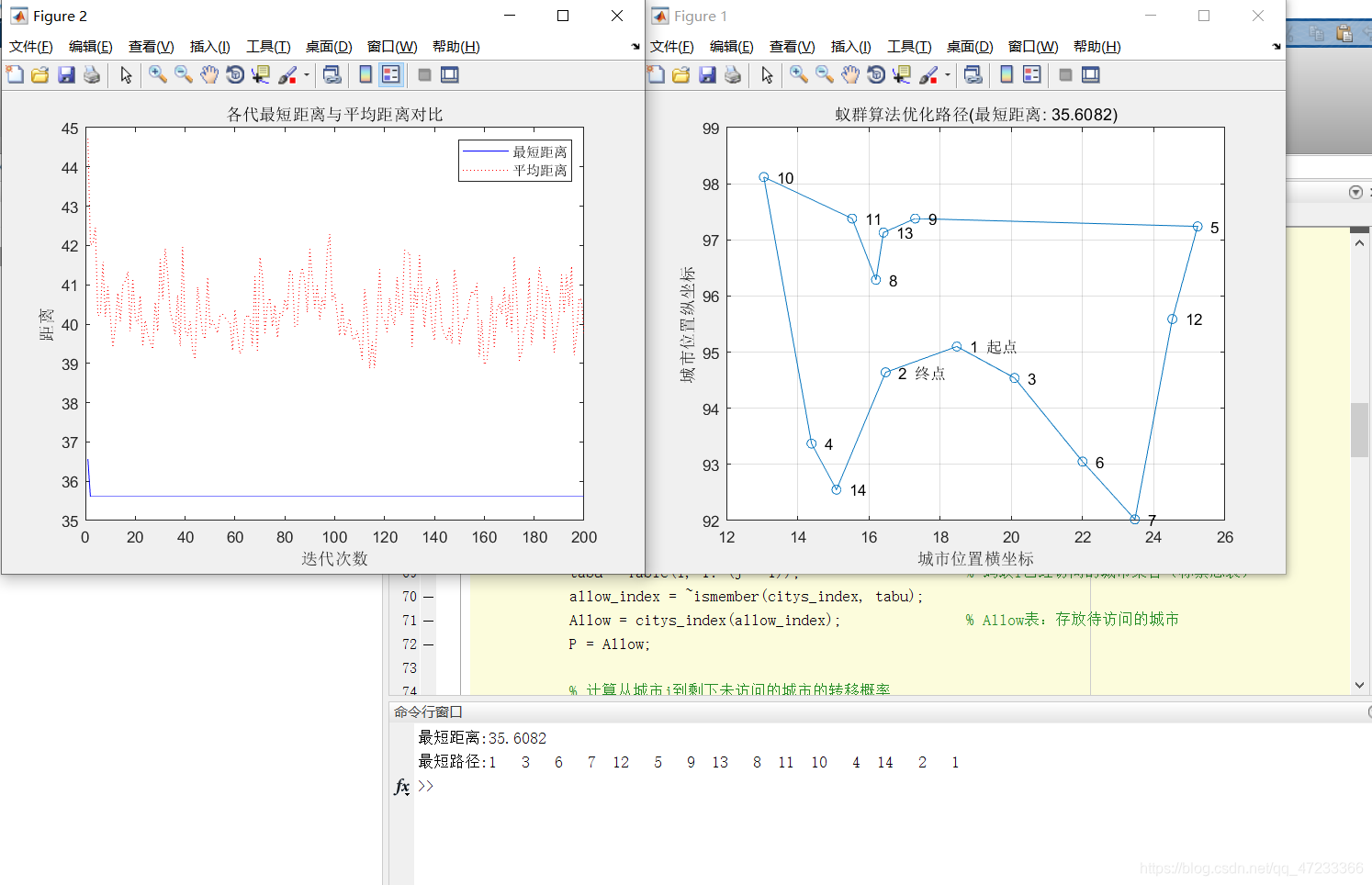
ylabel('length')

经过100次循环，对20个城市求最优路径，结果是23.70，执行之后的效果图如下：