蚁群优化算法是意大利学者等人在世纪年代初提出的一种源于生物世界的新型启发式仿生算法。它是从自然界中蚂蚁觅食过程的协作方式得到启发而研究产生的。
在自然界中,蚁群可以在其觅食的过程中逐渐寻找到食物源与巢穴之间的最短路径。单个蚂蚁在运动过程中能够分泌出一种被称作信息素的化学物质,这种物质能够被蚂蚁所感知,并分辨出其浓度,以此来指导自己倾向于朝着信息素强度高的方向运动。这种倾向是概率的,信息素浓度越高,概率越高,但蚂蚁仍然有可能选择信息素浓度低的路径。这样当外部条件改变,出现一条新的更短的路径的时候,蚁群不会因为一条路径上的高信息素浓度而放弃发现更短的路径。路径上的信息素浓度会被蒸发,当路径上长时间无蚂蚁经过,信息素浓度会自然降低。通过信息素,蚁群在觅食过程中就表现出一种复杂的正反馈现象。蚂蚁个体之间通过信息素进行间接的通信和协作。当某条路径相对其他路径长度越短时,该路径上单位时间内经过的蚂蚁就会越多,该路径上积累的信息素也就越多。而较多的信息素会引导更多的蚂蚁选择这条路径。更多的蚂蚁选择这条路径并经过后又会在该路径上积累更多的信息素,如此循环反复,就使得最后大多数蚂蚁都选择相同的且较短的路径。因而当路径的长度互不相同时,蚂蚁最终会收敛到较短的路径上。但即使路径长度相同,也会由于信息的积累速度不同而引导蚂蚁倾向于其中的一条路径,但其收敛的速度会变慢。
蚁群优化算法就是根据蚁群觅食活动时表现出来的规律,建立的一个利用群体智能进行相互协作,优化搜索的模型。虽然每个个体智能有限,能力很低,但通过群体的高效协作可以解决对于个体而言无法解决的问题。相对于其它的各类智能启发式搜索算法,蚁群算法具有其独特的优越性。它在一系列完全组合优化问题的求解中取得了卓有成效的结果,其中的典型代表有旅行商问题、指派问题以及作业调度等经典组合优化问题。
简单来说:
1、蚂蚁在运动过程中可以分泌信息素,且蚂蚁个体之间通过信息素进行间接的通信和协作;
2、信息素可以被其他蚂蚁识别,且蚂蚁通过概率朝着高浓度的信息素的方向前进(一种正反馈现象);
3、信息素会被蒸发,若长时间没有蚂蚁经过,信息素将会降低。
蚁群算法的基本原理:
其协作方式的本质是
①信息素浓度越浓的路径,被蚂蚁选中的概率也就越大,即蚂蚁路径概率选择机制,这是蚁群搜索求解的基础机制;
②如果路径越短,那么路径上面的信息素就积累得越快,浓度也就会增长得越快,这是蚁群信息素的更新机制;
③蚂蚁能够感应到信息素浓度的不同,蚂蚁之间通过信息素进行通信,告诉其他蚂蚁自己走过的路径,即蚁群协同工作机制。
蚁群寻找食物的流程:
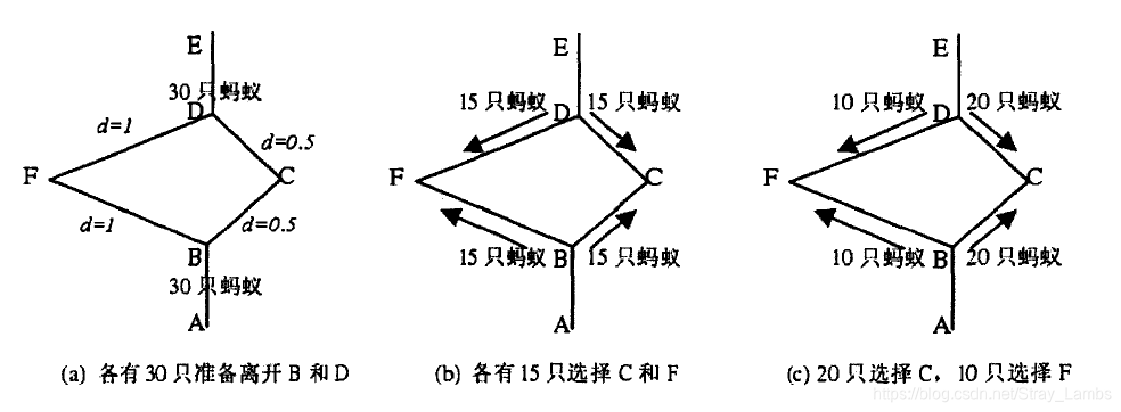
A为食物源;E为蚁穴;d为所需要的时间。
一开始在T=0的时刻,A和E同时出发了30只蚂蚁,由于路上都没有信息素的存在,15只蚂蚁走了BF,15只走了BC,15只蚂蚁走了DF,15只走了DC。在T=1的时刻,从A出发走BC->CD的蚂蚁已经到达了蚁穴,而另一边仅仅走到了一半,并且从E出发走DC->CB的蚂蚁也走到了食物源。在这个时刻BC和CD上的信息素就是另一边的两倍了(因为路径短蚂蚁已经到达终点)。在下一个时刻出发的蚂蚁则会根据信息素的浓度,来选择自身出发的方向。由于蚂蚁选择方向是依据信息素,但不完全依靠信息素。仅仅只会更倾向走向信息素浓度高的方向,但是依旧有可能走向浓度低的反向。所以第三幅图选择不同的方向的比重就不一样。
蚁群优化算法在优化过程中有两个重要的行为规则
1、蚂蚁对众多可行路径的选择规则:蚂蚁总是倾向于选择信息素浓度更高的路径。但这是概率的,信息素浓度低的路径也有被选择的可能。蚁群算法中的信息素类似于一种分布式的长期记忆,这种记忆不是局部地存储在于单个的人工蚂蚁上,而是全局地分布在整个问题空间里,是由整个蚁群共同协作形成的。信息素为蚁群中的蚂蚁提供了一种间接联络的方式。
2、全局信息素更新规则:在路径上的信息素,会随着时间的推移而逐步蒸发散失,路径上的信息素浓度会自然降低,这样没有被选择过的或较少被选择的路径上的信息素会越来越少,该路径会变得越来越不受蚂峡欢迎。每只蚂蚁可以按照路径的长短,或者是找到的食物的质量,在其经过的路径上留下相应数量的信息素。全局信息素更新规则的实质,是人工蚂蚁根据真实蚂蚁在访问过的路径上会留下信息素,以及信息素的自然蒸发过程,模拟出来的信息素更新机制,它会使得越好的解会得到越多的增强,越受蚂蚁的青睐。
蚁群算法内的参数设置:
m:蚂蚁数量,约为城市数量的1.5倍。如果蚂蚁数量过大,则每条路径上的信息素浓度趋于平均,正反馈作用减弱,从而导致收敛速度减慢;如果过小,则可能导致一些从未搜索过的路径信息素浓度减小为0,导致过早收敛,解的全局最优性降低;
α:信息素因子,反映了蚂蚁运动过程中积累的信息量在指导蚁群搜索中的相对重要程度,取值范围通常在[1, 4]之间。如果信息素因子值设置过大,则容易使随机搜索性减弱;其值过小容易过早陷入局部最优;
β:启发函数因子,反映了启发式信息在指导蚁群搜索中的相对重要程度,取值范围在[3, 4.5]之间。如果值设置过大,虽然收敛速度加快,但是易陷入局部最优;其值过小,蚁群易陷入纯粹的随机搜索,很难找到最优解;
ρ:信息素挥发因子,反映了信息素的消失水平,相反的反映了信息素的保持水平,取值范围通常在[0.2, 0.5]之间。当取值过大时,容易影响随机性和全局最优性;反之,收敛速度降低;
Q:信息素常数,表示蚂蚁遍历一次所有城市所释放的信息素总量。越大则收敛速度越快,但是容易陷入局部最优;反之会影响收敛速度。
我从网上博客找了段代码 (菜菜的我还是写不出来…
# -*- coding: utf-8 -*-
"""
Created on Wed Jun 16 15:21:03 2018
@author: SYSTEM
"""
import osos.getcwd()
#返回当前工作目录
import numpy as np
import matplotlib.pyplot as plt
# % pylab
#初始化城市坐标,总共52个城市
coordinates = np.array([[565.0, 575.0], [25.0, 185.0], [345.0, 750.0], [945.0, 685.0], [845.0, 655.0],[880.0, 660.0], [25.0, 230.0], [525.0, 1000.0], [580.0, 1175.0], [650.0, 1130.0],[1605.0, 620.0], [1220.0, 580.0], [1465.0, 200.0], [1530.0, 5.0], [845.0, 680.0],[725.0, 370.0], [145.0, 665.0], [415.0, 635.0], [510.0, 875.0], [560.0, 365.0],[300.0, 465.0], [520.0, 585.0], [480.0, 415.0], [835.0, 625.0], [975.0, 580.0],[1215.0, 245.0], [1320.0, 315.0], [1250.0, 400.0], [660.0, 180.0], [410.0, 250.0],[420.0, 555.0], [575.0, 665.0], [1150.0, 1160.0], [700.0, 580.0], [685.0, 595.0],[685.0, 610.0], [770.0, 610.0], [795.0, 645.0], [720.0, 635.0], [760.0, 650.0],[475.0, 960.0], [95.0, 260.0], [875.0, 920.0], [700.0, 500.0], [555.0, 815.0],[830.0, 485.0], [1170.0, 65.0], [830.0, 610.0], [605.0, 625.0], [595.0, 360.0],[1340.0, 725.0], [1740.0, 245.0]])#计算52个城市间的欧式距离
def getdistmat(coordinates):num = coordinates.shape[0]distmat = np.zeros((52, 52))# 初始化生成52*52的矩阵for i in range(num):for j in range(i, num):distmat[i][j] = distmat[j][i] = np.linalg.norm(coordinates[i] - coordinates[j])return distmat
#返回城市距离矩阵distmat = getdistmat(coordinates)numant = 60 # 蚂蚁个数
numcity = coordinates.shape[0]
# shape[0]=52 城市个数,也就是任务个数
alpha = 1 # 信息素重要程度因子
beta = 5 # 启发函数重要程度因子
rho = 0.1 # 信息素的挥发速度
Q = 1 # 完成率iter = 0 #迭代初始
itermax = 150 #迭代总数etatable = 1.0 / (distmat + np.diag([1e10] * numcity))
#diag(),将一维数组转化为方阵 启发函数矩阵,表示蚂蚁从城市i转移到城市j的期望程度
pheromonetable = np.ones((numcity, numcity))
# 信息素矩阵 52*52
pathtable = np.zeros((numant, numcity)).astype(int)
# 路径记录表,转化成整型 40*52
distmat = getdistmat(coordinates)
# 城市的距离矩阵 52*52lengthaver = np.zeros(itermax) # 迭代50次,存放每次迭代后,路径的平均长度 50*1
lengthbest = np.zeros(itermax) # 迭代50次,存放每次迭代后,最佳路径长度 50*1
pathbest = np.zeros((itermax, numcity)) # 迭代50次,存放每次迭代后,最佳路径城市的坐标 50*52while iter < itermax:#迭代总数#40个蚂蚁随机放置于52个城市中if numant <= numcity: # 城市数比蚂蚁数多,不用管pathtable[:, 0] = np.random.permutation(range(numcity))[:numant]#返回一个打乱的40*52矩阵,但是并不改变原来的数组,把这个数组的第一列(40个元素)放到路径表的第一列中#矩阵的意思是哪个蚂蚁在哪个城市,矩阵元素不大于52else: # 蚂蚁数比城市数多,需要有城市放多个蚂蚁pathtable[:numcity, 0] = np.random.permutation(range(numcity))[:]# 先放52个pathtable[numcity:, 0] = np.random.permutation(range(numcity))[:numant - numcity]# 再把剩下的放完# print(pathtable[:,0])length = np.zeros(numant) # 1*40的数组#本段程序算出每只/第i只蚂蚁转移到下一个城市的概率for i in range(numant):# i=0visiting = pathtable[i, 0] # 当前所在的城市# set()创建一个无序不重复元素集合# visited = set() #已访问过的城市,防止重复# visited.add(visiting) #增加元素unvisited = set(range(numcity))#未访问的城市集合#剔除重复的元素unvisited.remove(visiting) # 删除已经访问过的城市元素for j in range(1, numcity): # 循环numcity-1次,访问剩余的所有numcity-1个城市# j=1# 每次用轮盘法选择下一个要访问的城市listunvisited = list(unvisited)#未访问城市数,listprobtrans = np.zeros(len(listunvisited))#每次循环都初始化转移概率矩阵1*52,1*51,1*50,1*49....#以下是计算转移概率for k in range(len(listunvisited)):probtrans[k] = np.power(pheromonetable[visiting][listunvisited[k]], alpha) \* np.power(etatable[visiting][listunvisited[k]], alpha)#eta-从城市i到城市j的启发因子 这是概率公式的分母 其中[visiting][listunvis[k]]是从本城市到k城市的信息素cumsumprobtrans = (probtrans / sum(probtrans)).cumsum()#求出本只蚂蚁的转移到各个城市的概率斐波衲挈数列cumsumprobtrans -= np.random.rand()# 随机生成下个城市的转移概率,再用区间比较# k = listunvisited[find(cumsumprobtrans > 0)[0]]k = listunvisited[list(cumsumprobtrans > 0).index(True)]# k = listunvisited[np.where(cumsumprobtrans > 0)[0]]# where 函数选出符合cumsumprobtans>0的数# 下一个要访问的城市pathtable[i, j] = k#采用禁忌表来记录蚂蚁i当前走过的第j城市的坐标,这里走了第j个城市.k是中间值unvisited.remove(k)# visited.add(k)#将未访问城市列表中的K城市删去,增加到已访问城市列表中length[i] += distmat[visiting][k]#计算本城市到K城市的距离visiting = klength[i] += distmat[visiting][pathtable[i, 0]]# 计算本只蚂蚁的总的路径距离,包括最后一个城市和第一个城市的距离# print("ants all length:",length)# 包含所有蚂蚁的一个迭代结束后,统计本次迭代的若干统计参数lengthaver[iter] = length.mean()#本轮的平均路径#本部分是为了求出最佳路径if iter == 0:lengthbest[iter] = length.min()pathbest[iter] = pathtable[length.argmin()].copy()#如果是第一轮路径,则选择本轮最短的路径,并返回索引值下标,并将其记录else:#后面几轮的情况,更新最佳路径if length.min() > lengthbest[iter - 1]:lengthbest[iter] = lengthbest[iter - 1]pathbest[iter] = pathbest[iter - 1].copy()# 如果是第一轮路径,则选择本轮最短的路径,并返回索引值下标,并将其记录else:lengthbest[iter] = length.min()pathbest[iter] = pathtable[length.argmin()].copy()#此部分是为了更新信息素changepheromonetable = np.zeros((numcity, numcity))for i in range(numant):#更新所有的蚂蚁for j in range(numcity - 1):changepheromonetable[pathtable[i, j]][pathtable[i, j + 1]] += Q / distmat[pathtable[i, j]][pathtable[i, j + 1]]#根据公式更新本只蚂蚁改变的城市间的信息素 Q/d 其中d是从第j个城市到第j+1个城市的距离changepheromonetable[pathtable[i, j + 1]][pathtable[i, 0]] += Q / distmat[pathtable[i, j + 1]][pathtable[i, 0]]#首城市到最后一个城市 所有蚂蚁改变的信息素总和#信息素更新公式p=(1-挥发速率)*现有信息素+改变的信息素pheromonetable = (1 - rho) * pheromonetable + changepheromonetableiter += 1 # 迭代次数指示器+1print("this iteration end:",iter)# 观察程序执行进度,该功能是非必须的if (iter - 1) % 20 == 0:print("schedule:",iter - 1)
#迭代完成#以下是做图部分
#做出平均路径长度和最优路径长度
fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(12, 10))
axes[0].plot(lengthaver, 'k', marker='*')
axes[0].set_title('Average Length')
axes[0].set_xlabel(u'iteration')#线条颜色black https://blog.csdn.net/ywjun0919/article/details/8692018
axes[1].plot(lengthbest, 'k', marker='<')
axes[1].set_title('Best Length')
axes[1].set_xlabel(u'iteration')
fig.savefig('Average_Best.png', dpi=500, bbox_inches='tight')
plt.close()
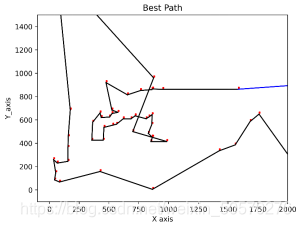
fig.show()# 作出找到的最优路径图
bestpath = pathbest[-1]plt.plot(coordinates[:, 0], coordinates[:, 1], 'r.', marker='>')
plt.xlim([-100, 2000])
#x范围
plt.ylim([-100, 1500])
#y范围for i in range(numcity - 1):#按坐标绘出最佳两两城市间路径m, n = int(bestpath[i]), int(bestpath[i + 1])print("best_path:",m, n)plt.plot([coordinates[m][0],coordinates[n][0]], [coordinates[m][1], coordinates[n][1]], 'k')plt.plot([coordinates[int(bestpath[0])][0],coordinates[int(bestpath[51])][0]], [coordinates[int(bestpath[0])][1],coordinates[int(bestpath[50])][1]] ,'b')ax = plt.gca()
ax.set_title("Best Path")
ax.set_xlabel('X_axis')
ax.set_ylabel('Y_axis')plt.savefig('Best Path.png', dpi=500, bbox_inches='tight')
plt.close()
# 代码来自https://blog.csdn.net/quinn1994/article/details/80324308
记录一下,共勉。