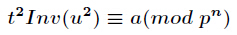Deep Upsupervised Cardinality Estimation 解读(2019 VLDB)
- Deep Upsupervised Cardinality Estimation
- 选择度(基数)估计问题定义
- 选择度和数据联合分布的关系
- 深度自回归模型如何计算joint distribution
- 编码解码策略
- 具体执行
- 属性的顺序
- 均匀采样和渐进采样
Deep Upsupervised Cardinality Estimation
- 本篇博客是对Deep Upsupervised Cardinality Estimation的解读,原文连接为:https://dl.acm.org/doi/pdf/10.14778/3368289.3368294
- 本文介绍了如何使用深度自回归模型(如:MADE、transformer)来进行基数估计的任务(利用模型训练拟合数据分布)
- 特点:
- 使用autoregressive model,无监督学习
- 没有做任何独立性假设
- 支持范围查询
选择度(基数)估计问题定义
- selectivity——选择度。本文针对的是给定谓词,估计其可以估计数据表中满足该谓词的元组的比例,有如下定义: s e l ( θ ) : = ∣ { x ∈ T : θ ( x ) = 1 } ∣ / ∣ T ∣ sel(\theta):=|\{\ x \in T :\theta (x)=1\}|/|T| sel(θ):=∣{ x∈T:θ(x)=1}∣/∣T∣
其中分母T就是表的总行数,分子是满足选择谓词的行数。
选择度和数据联合分布的关系
- 文中给出联合分布(joint distribution)的定义:
P ( a 1 , a 2 , . . . , a n ) : = f ( a 1 , a 2 , . . . , a n ) / T P(a_1,a_2,...,a_n):=f(a_1,a_2,...,a_n)/T P(a1,a2,...,an):=f(a1,a2,...,an)/T
其中分母T仍表示表行数,f为满足a1,a2…an条件的行数。因此实际上联合分布和选择度有着十分紧密的联系(基本一致)。同时联合分布还可以通过因式分解(factorization)写成:
P ( A 1 , A 2 , . . . A n ) : = P ^ ( A 1 ) P ^ ( A 2 ∣ A 1 ) . . . P ^ ( A n ∣ A 1 , A 2 , . . . A n − 1 ) P(A_1,A_2,...A_n):=\hat{P}(A_1) \hat{P}(A_2|A_1)...\hat{P}(A_n|A_1,A_2,...A_{n-1}) P(A1,A2,...An):=P^(A1)P^(A2∣A1)...P^(An∣A1,A2,...An−1)
该式没有进行任何独立性假设,而且保留了属性之间的相互联系,因此想获得相对准确的选择度,实际上就是要构建能计算上式的模型。
深度自回归模型如何计算joint distribution
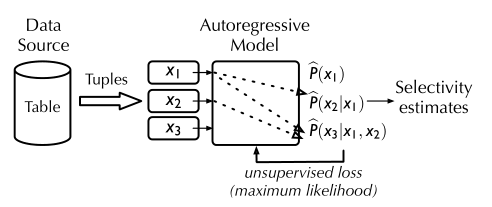
- 作者选用Autoregressive Model进行对数据联合分布的拟合。以某一列为例。对于一列数据的分布,模型的input为前几列值的组合(因为是条件概率),输出的是在前几列的条件下,改列的分布概率。例如一张表travel_checkins含有三个属性:city、year、stars。给定一行作为输入:<Portland;2017;10>:
- 0 → M ( c i t y ) 0\rightarrow M(city) 0→M(city)
E c i t y ( P o r t l a n d ) → M ( y e a r ) E_{city}(Portland)\rightarrow M(year) Ecity(Portland)→M(year)
( E c i t y ( P o r t l a n d ) ⊕ E y e a r ( 2017 ) ) → M s t a r (E_{city}(Portland)\oplus E_{year}(2017)) \rightarrow M_{star} (Ecity(Portland)⊕Eyear(2017))→Mstar
上式三个输出依次是条件概率: P ^ ( c i t y ) , P ^ ( y e a r ∣ c i t y ) , P ^ ( s t a r ∣ c i t y , y e a r ) \hat{P}(city),\hat{P}(year|city),\hat{P}(star|city,year) P^(city),P^(year∣city),P^(star∣city,year)
- 下图简略展示了模型的工作流
编码解码策略
在训练模型时,我们必须将数据表中的各个元素编码成机器能够看懂的语言,模型输出时我们要将编码进行解码得到各种概率,下面介绍作者提出的编码解码策略。
-
small-domain:
- encodding:one-hot
- decoding:一个全连接层FC(F,|Ai|),其中F为隐藏层大小,|Ai|第i列的值域大小。输出一个长度|Ai|的向量,每个元素表示位于该值的概率。
-
large-domain:
- encodding:Embedding,通过词嵌入将各值映射为一个固定长度h的向量
- decoding:Embedding reuse。当属性值域太大时,向上面一样使用一个全连接层产生一个非常长的向量,这在空间上和计算复杂度上都十分低效。在这里作者提出Embedding reuse,同样使用一个全连接层FC(F,h),其中F还是隐藏层的大小,h为Embedding规定的向量长度,这样神经网络就会生成一个长度为h的向量H,接着通过计算 H E i T HE_i^T HEiT并对其进行标准化处理,我们就能得到一个代表选择度的度量值。
具体执行
本文提供的方法支持点查询和范围查询,一般来说 s e l = P ( X 1 ∈ R 1 , X 2 ∈ R 2 , . . . X n ∈ R 3 ) sel=P(X_1\in R_1,X_2\in R_2,...X_n\in R_3) sel=P(X1∈R1,X2∈R2,...Xn∈R3)
- 点查询,即等值查询,将上式转换为: s e l = P ( X 1 = x 1 , X 2 = x 2 , . . . X n = x 3 ) sel=P(X_1=x_1,X_2=x_2,...X_n=x_3) sel=P(X1=x1,X2=x2,...Xn=x3)
- 范围查询:对于范围查询,本文采用渐进采样的方法对数据表进行采样进行概率的估计
- wildcard-skipping:这里提到的通配符不是指like查询,而是指age = any,也就是age可以为任何值,即范围查询age = [0, Di]。所以这里提到的通配符是为了满足有些条件没有filter的处理。
为了达到这个目的,作者设计了特殊的token,Xi = MASKi,如age这一列的token为MASK_age。训练的时候,会把每一列用这个token替换掉,进行训练(这样就需要训练n次?n为列的个数,相当于数据被复制了n份,每一份把一列的值替换为token)。
实际操作的时候,会随机sample一个tuple,age对应的值换成MASK_age,表明age取所有值,其他值的条件概率就是当age取所有值的情况下,其条件概率为多少,作为label。至于sample多少条数据,这个要看具体效果了。
另外要根据实际的query确定哪些列需要有这个通配符。再举个具体的例子,一个表有三列a b c,查询为a=1,那么模型训练的时候必须要有b=MASK_b,c=MASK_c,查询的输入为a=1, b=MASK_b,c=MASK_c。再如a<10,一种方法是sampling,还有一种方法是模型训练的时候要有a=MASK_a, 这样查询的时候输入是a=MASK_a, b=MASK_b,c=MASK_c,a的输出会得到所有的值,再把<10对应的值的概率加起来。
所以,这个通配符是非常有用的,因为在真实查询中,不可能保证所有列上都有条件,那么没有条件的列就用通配符替代。当然也可以用sampling的方式,但是通配符的查询效率更高。
属性的顺序
从上面的分析中可以看到每列实际上是有顺序的,比如模型的输入是列a b c,输出是条件概率,既然是条件概率,那么b的概率是给定a得到,c的概率是给定a和b得到。所以这个顺序要提前定好,如果查询是b=1 a=2,需要把顺序调整成a=2 b=1输入到模型。
均匀采样和渐进采样
两种sampling策略是为了解决范围查询的选择度估计问题。
假定一个范围查询域 R = R 1 × R 2 × . . . × R n R=R_1\times R_2 \times ... \times R_n R=R1×R2×...×Rn,如果用等值的方法处理这种问题,在某种比较坏的情况下,查询域可能会非常大(比如可能为 ∣ A 1 ∣ × ∣ A 2 ∣ . . . ∣ A n ∣ |A_1|\times |A_2| ... |A_n| ∣A1∣×∣A2∣...∣An∣),此时非常耗费时间和空间。为了解决这种问题,本文尝试了两种解决方案:
-
uniformly sampling
- 从R(查询域)中均匀随机抽样出 x ( i ) x^{(i)} x(i),接着将该 x ( i ) x^{(i)} x(i)输入模型,计算出该样本在数据表中的概率: p i ^ = P ^ ( x ( i ) ) \hat{p_i}=\hat{P}(x^{(i)}) pi^=P^(x(i)),基于朴素蒙特卡洛,对于S个样本,我们可以将 ∣ R ∣ S ∑ i = 1 S p i ^ \frac{|R|}{S}\sum_{i=1}^{S}\hat{p_i} S∣R∣∑i=1Spi^作为期望密度的无偏估计。简单来说,该方案是将点随机扔到目标区域R中,以探测其平均密度。
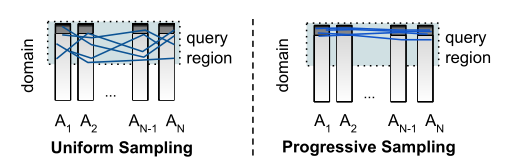
- 均匀采样的缺点:考虑这样一个情况,数据表T有n个属性列,但每一列的数据都非常倾斜,有99%的数据只集中在前1%的值域中,剩下1%的数据分散到后99%的值域内。在这种情况下,如果我们想进行值域前50%的范围查询。通过随机抽样我们大概率只能抽到1%-50%内的数据,计算出的结果会严重失真。如果要保持准确性,我们必须抽 1 / ( 0.01 / 0.5 ) n = 1 / 0.0 2 n 1/(0.01/0.5)^n=1/0.02^n 1/(0.01/0.5)n=1/0.02n个样本才能都取到数据高密度区域。真实的数据集中,这样倾斜的数据常有出现,当均匀抽样遇到这样的数据会很快崩溃,产生非常大的误差如下图左,这里我们使用下文提出的渐进采样来决绝该问题。
-
progressive sampling
- 渐进采样。在均匀采样中,我们是随机的在查询域中选择了一组样本。但实际上,我们可以更有选择性的挑选样本。具体来说我们可以利用模型一边生成各个属性的概率分布,一边按照生成的概率分布进行采样,因为是逐步进行采样的所以叫渐进采样。通过渐进采样,我们能很容易的采样到高数据密度的区域,如上图右。步骤如下:
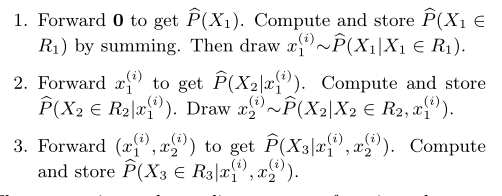
- 渐进采样。在均匀采样中,我们是随机的在查询域中选择了一组样本。但实际上,我们可以更有选择性的挑选样本。具体来说我们可以利用模型一边生成各个属性的概率分布,一边按照生成的概率分布进行采样,因为是逐步进行采样的所以叫渐进采样。通过渐进采样,我们能很容易的采样到高数据密度的区域,如上图右。步骤如下:
(*^▽^*)
(*^▽^*)
(*^▽^*)
(*^▽^*)
(*^▽^*)
笔者解读不易,若是有所帮助,给笔者点个赞吧(*^▽^*)
欢迎来与笔者交流相关问题!