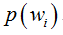函数声明：void *memcpy(void*dest, const void *src, size_t n);//n代表的是字节

使用方法：由src指向地址为起始地址的连续n个字节的数据复制到以dest指向地址为起始地址的空间内。

返回值：在未开始复制之前，dest指向的地址。

说明：1.src和dest所指内存区域不能重叠。

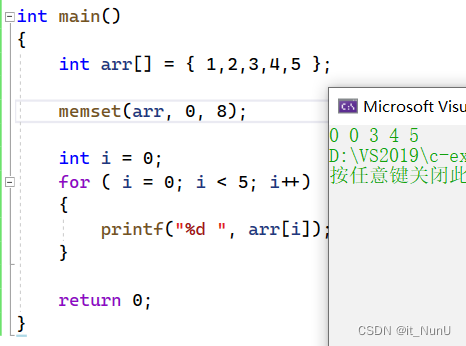
　　    2.与strcpy相比，memcpy并不是遇到'\0'就结束，而是一定会拷贝完n个字节。

           3.memcpy用来做内存拷贝，你可以拿它拷贝任何数据类型的对象，可以指定拷贝的数据长度。

举例子：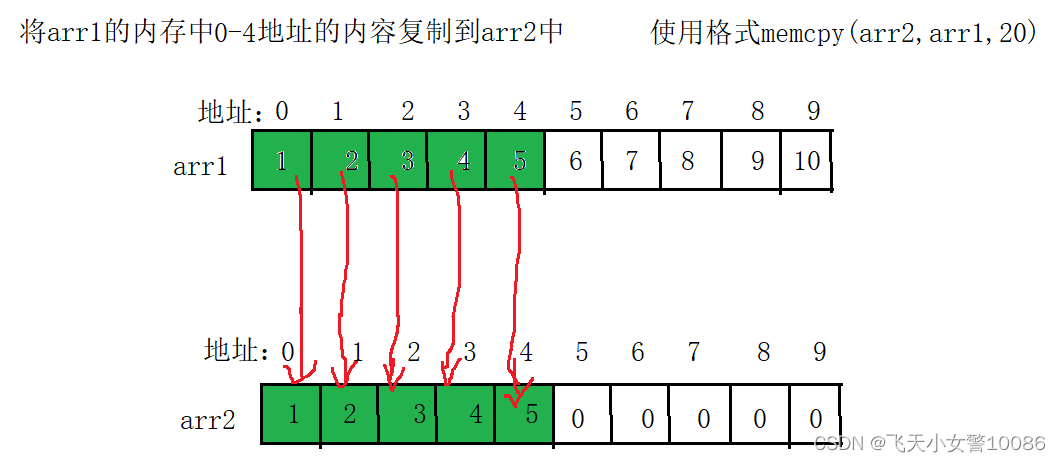

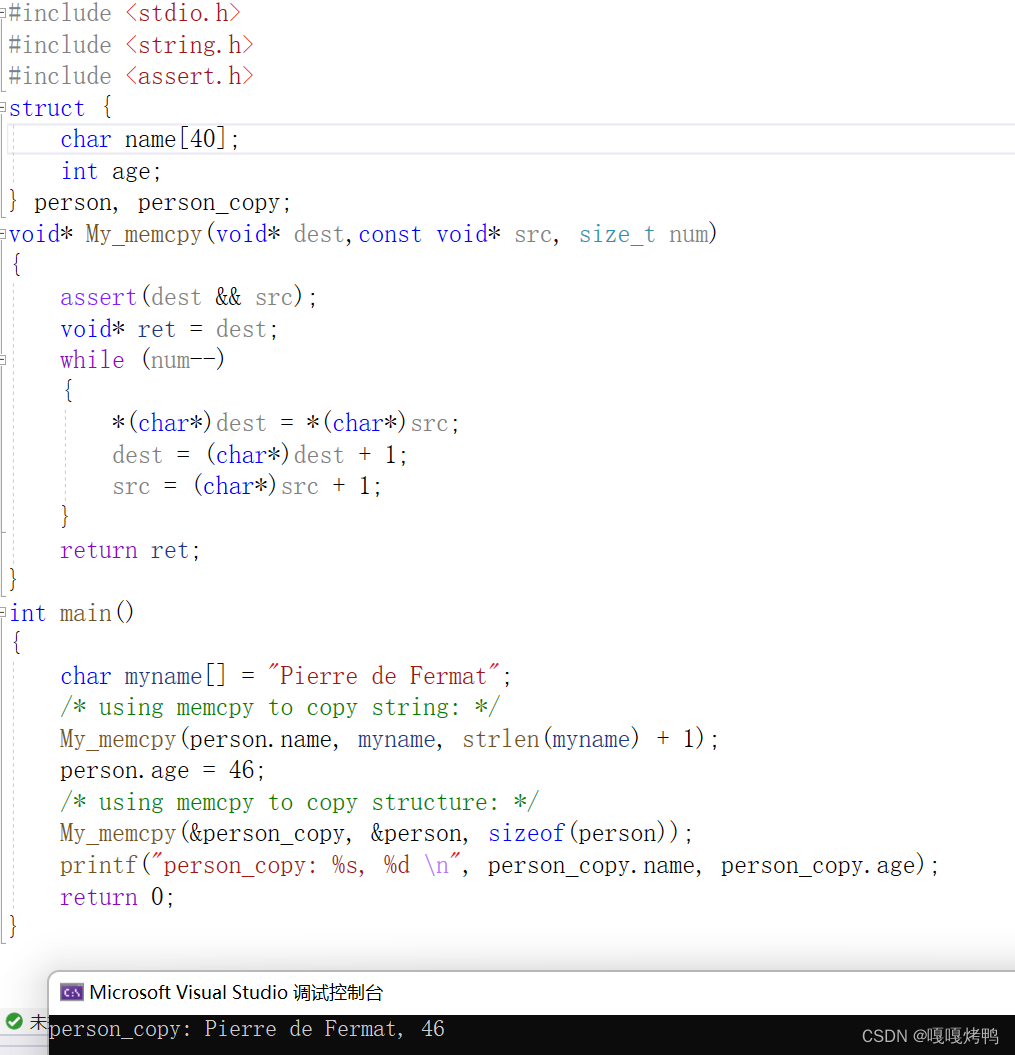
 简单实现memcpy函数：

#include<stdio.h>
#include<assert.h>
void* my_memcpy(void*dest,void*src,size_t num )
{
    void* p = dest;
    assert(dest);//对指针进行断言，不能为空指针 
    assert(src);
    while (num--)
    {
        *(char*)dest = *(char*)src;
        dest = (char*)dest + 1;
        src = (char*)src + 1; 
    }
    return p;
    
}

int main()
{
    int arr1[] = {1,2,3,4，5,6,7,8,9,10};
    int arr2[10] = { 0 };

    my_memcpy(arr2,arr1,20);
    for (int i = 0; i < 10; i++)
    {
        printf("%d ", arr2[i]);
    }
    return 0;
}