数学分析多元函数微分学(第17章)

article/2025/11/6 12:16:19

一.可微性
1.可微性与全微分:
在这里插入图片描述
2.偏导数:

3.可微性条件

对一元函数,可微和可导是等价的;但对多元函数,即使偏导数都存在,该函数也不一定可微

(1)可微的必要条件:

定理17.1:若二元函数 $f$ 在其定义域内1点 $x_0,y_0)$ 处可微,则 $f$ 在该点处关于每个自变量的偏导数都存在,且(1)式中的 $A=f_x(x_0,y_0),B=f_y(x_0,y_0)$ 因此,函数 $f$ 在点 $x_0,y_0)$ 处的全微分(2)可唯一地表示为 $df\,|_{(x_0,y_0)}=f_x(x_0,y_0)·Δx+f_y(x_0,y_0)·Δy$ 与一元函数的情况相同,由于自变量的增量等于自变量的微分,即 $Δ x = d x, Δ y = d y$ 故 $f$ 在点 $x_0,y_0)$ 处的全微分又可写为 $dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy$
若函数 $f$ 在区域 $D$ 上每1点 $(x, y)$ 都可微,则称函数 $f$ 在区域 $D$ 上可微,且 $f$ 在 $D$ 上的全微分为 $df(x,y)=f_x(x,y)dx+f_y(x,y)dy\qquad(8)$

(2)可微的充分条件:

定理17.2:若函数 $z = f (x, y)$ 的偏导数在点 $x_0,y_0)$ 的某邻域内存在,且 $f_x$ 与 $f_y$ 在点 $x_0,y_0)$ 处连续,则函数 $f$ 在点 $x_0,y_0)$ 处可微

(3)中值公式:

定理17.2证明过程中出现的(9)式,是二元函数的1个中值公式,可概括为下述定理:
定理17.3:设函数 $f$ 在点 $x_0,y_0)$ 的某邻域内存在偏导数,若 $(x, y)$ 属于该邻域,则 $∃\xi=x_0+θ_1(x-x_0)$ 和 $η=y_0+θ_2(y-y_0)\,(0<θ_1,θ_2<1)$ ,使得 $f(x,y)-f(x_0,y_0)=f_x(\xi,y)(x-x_0)+f_y(x_0,η)(y-y_0)\qquad(12)$

4.可微性的几何意义及应用
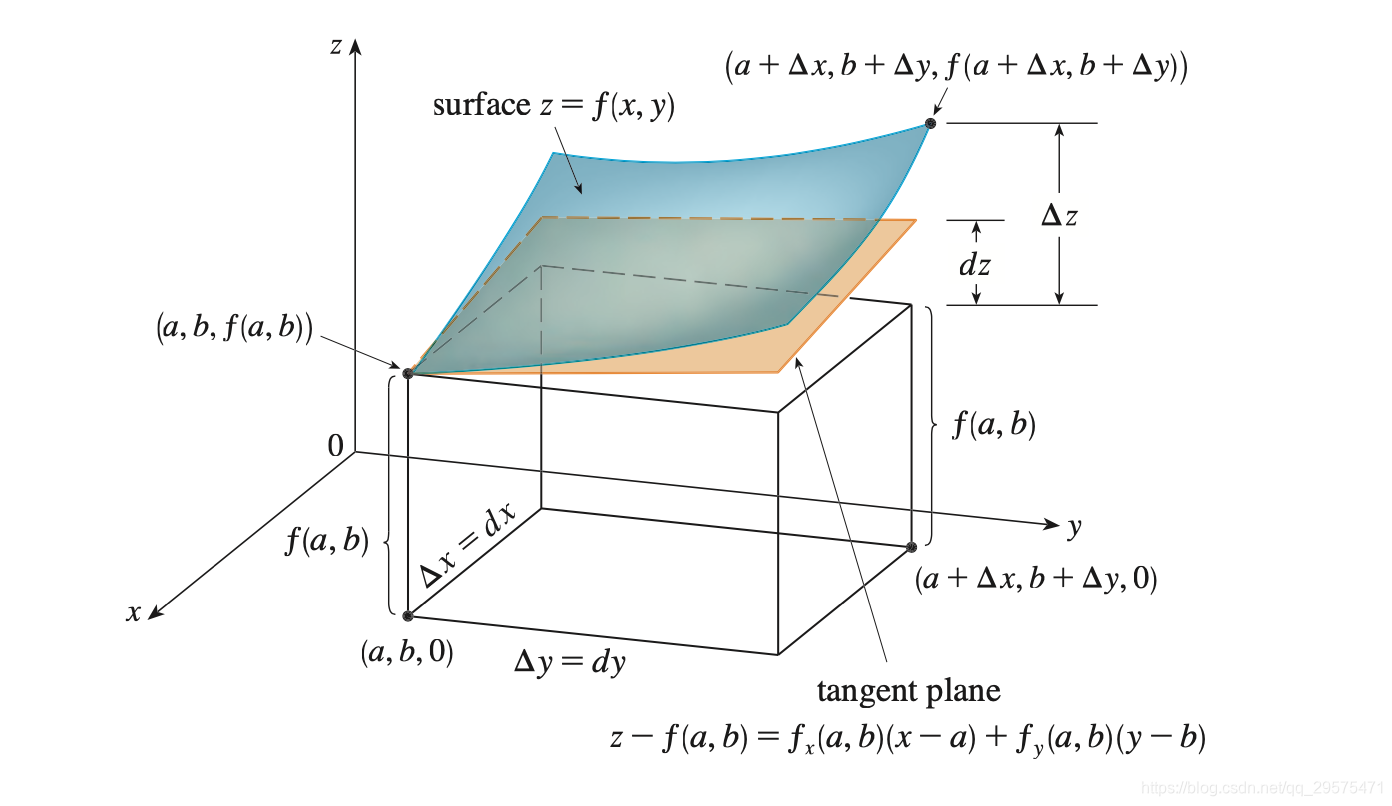
(1)切平面:
在这里插入图片描述
(2)切平面的存在性:

定理17.4:曲面 $z = f (x, y)$ 在点 $P(x_0,y_0,f(x_0,y_0))$ 处存在不平行于 $z$ 轴的切平面 $Π$ 的充要条件是:函数 $f$ 在点 $P_0(x_0,y_0)$ 处可微

(3)法线:
在这里插入图片描述
(4)全微分的几何意义:

二.复合函数微分法
1.复合函数求导法则
(1)复合函数:

(2)链式法则:

定理17.5:若函数 $x = φ (s, t), y = ψ (s, t)$ 在点 $(s, t) \in D$ 处可微,函数 $z = f (x, y)$ 在点 $(x, y) = (φ (s, t), ψ (s, t))$ 处可微,则复合函数 $z = f (φ (s, t), ψ (s, t))$ 在点 $(s, t)$ 处可微,且它关于 $s, t$ 的偏导数分别为: $\begin{matrix}\frac{\partial z}{\partial s}|_{(s,t)}=\frac{\partial z}{\partial x}|_{(x,y)}\frac{\partial x}{\partial s}|_{(s,t)}+\frac{\partial z}{\partial y}|_{(x,y)}\frac{\partial y}{\partial s}|_{(s,t)}\\\frac{\partial z}{\partial t}|_{(s,t)}=\frac{\partial z}{\partial x}|_{(x,y)}\frac{\partial x}{\partial t}|_{(s,t)}+\frac{\partial z}{\partial y}|_{(x,y)}\frac{\partial y}{\partial t}|_{(s,t)}\end{matrix}\qquad(4)$

注意事项:

2.复合函数的全微分:
在这里插入图片描述
三.方向导数与梯度
1.方向导数:

2.方向导数与偏导数的关系:

定理17.6:若函数 $f$ 在点 $P_0(x_0,y_0,z_0)$ 处可微,则 $f$ 在点 $P_0$ 处沿任一方向 $l$ 的方向导数都存在,且 $f_l(P_0)=f_x(P_0)cosα+f_y(P_0)cosβ+f_z(P_0)cosγ\qquad(1)$ 其中 $c o s α, c o s β, c o s γ$ 为方向 $l$ 的方向余弦

3.方向导数的存在性:
在这里插入图片描述

4.梯度:

四.泰勒公式与极限问题
1.高阶偏导数
(1)定义:

(2)混合偏导数相等(累次极限次序可交换)的条件:

定理17.7:若 $f_{xy}(x_0,y_0),f_{yx}(x_0,y_0)$ 都在点 $x_0,y_0)$ 处连续,则 $f_{xy}(x_0,y_0)=f_{yx}(x_0,y_0)\qquad(3)$

(3)复合函数的高阶偏导数:
在这里插入图片描述

2.中值定理与泰勒公式
(1)凸区域:

(2)中值定理:

定理17.8:设二元函数 $f$ 在凸区域 $D\sub R^2$ 上可微,则对 $\forall 2$ 点 $P(a,b),Q(a+h,b+k)∈D,∃θ∈R\,(0<θ<1)$ ,使得 $f(a+h,b+k)-f(a,b)\qquad\qquad\qquad\qquad\quad\\=f_x(a+θh,b+θk)h+f_y(a+θh,b+θk)k\qquad(8)$

注意:若 $P, Q$ 为矩形闭域 $D$ 边界上的点,这些点不是内点 $(\notin int D)$ ,这些点处不能全微分,即不可微,故定理不成立

推论:若函数 $f$ 在区域 $D$ 上存在偏导数,且 $f_x=f_y\equiv0$ 则 $f$ 在 $D$ 上为常量函数

(3)泰勒定理:

定理17.9:若函数 $f$ 在点 $P_0(x_0,y_0)$ 的某邻域 $U(P_0)$ 上有直到 $n + 1$ 阶的连续偏导数,则对 $U(P_0)$ 上任1点 $x_0+h,y_0+k),∃$ 相应的 $θ \in (0, 1)$ ,使得 $f(x_0+h,y_0+k)=f(x_0,y_0)\\\qquad\qquad\qquad\qquad\qquad\qquad\quad\:+(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y})f(x_0,y_0)\\\qquad\qquad\qquad\qquad\qquad\qquad\quad\:+\frac{1}{2!}(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y})^2f(x_0,y_0)\\\qquad\qquad\qquad\:\:\,+...\\\qquad\qquad\qquad\qquad\qquad\qquad\quad\:+\frac{1}{n!}(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y})^nf(x_0,y_0)\\\qquad\qquad\qquad\qquad\qquad\qquad\quad\:+\frac{1}{(n+1)!}(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y})^{n+1}f(x_0+θh,y_0+θk)\\\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\:\:\:(11)$ (11)式称为二元函数 $f$ 在点 $P_0$ 处的 $n$ 阶泰勒公式,其中 $(h\frac{\partial}{\partial x}+k\frac{\partial}{\partial y})^mf(x_0,y_0)=\displaystyle\sum_{i=0}^mC^i_m\frac{\partial^m}{\partial x^iy^{m-i}}h^ik^{m-i}$

3.极值问题
(1)极值与极值点:
在这里插入图片描述
(2)极值必要条件:

定理17.10:若函数 $f$ 在点 $P_0(x_0,y_0)$ 处存在偏导数,且在 $P_0$ 取得极值,则有 $f_x(x_0,y_0)=f_y(x_0,y_0)=0\qquad(16)$

(3)海塞矩阵(Hesse Matrix)与极值充分条件:
在这里插入图片描述

注:①海塞矩阵的一般形式见第23章

定理17.11:设二元函数 $f$ 在点 $P_0(x_0,y_0)$ 的某邻域 $U(P_0)$ 上具有二阶连续偏导数,且 $P_0$ 是 $f$ 的稳定点,则当 $H_f(P_0)$ 是正定矩阵时, $f$ 在 $P_0$ 取得极小值;当 $H_f(P_0)$ 是负定矩阵时, $f$ 在点 $P_0$ 取得极大值;当 $H_f(P_0)$ 是不定矩阵时, $f$ 在 $P_0$ 不取极值