看几个知乎大佬的解释之后,有些头绪了。梳理一下自己的理解。
1、微分是个什么东西?
先从一元微分下手:
一元微分是什么?
结论:两个身份:线性变化量,是函数变化的逼近
从公式可以看出:
线性变化量:dy=AΔx
函数变化的逼近: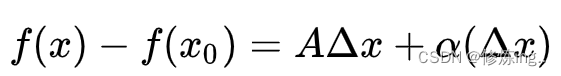

引入微分的作用?它能干啥?
从两个角度出发来理解:
1、研究函数在某点的变化情况
古典微分(还没有提出极限):设想知道x0邻域变化情况,用一个x1去接近它,可以求出fx1-fx0的差值,即Δf。
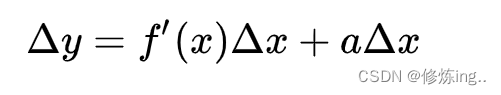
当无限接近的时候,认为Δx=0,推出dy=Δy,dy称y的微分。为了研究变化情况,引入切线斜率(如果知道它斜率就可以知道变化情况),Δy/Δx=dy/dx=A(当年的导数还没有极限)。这其实很矛盾,前面认为Δx等于0了,后面又拿它来当分母。。。
引入极限的思想:
极限微分学(也就是我们学的):用极限来表示这个“无限接近”。
从导数下手:
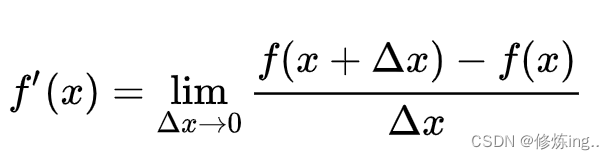
引入极限后,切线斜率就可以用割线斜率的极限来表示了。lim Δy/Δx=A。求斜率问题解决。
再回到微分定义公式:dy=AΔx
当Δx趋向0,dy不断逼近Δy。可以看出,微分是一种逼近,对变化量的逼近。
2、以直代曲(我感觉从这个角度更好理解)
问题提出:
由于大部分的函数并不是线性的,要求它某一点的函数值是很有难度的。能不能在某点的邻域内,用一个线性函数来表示该函数的邻域呢?如果可以,该点附近函数值和变化趋势不就都好求了吗?(以直代曲)
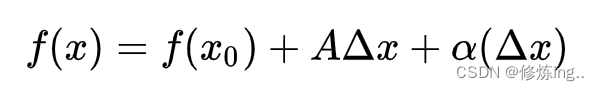
x是指在x0附件取点。即fx可以由一个线性函数+误差表示出来(即左右等价)—其实发现这也是可微的定义。
如果能求出误差,不就能将邻域情况表示出来了吗?
问题是求不出来。
换一个思路,让误差尽量小,小到什么程度—看你需要的精度呗,即设定某个接收阈值,误差小于这个阈值可以认为以直代曲成功。
引入极限的思想,认为如果误差与线性部分的比值(Δx是取趋于0极限的)=0,则认为这个误差是无足轻重的。
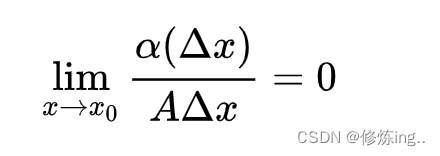
由此:可微:在某点的邻域内,可以以直代曲,这种做法是可接受的(误差无足轻重)
误差已经解决了,接下来找A
A即线性部分的斜率。
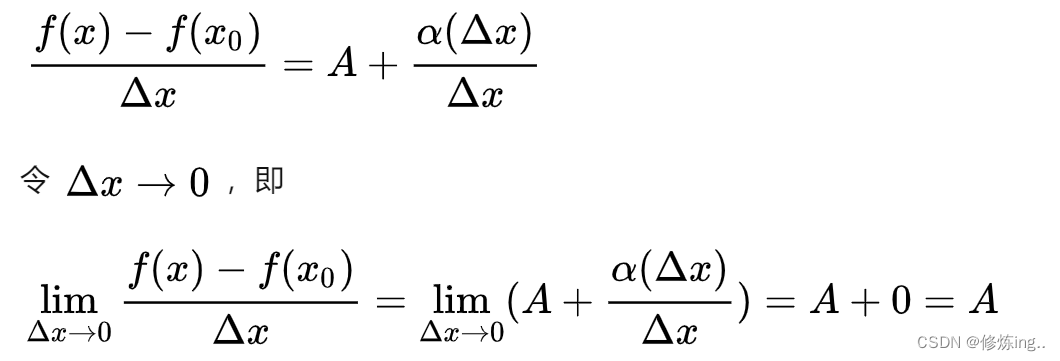
最左边的那个极限我们称为导数。求A即求导数就好了,不用知道fx是多少,通过求极限的方法来求导数。
由此:以直代曲成功!
再回到微分定义公式:dy=AΔx ,以直代曲中线性的主体部分
导数–斜率,取微分–以直代曲这个操作本身
1、全微分、偏导数、连续
一元:以直(切线)代曲
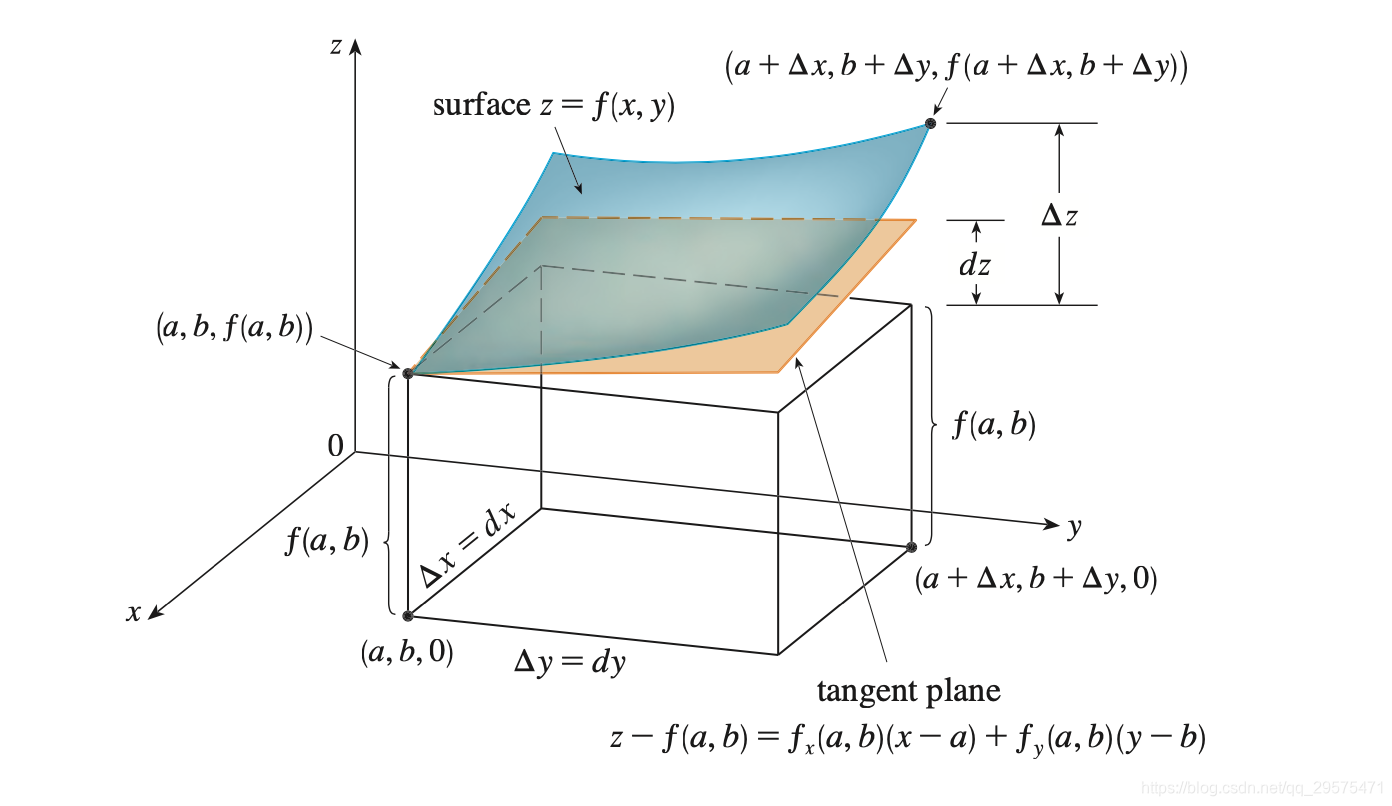
二元:以面(切平面)代曲
类比一元,想求出z在某点邻域情况。如果能用一个平面来表示该邻域情况,那变化情况就好求了。
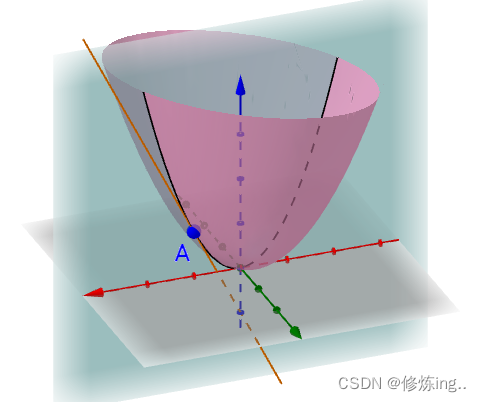
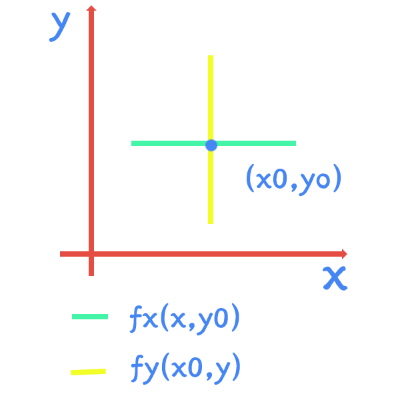
平行z轴做平面,与曲面某点相交-得到相交曲线,对于该曲线(回到一元理解了)可做切线,如果此时x=C,即曲线在yz平面中,切线斜率即所谓对y偏导数。
全微分:类比一元:
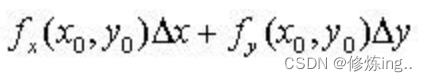
这里主要想讨论连续、偏导、全微的关系。
全微即:找得到一个切平面来表示某点邻域,即无数个平行z轴且过该点的平面与曲面相交,得到无数曲线,这些曲线的切线都存在,即360°微分都存在–可全微。
可偏导–x/y轴方向可微罢了,很明显是全微必要条件。
不连续,连切线找不到,更别谈全微了
偏导数存在能推出连续吗?
只能说在某个方向它是连续的,但其他方向不一定。多元函数连续,说的是所有方向都连续。
连续能推出偏导数存在吗?
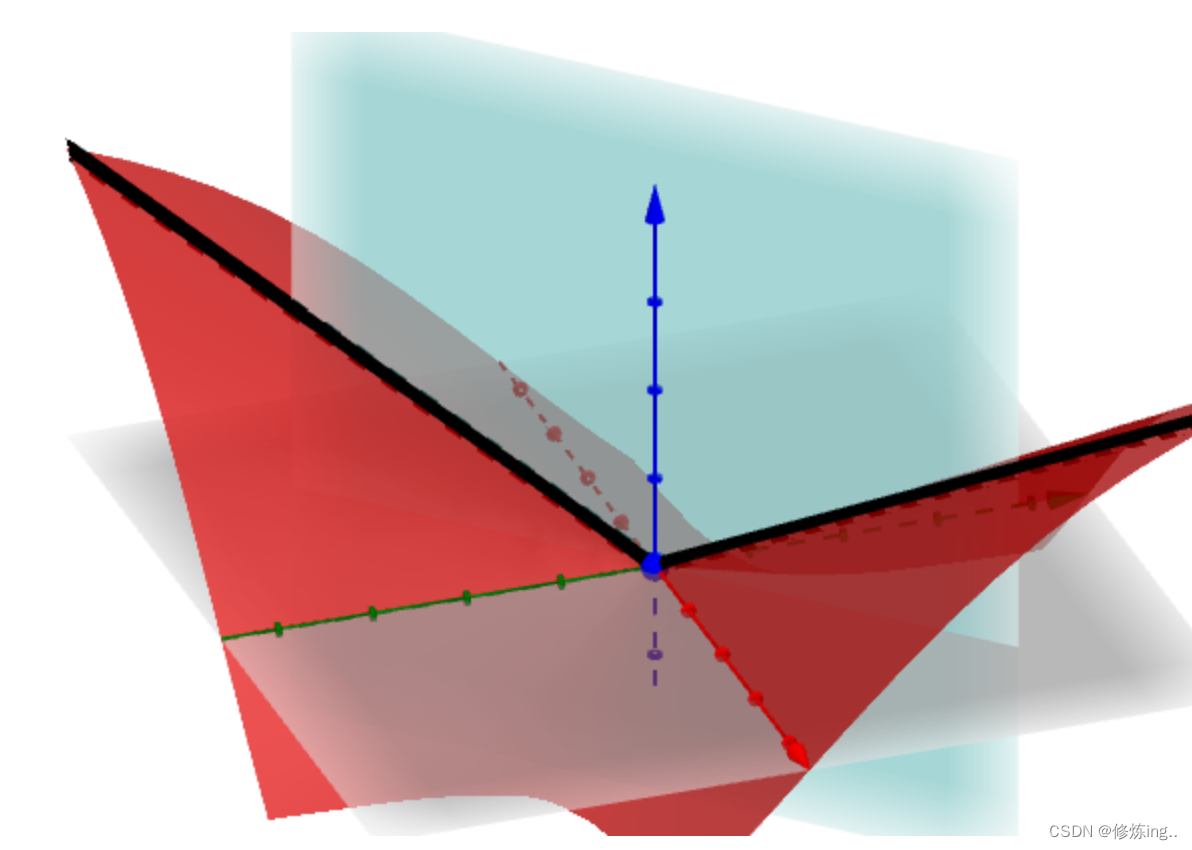](https://img-blog.csdnimg.cn/da7b29f57e7b413e9c83dfb981f9ca86.png)
很明显,此时该曲线有尖点,偏导数不存在。
微分这里思考了很久也不敢写总结,还是理解的不够,先力所能及地写,后面再改!
参考了许多大佬地文章:这里先贴一下链接,方便以后查找:
多元函数中可微与可导的直观区别是什么? --马同学
如何通俗理解全微分 --刘梳子
微分、导数、积分,这三者之间,有没有联系? --湖心亭看雪
导数与微分到底有什么区别? --了不起地盖茨比