多元函数-连续 偏导 可微

定义

1.连续定义

设二元函数$f(P)=f(x,y)$的定义域为D, $P_0(x_0,y_0)$为D的聚点，且$P_0\in D$,若

$$li{m}_{(x,y)\to (x_0,y_0)}f(x,y)=f(x_0,y_0)$$

则称函数$f(x,y)$在$P_0$连续

聚点：如果给定任意的$\delta >0$，点P的去心领域$U(P,\delta )$内总有E的点，那么称P是E的聚点

2.偏导定义

设函数$z=f(x,y)$在点$(x_0,y_0)$的某一领域内有定义，当$y$固定在$y_0$，而x在$x_0$处有增量$\Delta x$时，相应的函数有增量

$$f(x_0+\Delta x,y_0)-f(x_0,y_0)$$

如果

$$li{m}_{\Delta x\to 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}$$

存在，那么称此极限为函数$z=f(x,y)$在点$(x_0,y_0)$处对$x$的偏导数，记作

$\frac{\partial z}{\partial x}{|}_{x=x_0,y=y_0}$ , $\frac{\partial f}{\partial x}{|}_{x=x_0,y=y_0}$,$\frac{Z_x}{\partial x}{|}_{x=x_0,y=y_0}$ 或 $f_x(x_0,y_0)$

3.可微定义

设函数$z=f(x,y)$在点$(x,y)$的某领域内有定义，如果函数在$(x,y)$的全增量

$$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$$

可表示为

$$\Delta z=A\Delta x+B\Delta y+o(\rho )$$

其中A和B不依赖于$\Delta x$ 和 $\Delta y$而仅与x和y有关，$\rho =\sqrt{(\Delta x{)}^2+\Delta y{)}^2}$，那么称函数$z=f(x,y)$在点$(x,y)$可微分，而$A\Delta x+B\Delta y$称为函数$z=f(x,y)$在点$(x,y)$的全微分，记作$dz$，即

$$dz=A\Delta x+B\Delta y$$

2.三者关系

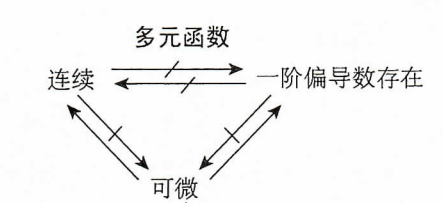
3.关系证明

3.1 偏导和连续

1. 可导不一定连续

   对于不成立的推导，我们只需举出一个反例即可

   $$f(x,y)=\{\begin{array}{ll}\frac{xy}{x^2+y^2}& (x,y)\ne (0,0)\\ 0& (x,y)=(0,0)\end{array}$$

   由于

   $$f_x^{\prime }(0,0)=li{m}_{\Delta x\to 0}\frac{f(\Delta x,0)-f(0,0)}{\Delta x}=li{m}_{\Delta x\to 0}\frac{0-0}{\Delta x}=0$$

   同理$f_y^{\prime }(0,0)=0$, 故$(0,0)$点可导, 设点P为聚点，当点P沿着平行于$y=kx$的方向趋于与$(0,0)$时，

   $$li{m}_{x\to 0,y\to kx}=li{m}_{x\to 0}\frac{k{x}^2}{x^2+k^2{x}^2}=\frac{k}{1+k^2}$$

   该极限不存在，则$f(x,y)$在$(0,0)$点不连续

2. 连续不一定可导

   对于不成立的推导，我们只需举出一个反例即可

   $$f(x,y)=|x|+|y|$$

   由$li{m}_{x\to 0,y\to 0}f(x,y)=li{m}_{x\to 0,y\to 0}(|x|+|y|)=0=f(0,0)$,知$f(x,y)$在$(0,0)$点连续

   而$f(x,0)=|x|$在$x=0$处不可导，则$f_x^{\prime }(0,0)$不存在，由对称性知$f_y^{\prime }(0,0)$也不存在，故函数不可导

3.2 可微和偏导

1. 可微一定偏导

   设函数$z=f(x,y)$在点$P(x,y)$可微分，于是对于点P的某个领域内的任意一点$P^{\prime }(x+\Delta x,y+\Delta y)$式

   $$\Delta z=A\Delta x+B\Delta y+o(\rho )$$

   总成立。特别的,当$\Delta y=0$时，$p=|\Delta x|$，所以上式成为

   $$f(x+\Delta x,y)-f(x,y)=A\Delta x+o(|\Delta x|)$$

   上式两边各除$\Delta x$，再令$\Delta \to 0$而取极限，就得

   $$li{m}_{\Delta x\to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}=A$$

   从而偏导数$\frac{\partial f}{\partial x}$存在，且等于A，同理可证$\frac{\partial z}{\partial x}=B$，证毕

2. 偏导不一定可微

   对于不成立的推导，我们只需举出一个反例即可

   $$f(x,y)=\{\begin{array}{ll}\frac{xy}{\sqrt{x^2+y^2}}& (x,y)\ne (0,0)\\ 0& (x,y)=(0,0)\end{array}$$

   由于

   $f_x^{\prime }(0,0)=li{m}_{\Delta x\to 0}\frac{f(\Delta x,0)-f(0,0)}{\Delta x}=li{m}_{\Delta x\to 0}\frac{0-0}{\Delta x}=0$

   同理$f_y^{\prime }(0,0)=0$, 故$(0,0)$点可导，但

   $li{m}_{\Delta x\to 0,\Delta y\to 0}\frac{[f(\Delta x,\Delta y)-f(0,0)]-[f_x^{\prime }(0,0)\Delta x+f_y^{\prime }(0,0)\Delta y]}{\rho }=li{m}_{\Delta x\to 0,\Delta y\to 0}\frac{\Delta x\Delta y}{(\Delta x{)}^2+(\Delta y{)}^2}$

   设$g(x,y)=\frac{xy}{x^2+y^2}$, 设点P为聚点，当点P沿着平行于$y=kx$的方向趋于与$(0,0)$时，

   $li{m}_{x\to 0,y\to kx}=li{m}_{x\to 0}\frac{k{x}^2}{x^2+k^2{x}^2}=\frac{k}{1+k^2}$,该极限不存在，则$f(x,y)$在$(0,0)$点不可微

3.3 可微和连续

1. 可微一定连续

   若$z=f(x,y)$在点$(x,y)$可微分，那么由微分的定义有

   $$li{m}_{\rho \to 0}\Delta z=0$$

   从而

   $$li{m}_{\Delta x\to 0,\Delta y\to 0}=f(x+\Delta x,y+\Delta y)=li{m}_{\rho \to 0}[f(x,y)+\Delta z]=f(x,y)$$

   因此$z=f(x,y)$在点$(x,y)$处连续

2. 连续不一定可微

   同上举反例即可

   $$f(x,y)=|x|+|y|$$

   由3.1.2知$f(x,y)$在$(0,0)$点连续且函数不可导，而因为偏导存在是全微分的必要条件, 因此也不可微

4.记忆方法

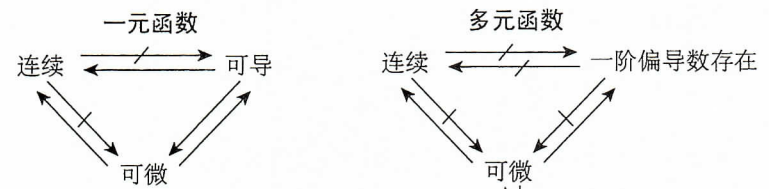
与一元函数连续可导可微对比记忆即可(一元函数关系可参考笔者上一篇文章), 两者的区别在于

1. 多元函数偏导(可导)推不出连续
2. 多元函数偏导(可导)推不出可微

其余部分都相同,那么为什么二元函数偏导推不出连续和可微呢? 下面从几何角度证明

函数可导,即偏导数$f_x(x_0,y_0)$,$f_y(x_0,y_0)$存在

而$f_x(x_0,y_0)$本质上是$f(x,y_0)$函数的导数,把$y$用$y_0$代进去,现在只有$x$在变化,而$x$在变化的时候,只能在$y=y_0$的线上变化, 如下图$f_x(x,y_0)$

这说明这点偏导数只跟这个二元函数沿$y=y_0$这条线上函数值有关

同理,代入$x_0$,这点的另一个偏导数只跟二元函数沿$x=x_0$这条线上函数值有关, 如下图$f_y(x_0,y)$

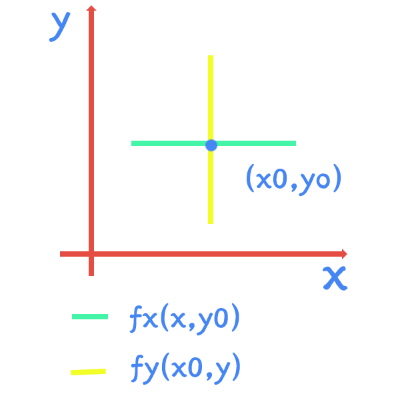
以上说明两个偏导数只跟过$(x_0,y_0)$点平行于两个坐标轴的十字线有关.

但连续是要求动点以任意方式趋向$(x_0,y_0)$的极限等于$(x_0,y_0)$点函数值$f(x_0,y_0)$.

故十字线上的函数值决定不了函数的重极限

同理,决定不了全微分

5.参考文章

1. 高等数学第七版下册
2. 武忠详辅导讲义