在多元的情况下,可微可导的关系要比在一元情况下复杂,但是只是要复杂一些,如果我们从一元开始去理解,你会发现并不困难。
这篇文章主要阐述以下三个概念:偏微分
偏导数
全微分
全导数这里暂时不讲,看名字好像和全微分关系很大,其实和“方向导数”的关系更大,所以留到讲“方向导数”的时候再一起来说。
1 偏微分
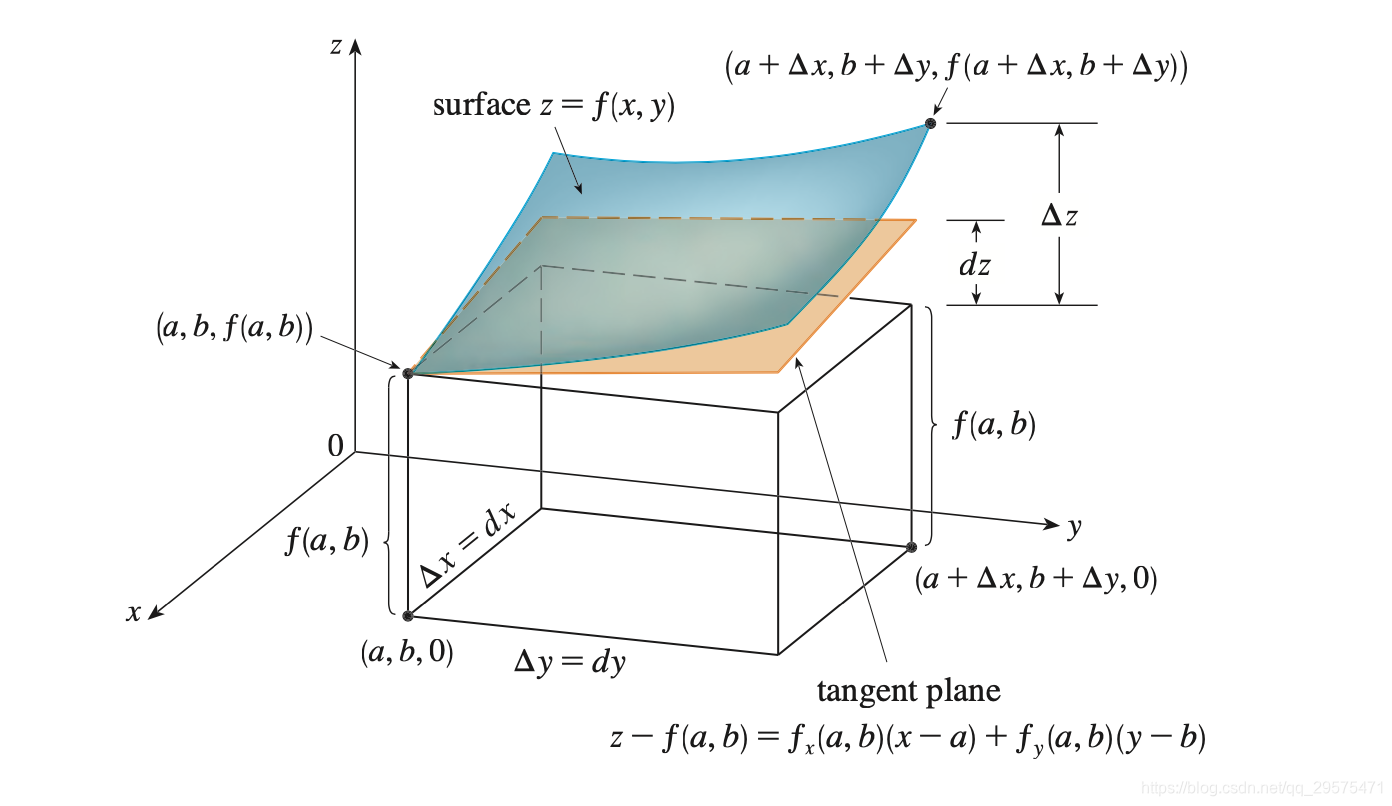
在一元函数中的微分就是函数的切线:
关于微分就是切线,我写的很多文章(比如我最近的 如何通俗解释全微分? )都希望大家可以理解这一点,虽然要严格讲清楚需要微分几何、流型的知识,但是我认为掌握了这一点对于我们学习微积分很有帮助。
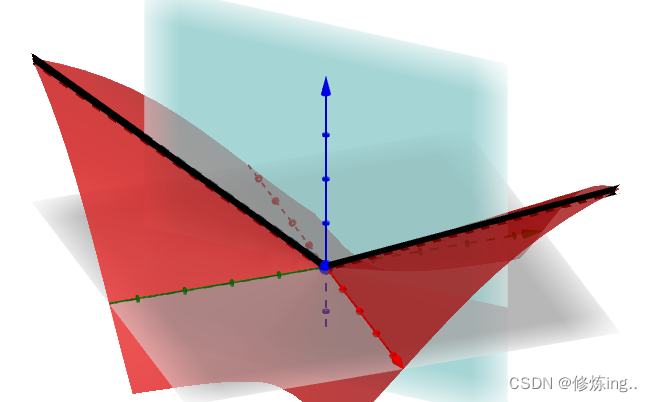
我们发挥一下空间想象力,把它从平面中拽出来,进入三维空间:
之前是平面曲线,现在是空间曲线。切线仍然是切线,微分仍然是微分。
我们再想象一下,其实这个空间曲线是
这个空间平面与
这个空间曲面的交线:
我们就把这个切线称为
对于
的偏微分。为什么是对于
的呢?因为这是
与
的交线,在这条线上无论点怎么变化,都要满足