霍夫曼树
霍夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。
所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。
树的路径长度 WPL 是从树根到每一结点的路径长度之和,记为
N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明霍夫曼树的WPL是最小的。
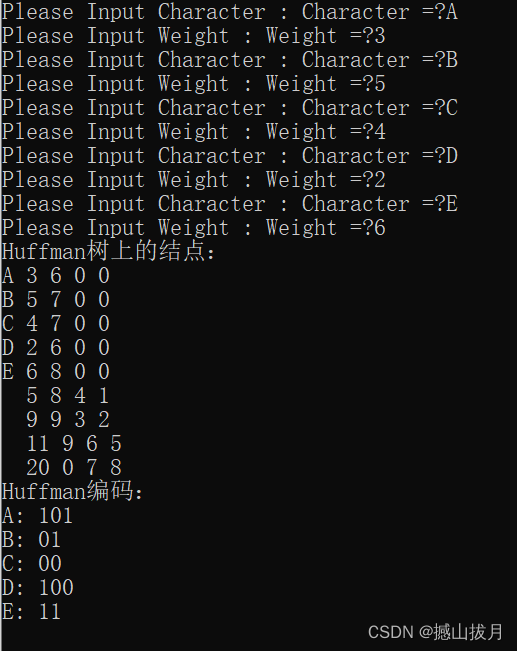
假设有n个权值,则构造出的哈夫曼树有n个叶子节点.n个权值记为{w1,w2,w3...wn},哈夫曼树的构造过程为:
- 将w1,w2,w3...wn看成具有n棵树的森林,每棵树仅有一个节点。
- 从森林中,选取两棵根节点权值最小的树,两棵树分别作为左子树与右子树,构建一棵新树。新树的权值等于左右子树权值之和。
- 从森林中删除两棵权值最小的树,将构建完成后的新树加入森林中。
- 重复2、3步骤,直到森林只剩一棵树为止。这棵树便是哈夫曼树。
霍夫曼编码
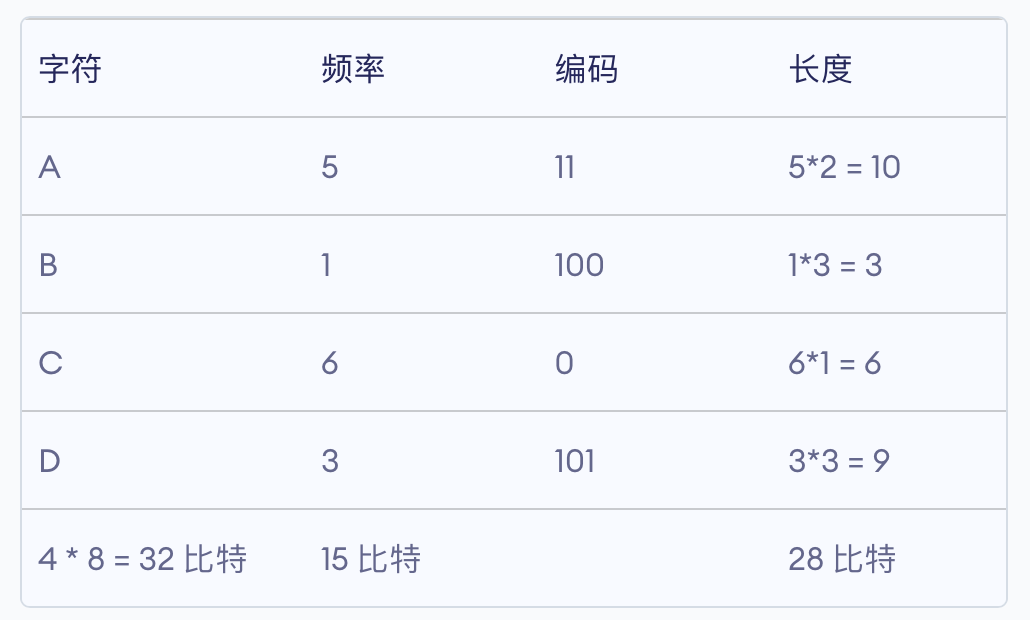
从根节点到每一个叶子节点的路径上,左分支记为0,右分支记为1,将这些0与1连起来即为叶子节点的哈夫曼编码。
霍夫曼编码,对于出现频率越高的字符(也即权值越大),其编码越短。这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
由此得到的德霍夫曼编码为前缀码,即任何一个字符的编码都不能是其他字符编码的前缀。
根据此特性,通过对编码前几位与字符编码对比,匹配不成功则增加匹配字符的长度,匹配成功则对编码下几位进行匹配,可得到相应解码。
完整代码
本次的代码只实现输入字符串后,对本字符串进行霍夫曼编码解码。
#include<iostream>
#include<string>
#include<list>
#include<algorithm>
#include<fstream>
using namespace std;class node
{public:node *left;node *right;string code; //编码char data;int value; //权值node(){left=NULL;right=NULL;value=0;}
};
struct cmp //函数对象 ,用于list的sort函数
{bool operator()(const node * x, const node* y ){return x-> value < y-> value;}
};int getnode(char data,int value,list<node*> &res)
{node *temp=new node; //每个数据生成一个结点temp->data=data;temp->value=value;res.push_back(temp);return 0;
}int getnewnode(list<node*> &res) //取两个权值最小的结点生成新的结点
{node *left=new node; //最小的取为左子树left=res.front();res.pop_front() ;node *right=new node; //第二小的取为右子树right=res.front();res.pop_front() ;node *cur=new node; //创建新节点,连接左右子树cur->value=left->value+right->value;cur->left=left;cur->right=right;res.push_back(cur);return 0;
}void nodecode(node* cur,list<node*> &cod) //为每个叶子结点进行编码
{if(cur->left!=NULL){cur->left->code="0"+cur->code;nodecode(cur->left,cod);}if(cur->right!=NULL){cur->right->code="1"+cur->code;nodecode(cur->right,cod);}if(cur->left==NULL&&cur->right==NULL){reverse(cur->code.begin(),cur->code.end());cod.push_back(cur); //每个叶子结点加到list中cout<<cur->data<<":"<<cur->code<<endl;}
}void Hofmanntreecode (node* cur,list<node*> &res) //霍夫曼树编码
{cur->left->code="0";cur->right->code="1";nodecode(cur->left,res);nodecode(cur->right,res);
}string Hofmannencode(int fre[128],string a ,list<node*> &res) //霍夫曼编码,参数:26个字母出现次数,目标字符串,霍夫曼树结点list
{int count=0; //有效字符数 for(int i=0; i<128; i++) //字符生成结点{if(fre[i]!=0){getnode(char(i),fre[i],res);count++;}}for(int i=0; i<count-1; i++) //选取权值最小的两个生成新结点{res.sort(cmp());getnewnode(res);}node *cur=new node; //为每个叶子结点编码cur=res.front();res.clear();Hofmanntreecode(cur,res);string code[128];for(list<node*>::iterator it=res.begin(); it!=res.end(); it++) //得到每个字符的编码 {code[(**it).data]=(**it).code;}string result;for(int i=0; i<a.length(); i++) //进行编码 {result+=code[a[i]];}return result;}string getstring(string yourstring, int pos1, int pos2 ) //字符串切片,得到字符串从pos1到pos2位置的字符串,不包括pos2
{string result;for(int i=pos1; i<pos2; i++){result+=yourstring[i];}return result;
}string Hofmanndecode(string result,string code[128]) //霍夫曼解码,参数:26个字母编码
{string decode;int pos=0;int max=1;for(int i=0; i<128; i++){if(max<code[i].length())max=code[i].length();}while(pos<result.length()){for(int i=0; i<128; i++) //每几个编码与字母的编码匹配{for(int x=1; x<=max; x++) //有x个编码一起匹配,知道超出字母最长的编码或者匹配到{if(getstring(result,pos,pos+x)==code[i]){pos+=x; //移动x个位置decode+=char(i); //进行解码 break;}}}}return decode;}int main(void)
{list<node*> res;string yourstr;getline(cin,yourstr);int fre[128];for(int i=0; i<128; i++) //初始化{fre[i]=0;}for(int i=0; i<yourstr.length(); i++) //统计每个字母出现的次数{fre[yourstr[i]]++;}string result;result=Hofmannencode(fre,yourstr,res); //霍夫曼编码,参数:26个字母出现次数,目标字符串,霍夫曼树结点liststring code[128];while(!res.empty()){code[res.front()->data]=res.front()->code;res.pop_front();}string decode;decode=Hofmanndecode(result,code); //霍夫曼解码,参数:26个字母编码cout<<" text :"<<yourstr<<endl;cout<<"encode:"<<result<<endl;cout<<"decode:"<<decode;
}
输入:
I love you, but you don't love me!
输出:
:00
l:0100
t:0101
v:0110
y:0111
!:10000
':10001
,:10010
I:10011
b:10100
d:10101
m:10110
n:10111
o:110
e:1110
u:1111
text :I love you, but you don't love me!
encode:10011000100110011011100001111101111100100010100111101010001111101111001010111010111100010101000100110011011100010110111010000
decode:I love you, but you don't love me!




![[基础知识] 霍夫曼编码](https://img-blog.csdnimg.cn/img_convert/4834d96399827c682209c82f6ea87470.gif)