先摘一下百科的说法

        “哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）。”

霍夫曼编码应用十分广泛，比如最常见的JPEG中就应用这种方法。霍夫曼编码是基于霍夫曼树的一种编码方式。

霍夫曼树

霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的 路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+...+Wn*Ln)，N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明霍夫曼树的WPL是最小的。比如

构造方式

霍夫曼树的构造方式也是基于这种权重比较进行构造的，具体步骤是：

(1)  根据给定的 n 个权值 {w1,w2, … wn} 构成 n 棵二叉树的集合  F = {T1,T2, … Tn}，其中每棵二叉树 Ti 中只有一个权值为 wi 的根结点。
(2)  在 F 中选取两棵根结点权值最小的树作为左、右子树构造一棵新的二叉树，且置新二叉树的根结点的权值为其左、右子树根结点的权值之和。
(3)  在 F 中删除这两棵树，同时将新得到的二叉树加入集合 F 中。

(4)  重复 (2) 和 (3) ，直到 F 中只含一棵树为止。

下面来举个例子~

4 个叶子结点 a、b、c、d，分别带权7、5、2、4。构造流程画图说明一下：

霍夫曼编码

相信通过以上内容，对霍夫曼树有了基本了解，下面开始介绍基于霍夫曼树的编码

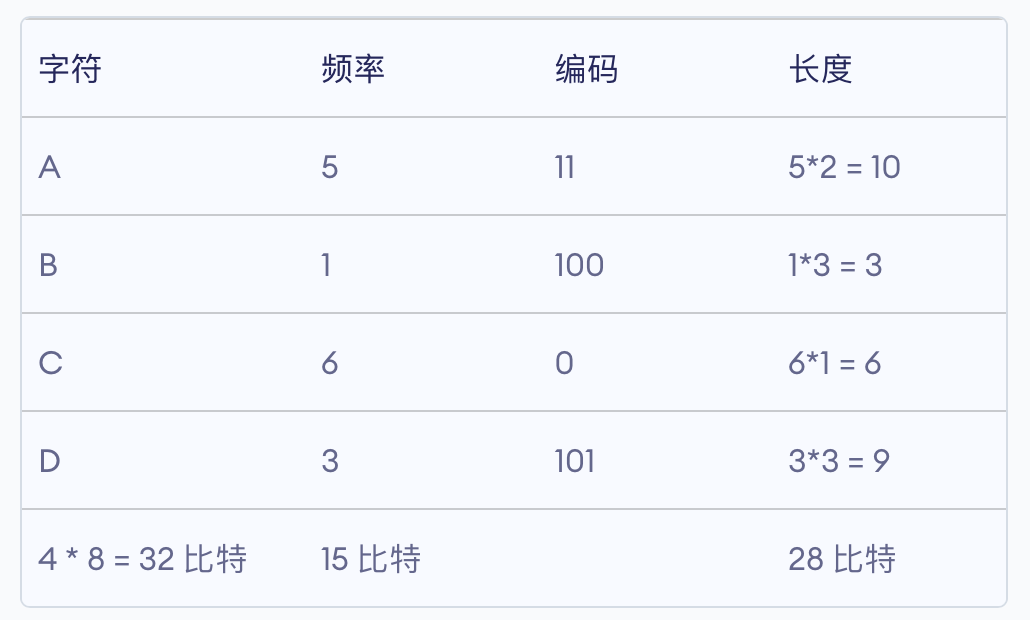
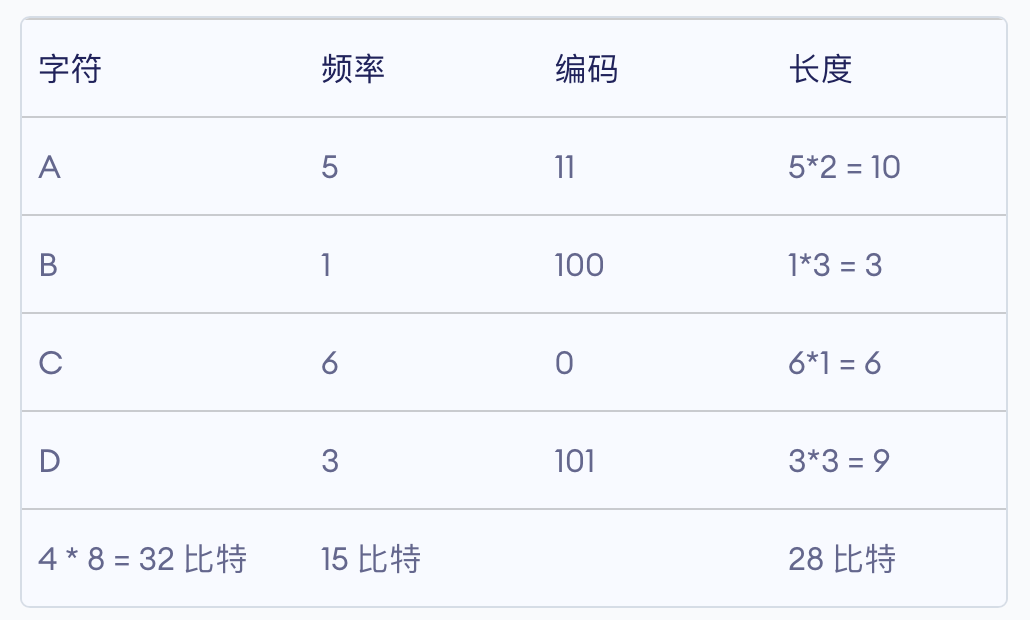
我们都知道，计算机是基于电信号通断的二进制数据流信息传输，比如我们要传输一串字符“ABCDEBCDBB”，我们就要用01组合来表示所有的字符，显然该字符串里有5种字符，2^2 < 5< 2^3，所以我们需要至少三位二进制表示所有的字符这样一来表示这串十个字符的信息就要使用10 * 3 = 30个数，再看这串字符，不难发现B，C，D的使用频率很高，那么如果我们提供一种方法使表示信息中常用字符的编码减少，那么整体的编码长度肯定会大大减少。比如如果我们可以用2位来表示B，C，D，即使这样的代价是使用4位编码来区分余下的A，E，那么总编码长度为 2 * 4+8 *2 = 24，相对于30个数的编码有了显著的减少，对于十个字符的信息都能有着显著的成效，那么实际中成千上万的信息肯定会大大减少编码量。

霍夫曼编码就是基于这种思想应运而生，上文中介绍的霍夫曼树节点的权重，就是实际编码中每个字符的出现频率，为了更好地学习霍夫曼编码，首先我们介绍一下前缀编码的概念：

若设计的长短不等的编码，满足任一个编码都不是另一个编码的前缀，则这样的编码称为前缀编码。举个例子~

假设 A , B , C , D 前缀编码可以为  0 , 110 , 10 , 111，利用二叉树设计二进制前缀编码如下图

叶子结点表示 A , B , C , D 这 4 个字符左分支表示 ‘0’，右分支表示 ‘1’从根结点到叶子结点的路径上经过的二进制符号串作为该叶子结点字符的编码路径长度为编码长度，证明其必为前缀编码，即依照前缀编码进行判断不会有走错路的多余情况

霍夫曼编码就是根据字符出现频率（次数），映射为叶子节点权重，建立霍夫曼树，设立0/1路径，得到前缀编码的过程，

举个例子~

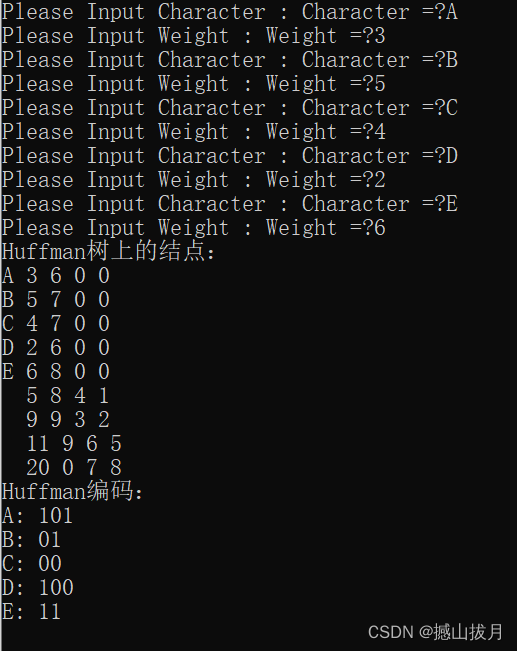
某通信可能出现 A B C D E F G H 8 个字符，其概率分别为 0.05 , 0.29 , 0.07 , 0.08 , 0.14 , 0.23 , 0.03 , 0.11 ，试设计Huffman编码

过程如下：

设  w = { 5 , 29 , 7 , 8 , 14 , 23 , 3 , 11 }

这样就得到了霍夫曼树~然后我们令左子树为0，右子树为1，

到达每个叶子（字符）的序列（顺序是根节点->...->叶子）就是每个字符的编码啦~

霍夫曼解码过程

解码过程就是编码过程的逆过程，对于确定的一串霍夫曼编码，从根节点开始沿着编码中的二进制顺序找到叶子节点获取字符，应用前缀编码的特性，解码出一个字符又重新开始从根节点进行下一次解码，不存在错误路径或是冗余操作~

霍夫曼编码解码与压缩解压缩

既然霍夫曼编码可以缩短序列，那么我们就可以应用这种编码替代原有的存储码值，实现文本形式文件的压缩与解压缩，由于过程中牵扯的类比较多，涉及基本都是代码的内容，所以另开一篇，有兴趣请移步我的另一篇博文