基础理解

什么是哈夫曼树（Huffman Tree）

        给定N个带权值的叶子节点，如何构造出一个带权路径最小的二叉树？

在数据结构理论中，哈夫曼树又称为最优树，相关的知识点还有哈弗曼编码等。在正式介绍哈夫曼树之前，需要知道下面的知识点：

（1）节点路径

按照规定，将树中一个节点到另一个节点所经历的分支，称为节点路径，比如上图中节点A到节点E的路径为ABE。

（2）路径长度

根据上述“节点路径”的定义，将路径上的分支总数称为路径长度，比如上图中节点A到节点E的路径长度为2。

（3）节点的带权路径长度

根据上述“节点路径”和“路径长度”的定义，将从根节点到某节点的路径长度和节点权值的乘积，称为节点的带权路径长度。比如上图中节点A到节点D的路径长度为2，权值为8，则带权路径长度为2x8=16。

（4）树的带权路径长度

根据上述“节点的带权路径长度”的定义，将树中所有叶子节点的带权路径长度，称为树的带权路径长度。比如上图中，三个叶子节点C、D、E，对应的路径长度分别为1、2、2，对应的权值分别为4、8、3，则树的带权路径长度为：

将上述概念形式化，可以使用下面的公式进行计算：

其中了表示路径长度，w表示权值，n表示叶子节点个数。

什么是哈夫曼编码(Huffman Coding)

又称霍夫曼编码，是一种编码方式，可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）。

哈夫曼编码，主要目的是根据使用频率来最大化节省字符（编码）的存储空间。

简易的理解就是，假如我有A,B,C,D,E五个字符，出现的频率（即权值）分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树，即取1，2构成新树，其结点为1+2=3，如图：

虚线为新生成的结点，第二步再把新生成的权值为3的结点放到剩下的集合中，所以集合变成{5,4,3,3}，再根据第二步，取最小的两个权值构成新树，如图：

再依次建立哈夫曼树，如下图：

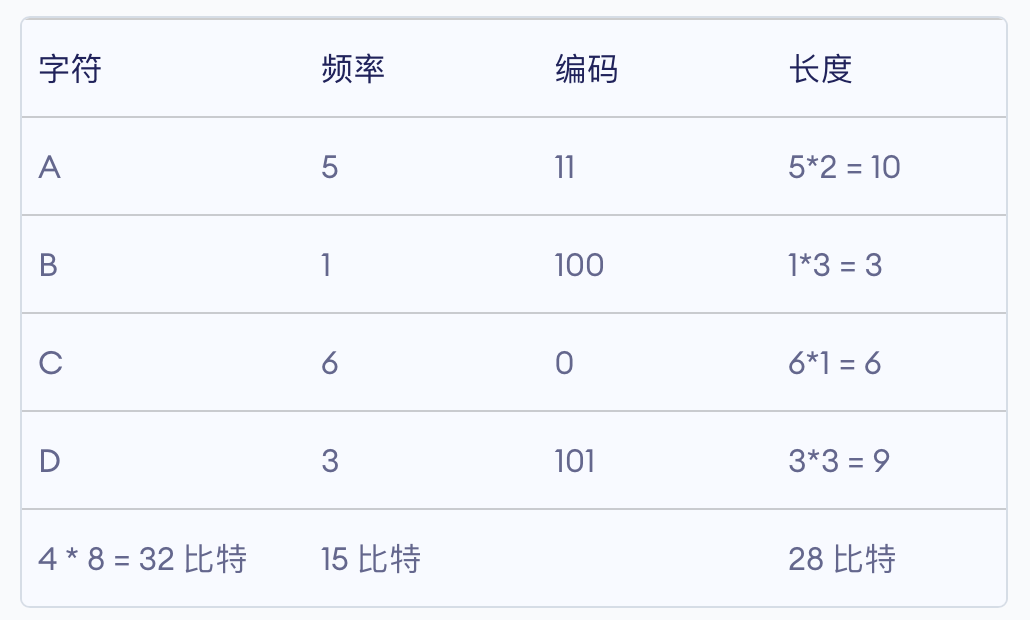
其中各个权值替换对应的字符即为下图：

所以各字符对应的编码为：A->11,B->10,C->00,D->011,E->010
霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩，加密解密等场合。

如果考虑到进一步节省存储空间，就应该将出现概率大（占比多）的字符用尽量少的0-1进行编码，也就是更靠近根（节点少），这也就是最优二叉树-哈夫曼树。
为什么？-----> 权值大的在上层，权值小的在下层。满足出现频率高的 码长 短。

哈夫曼编码的带权路径权值：叶子节点的值 * 叶子节点的高度（根节点为0）

深入研究

1、什么是哈夫曼编码？

在数据传送时，信息表现为0和1的二进制形式。为了提高传输的速度，可以采用变长的编码方式，寻找更优的编码方式。同时，必须要保证编码不存在二义性（任意字符编码都不是其它字符编码的前缀）。

哈夫曼编码就是符合上述要求的编码方式，采用自底向上的形式构造哈夫曼树。按照字符的概率分配码长，实现平均码长最短的编码。

2、如何进行哈夫曼编码？

使用需要传送的字符构造字符集C = {c1, c2, ... cn}，并根据字符出现的频率构建概率集W = {w1, w2, ... wn}。哈夫曼编码的流程如下：

• 将字符集C作为叶子节点；
• 将频率集W作为叶子节点的权值；
• 使用C和W构造哈夫曼树；
• 对哈夫曼树的所有分支，左子树分支编码为0，右子树分支编码为1；

通过上述流程，即完成了哈夫曼编码。

3、哈夫曼编码的例子？

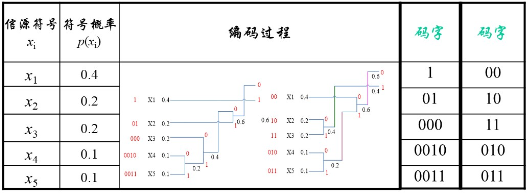
首先，设定字符集为C = {T1, T2, T3, T4}，对应的频率集为W = {2, 3, 7, 5}，可以构造出下面的哈夫曼树（参见前面3篇文章）：

构造出哈夫曼树后，只需要将左子树分支编码为0，右子树分支编码为1，即可获得哈夫曼编码如下：

4、哈夫曼编码方式有哪些？

对叶子节点进行Huffman编码共有两种方式，第一种是从根节点访问到叶子节点，第二种是从叶子节点访问到根节点（叶子节点具有parent数据成员，可以访问到其父节点）。

5、哈夫曼编码整体流程是什么？

含有4个字符（叶子节点）时，需要进行n-1次合并完成哈夫曼树的合并：

经过n-1次合并后，生成n-1个新的节点，最后生成的节点为哈夫曼树的根节点：

（1）创建长度为2n-1的哈夫曼树数组，含有n个叶子节点

（2）创建长度为n的string数组，用于存放n个叶子节点的哈夫曼码

（3）从某叶子节点开始，不断寻找其父节点，直到寻找到根节点，并对此路径上每个分支进行编码，左孩子为0，右孩子为1

6、如何从叶子节点访问到根节点？

从任意叶子X节点（数组前n项中的某一项）开始，根据X的parent值（即X的父节点在数组中的位置）找到其父节点。

找到X的父节点后，根据父节点的left和right值判断X和父节点的关系。如果X是父节点的左子树，则编码为1；如果X是父节点的右子树，则编码为0。

编码函数如下：

void HuffmanCode(Node *p, const int numLeafs, string *codes) {// p为节点数组的指针，codes为string数组的指针 // 用于存储每个节点的哈夫曼码// parent表示父节点位置int parent;// 每次对一个叶子节点进行编码// i表示当前叶子节点位置for (int i=0; i < numLeafs; i++) {// j表示当前节点位置，i是不能在下面循环中改变的// 使用j来记录节点的移动过程int j = i;// 当前节点的父节点位置parent = p[i].parent;// 从当前叶子节点p[i]开始，找到哈夫曼树的根节点// 循环结束条件是此时parent为0，即达到哈夫曼树的根节点while(parent != -1) {// 如果当前节点是父节点的左子树，则此分支编码为0if (p[parent].left == j) {codes[i].push_back('0');}// 如果当前节点是父节点的右子树，则编码为1else {codes[i].push_back('1');}j = parent;parent = p[j].parent;}cout << codes[i] << endl;}
}