霍夫曼编码

基本介绍

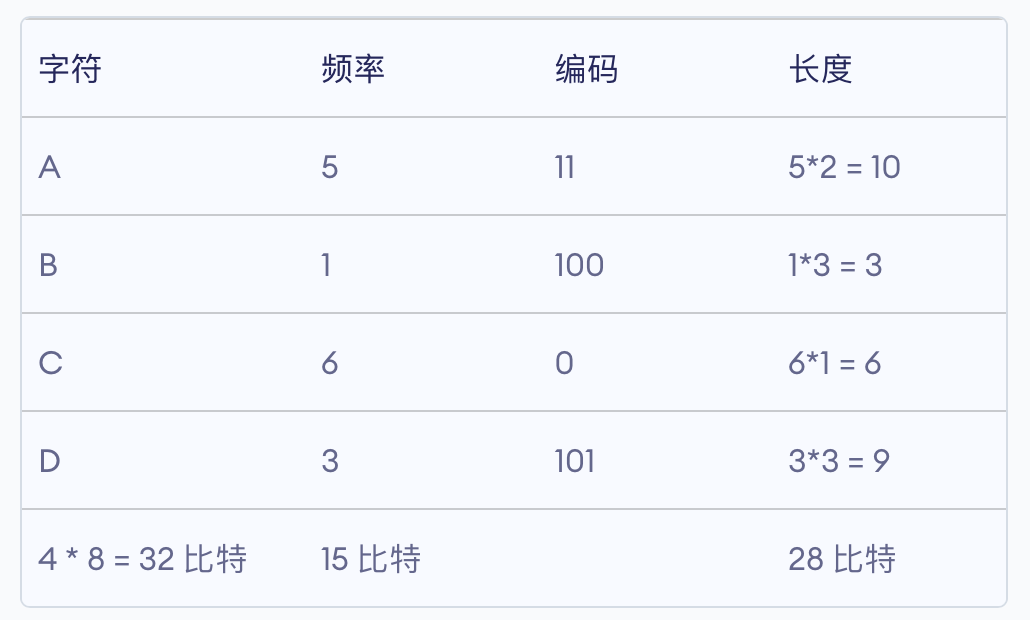
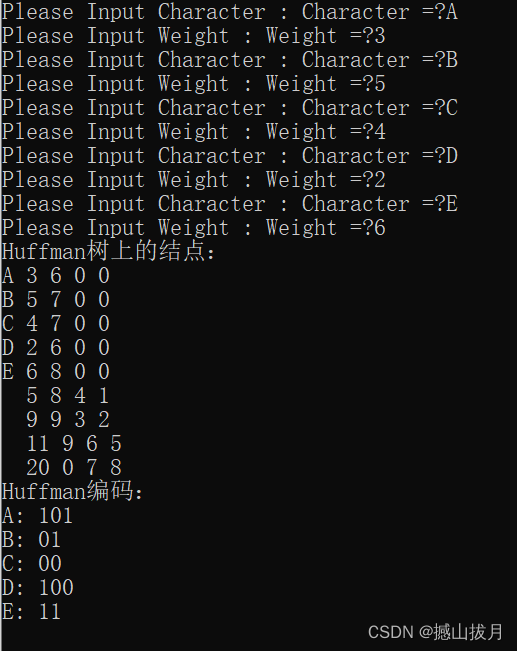
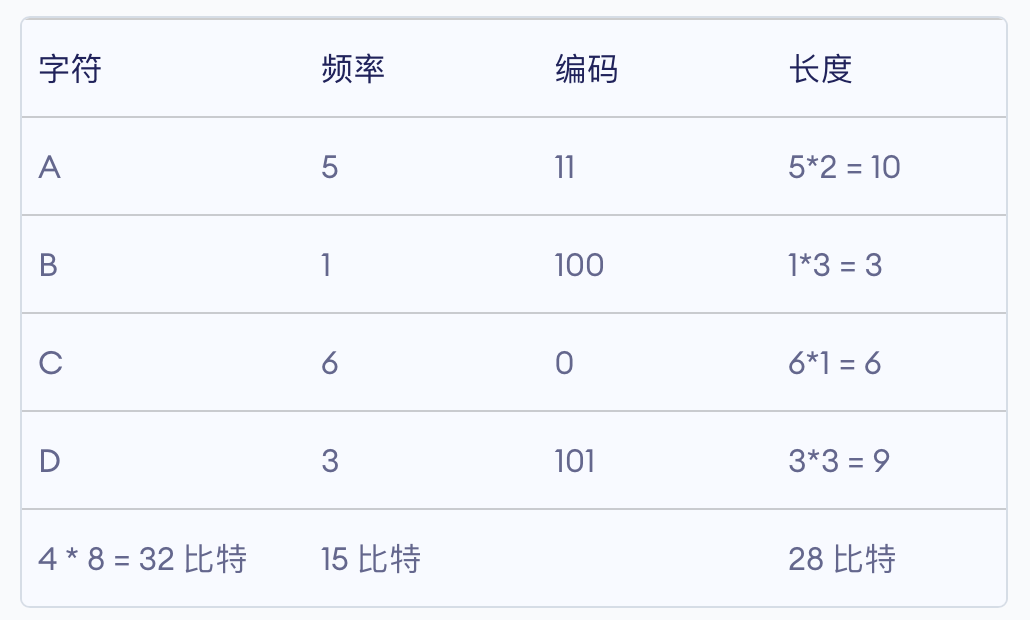
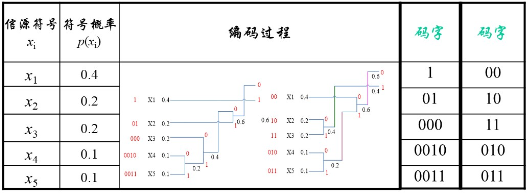
1. 霍夫曼编码是一种编码方式，属于一种程序算法
2. 霍夫曼编码是霍夫曼树在通讯领域的经典应用之一
3. 霍夫曼编码广泛用于数据文件的压缩，压缩率通常在20% 到90%，通常数据的重复率越高，那么压缩率就越高
4. 霍夫曼编码是可变字长编码（VLC）的一种，由霍夫曼提出，又称之为最佳编码

通讯领域中常用的编码方式

1. 定长编码

• 对原始数据不加任何的修改，原原本本按照对应的编码集，转成二进制代码进行存储。占用空间大。
  

2. 变长编码

• 按照字符出现的次数进行编码，原则上是出现的次数越多，则编码越小。
• 是比较简洁，但是会出现多义性，因为代码彼此之间有重复。
• 前缀编码：字符的编码不是其余字符编码的前缀。
  

3. 霍夫曼编码

• 对所给字符串的各个字符出现的个数进行统计
• 按照上面字符出现的次数构建霍夫曼树，次数作为权值，同时你的节点上要有所代表的字符。
• 根据霍夫曼树给各个字符进行编码：
  • 向左的路径为0，向右的路径为1
  • 根据到达给节点的路径确定该节点代表字符的编码
  • 生成的编码是前缀的编码，每一个编码都不会是另外一个字符的前缀。致使在匹配的时候不会出现多义性
• 按照上面的霍夫曼编码，将原先的字符换转换成编码。此编码是前缀编码，不会出现多义性，同时又对在定长编码编译情况下原长码进行压缩处理，是无损压缩。
• 
• 问题：当有大量的字符是相同的出现次数时，相同权值的不同叶子节点可能排在不同的位置，形成不同的霍夫曼树，故而形成不同的代码，但是WPL始终是相同的，所以没有必要担心。最终形成的压缩文件的大小一定相同，因为WPL始终是相同的。

思路分析

1. 梗概：将每一个字符本身的ASCII码和其出现的次数两者结合，以出现的次数为权构建霍夫曼树，再根据到达对应节点的路径生成对应的霍夫曼编码。
2. 总体步骤：构建相应的霍夫曼树——》遍历读取生成相应的霍夫曼编码
3. 具体分析

• 节点类：在满足基本节点的特征的基础上，必须把出现的次数作为权值，结点必须包含其本身代表的字符的ASCII码值。同时涉及到构建霍夫曼值，所以必须实现Comparable接口
• 主类中：
  • 将所给的字符串生成字节型数组
  • 将字节型数组根据自身的内容和出现的次数，生成对应的Node结点（用Map类处理计数），然后转成包含Node的集合类对象list
  • 生成霍夫曼树
  • 遍历霍夫曼树生成对应的霍夫曼编码

代码实现

1. Code类：

class Node implements Comparable<Node>{Byte date;//表示字符对应的ASCII码int weight;//表示对应字符出现的次数Node left;Node right;public Node(Byte date, int weight) {this.date = date;this.weight = weight;}@Overridepublic int compareTo(Node o) {return this.weight - o.weight;}@Overridepublic String toString() {return "Node{" +"date=" + date +", weight=" + weight +'}';}public void preOrder(){if (this != null){System.out.println(this);}if (this.left != null){this.left.preOrder();}if (this.right != null){this.right.preOrder();}}
}

2. 主类中

• 统计各字符出现的次数，并将之转换成对应的集合类

private static List<Node> getNodes(byte[] bytes){List<Node> list = new ArrayList<Node>();//创建对应的集合类，用来创建霍夫曼树---每一个对象是节点类Node//遍历对应的生成的Byte【】数组，然后统计一下各个字符出现的次数---用Map类，键值对数据Map<Byte,Integer> counts = new HashMap<Byte,Integer>();for (byte ch : bytes){Integer count = counts.get(ch);//获取出现字节对应的次数if (count == null){//如果对应的Integer是空，说明第一次出现counts.put(ch,1);//再map类中，put是添加，put也是修改}else{//如果对应的Integer不为空，说明已经录入过相应的数字//所以将原来的数字加1counts.put(ch,count + 1);}}//遍历Map类中的每一个键值对，将之生成对应的list类对象for(Map.Entry<Byte,Integer> entry:counts.entrySet()){list.add(new Node(entry.getKey(),entry.getValue()));//key是对应的字符，value是对应的出现的次数}return list;}

• 根据生成的集合类，整理生成对应的霍夫曼树

private static Node huffmanTree(byte[] bytes){List<Node> list = getNodes(bytes);Node left;Node right;while (list.size() > 1){Collections.sort(list);left = list.get(0);list.remove(left);right = list.get(0);list.remove(right);Node parent = new Node(null,left.weight + right.weight);parent.left = left;parent.right = right;list.add(parent);}return list.get(0);}

• 遍历霍夫曼树生成各个叶子节点的对应的路径

static Map<Byte,String> huffmanCodes = new HashMap<Byte,String>();
//存放霍夫曼编码的Map类，公共变量，每一次递归都要存储，所以静态变量
static StringBuilder stringBuilder = new StringBuilder();
//拼接字符串的起点，根节点对应的拼接点
/*** 功能描述：将传入的node节点的所有叶子结点的霍夫曼编码并且放入到霍夫曼编码集合中** @param node 对应的传入待处理的节点，* @param code  分别代码不同方向路径的值，左子节点为0，右子节点为1* @param stringBuilder   用于拼接路径，是不是说一个每一条路都对应了一个个stringbuilder*/private static void getCodes(Node node,String code,StringBuilder stringBuilder){//首先用你传入的Stringbuilder构建一个StringbuilderStringBuilder stringBuilder1 = new StringBuilder(stringBuilder);//一开始就两条路，那就两个，然后每一次走不通的路都会生成不同的值，// 同时还是在上一个节点的基础上进行生成stringBuilder1.append(code);//已经在原先的基础上生成了一个对应的一个stringbuilder，而选择不同的路径也要增加一个code值，代表我走的这条路if (node != null){//如果node等于空就不去处理，说明已经到达结尾，不为空才有相关的值进行判断// 判断当前节点是叶子节点还是非叶子节点if (node.date == null){//说明是非叶子结点，因为本身就没有代表字母//向两边进行递归getCodes(node.left,"0",stringBuilder1);getCodes(node.right,"1",stringBuilder1);}else{//data不为空，说明是叶子节点，进行存储huffmanCodes.put(node.date,stringBuilder1.toString());}}}

• main方法：

 public static void main(String[] args) {String content = "I like Java.Do you like Java?";byte[] contentBytes = content.getBytes();//字符串和字节的区别是什么？字节就是将字符转成为对应的ASCII码，字符就是输出字符的本身getCodes(huffmanTree(contentBytes),"",stringBuilder);System.out.println("生成的霍夫曼编码表" + huffmanCodes);
}

分析与总结

1. 处理处理存在映射关系的两组数据，用Map类，既便于计算出现次数，又便于形成一一对应的关系，用于翻译输出，所以整个过程有两次转换，第一次是在统计各个字符出现的次数，将字节型数组转成Map类；第二次是在由霍夫曼树生成霍夫曼编码时，由树生成Map的编码。
2. 在形成编码的过程中，“边走边成路！”，每一次走不同的结点都会迭代之前的路径生成对应的不同的路径，而路径本身又生成对应的编码。关键点还是还设置一个共有的起点Stringbuilder，共有的记录册HashMap HuffmanCode
3. 总的过程：字符串 —— 》字节型数组——》HashMap<Byte,String>——》ArrayList list——》霍夫曼树——》霍夫曼编码
4. 对于集合类的操作很不流畅，都忘得差不多了，尤其是在遍历键值对的部分关于entry。

复习代码：

package huffmancode;import java.util.*;public class HuffmanCode2 {public static void main(String[] args) {String str = "I have no choice but I have to do!I believe in myself!";byte[] bytes = str.getBytes();//然后将字节型数组生成对应的节点类//将节点类生成霍夫曼树//有霍夫曼树生成对应的霍夫曼编码System.out.println(acquireHuffmanCode(bytes));}//改良，连续调用方法，我自己都晕，将所有的方法封装起来进行调用public static Map<Byte,String> acquireHuffmanCode(byte[] bytes){getHuffmanCode(getHuffmanTree(getNode(bytes)),"",stringBuilder);return HuffmanCode;}//第三部分，有对应的霍夫曼树生成对应的霍夫曼编码//编码Map类承装，设置一个地图碎片的蓝本，用于拼接static Map<Byte,String> HuffmanCode = new HashMap<Byte,String>();static StringBuilder stringBuilder = new StringBuilder();private static void getHuffmanCode(Node2 node2,String code,StringBuilder stringBuilder){StringBuilder stringBuilder1 = new StringBuilder(stringBuilder);stringBuilder1.append(code);if (node2 != null){//说明当前节点不为空，可以斤西瓜下一步的递归操作//节点类型有两种，叶子节点和非叶子节点if (node2.ch == null){//非叶子节点进行左右递归,并且不用判定左右节点是否为空getHuffmanCode(node2.left,"0",stringBuilder1);getHuffmanCode(node2.right,"1",stringBuilder1);}else{//是叶子节点说明已经递归完毕HuffmanCode.put(node2.ch,stringBuilder1.toString());}}}//根据生成的集合list整理生成对应的霍夫曼树private static Node2 getHuffmanTree(List<Node2> list){//生成霍夫曼树就两步，不断重复，排序，建树while (list.size() > 1){//排序Collections.sort(list);Node2 left = list.get(0);Node2 right = list.get(1);list.remove(left);list.remove(right);Node2 parent = new Node2(null,left.val + right.val);parent.left = left;parent.right = right;list.add(parent);}return list.get(0);}//将字节型数组生成对应的节点类private static List<Node2> getNode(byte[] bytes){List<Node2> list = new ArrayList<Node2>();//创建一个集合用来存储转换过后生成的节点Map<Byte,Integer> counts = new HashMap<Byte,Integer>();//调用Map集合类，利用其键值对的存储方式，便于统计书出现次数//遍历字节数组，调用Map类，进行统计for (byte ch:bytes){Integer count = counts.get(ch);//第一次输入，看看是否有对应的数字if (count != null){//如果count不为null，说明已经遍历过了，可以进一部存储counts.put(ch,count + 1);}else{//如果count为null，说明没有遍历过，是第一次出现counts.put(ch,1);}}//统计完数据之后，用来创建对应的节点类for (Map.Entry<Byte,Integer> enty:counts.entrySet()){//说明counts是可以当作数组来及进行遍历list.add(new Node2(enty.getKey(),enty.getValue()));}return list;}}
class Node2 implements Comparable<Node2>{public Byte ch;//对应的字符的字节码int val;//对应字符出现的次数Node2 left;Node2 right;public Node2(Byte ch, int val) {this.ch = ch;this.val = val;}@Overridepublic String toString() {return "Node2{" +"ch=" + ch +", val=" + val +'}';}@Overridepublic int compareTo(Node2 o) {return this.val - o.val;}
}