霍夫曼编码原理以及代码实现

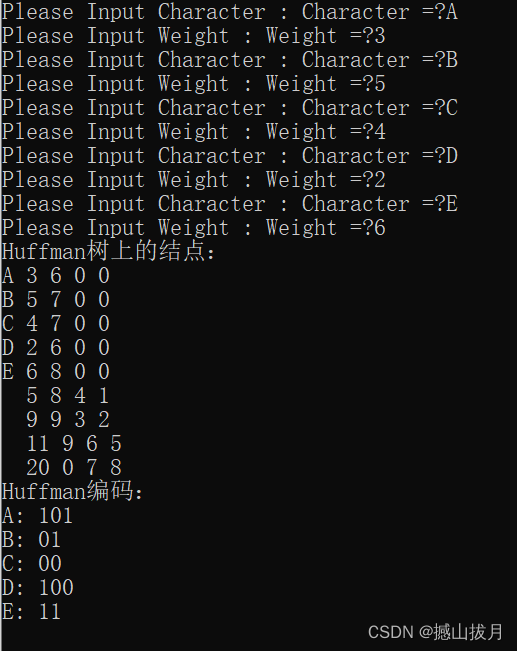
霍夫曼编码压缩能够实现对于自然语言文件空间大幅压缩。对于普通的文本文件字符，简单起见，如果字符为ASCII，则文本中的每个字符使用7bit来表示，如果文本中有大量的重复相同序列，使用ASCII编码来保存存储会造成大量的空间浪费，现在利用霍夫曼编码将文本字符串编码，用较少的比特位表示频率较高的字符，用较多的比特位表示频率较低的字符。

霍夫曼编码的核心思想：

统计文本串的每个字符出现的频率，构造前缀码的单词查找树，根据单词查找树来构造编译表，根据编译表来逐个编码每个字符，得到最终的编码01序列；对于解码，根据编码01序列，结合单词查找树来译码出文本字符串。

前缀码

将字符串每个字符按照特定规则编码成01序列时，同时也需要能够根据01序列，能够译码出原始字符串，要求每个字符的编码都不能是其他字符编码前缀，这样最终编码序列进行译码结果是唯一的，这样的字符编码成为前缀码。ASCII编码每位字符使用7bit来表示是一种定长前缀码，霍夫曼编码是一种变长前缀码，即每个字符的编码长度不一致，频率越高则编码长度越短。

单词查找树

可以使用单词查找树来表示前缀码，单词查找树的叶子结点对应具体的字符，每个节点的左路径看成0，右路径看成1，每个字符的01编码序列为从根路径到该字符叶子结点的路径编码。

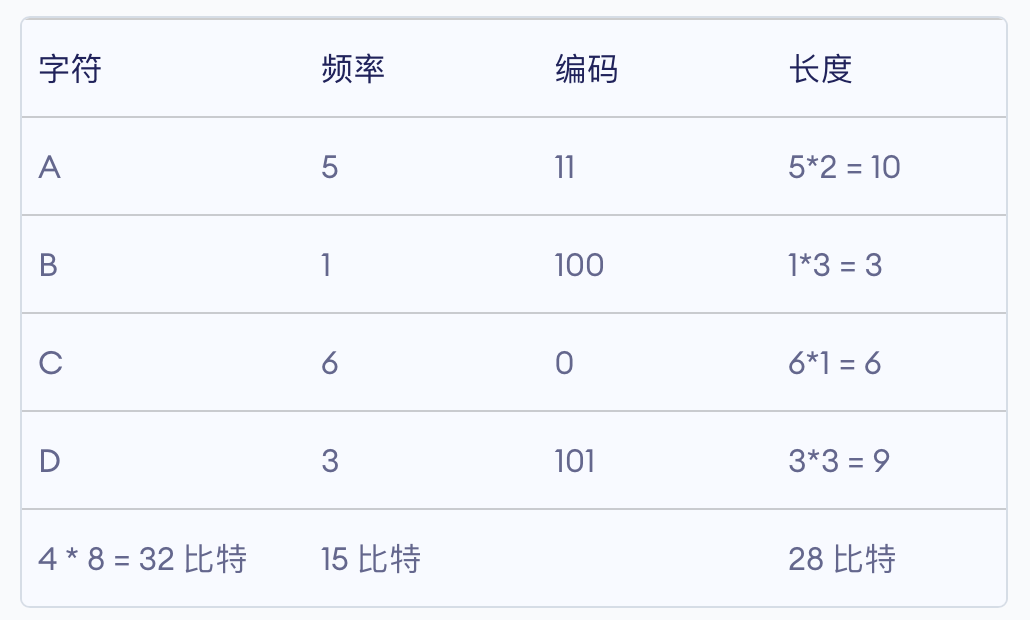
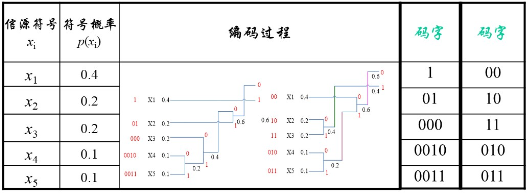
如上所示是对于序列ABRACADABRA!的两种前缀码表示，每个字符编码为根节点到字符叶子结点路径01编码，不同的前缀码压缩后的比特程度不同，霍夫曼编码是一种最优前缀码，即编码后长度最短。

具体霍夫曼树的构造过程如下：

定义霍夫曼树节点数据结构

        //霍夫曼树节点private static class Node implements Comparable<Node>{//叶子节点表示编码字符  非叶子节点为空private char ch;//字符出现的频率private int freq;private final Node left, right;Node(char ch, int freq, Node left, Node right) {this.ch = ch;this.freq = freq;this.left = left;this.right = right;}public boolean isLeaf(){return left==null && right==null;}//后面使用优先级队列来保存Node节点  注意Node节点排序规则  freq小的在前 @Overridepublic int compareTo(Node o) {return this.freq - o.freq;//return o.freq - this.freq;}@Overridepublic String toString() {StringBuilder builder = new StringBuilder();builder.append("Node [ch=");builder.append(ch);builder.append(", freq=");builder.append(freq);builder.append(", left=");builder.append(left);builder.append(", right=");builder.append(right);builder.append("]");return builder.toString();}	}

由于后序要根据节点的字符频率freq来进行排序，因此Node实现Comparable接口。

假定待编码字符串为ASCII字符，取字母表基数为R=256，利用数组索引来统计记录字符以及出现频率的关系。

               char[] input = s.toCharArray();//要压缩的字符串字符个数int total = input.length;//统计字符串中每个字符出现的频率int[] freq = new int[R];for(int i=0; i<total; i++){freq[input[i]]++;}System.out.println("freq = " + Arrays.toString(freq));

霍夫曼树的构造

使用优先级队列，遍历字符索引数组，将出现的字符以及频率，依次加入到优先级队列中并根据出现频率来进行降序排列；

循环操作，每次取出队列中的最小值以及次小值，将两个节点合并成一个新节点，新节点频率为两者之和，新节点左右孩子为两者，将新节点加入到优先级队列中排序，依次循环，直到队列中只有一个节点，此时该节点即为霍夫曼树的根节点。

        private static Node buildTree(int[] freq) {PriorityQueue<Node> pq = new PriorityQueue<>();for(int i=0; i<freq.length; i++){if(freq[i]>0){//System.out.println((char)i);pq.add(new Node((char)i, freq[i], null, null));}}System.out.println("pq = " + pq.toString());while(pq.size()>1){Node l1 = pq.poll();Node l2 = pq.poll();//System.out.println(l1.ch + " " + l1.freq + " " + l2.ch + " " + l2.freq);pq.add(new Node('\0', l1.freq+l2.freq, l1, l2));}			return pq.poll();}

根据编译表进行编码

根据构造的霍夫曼树，从根节点到某一具体的叶子节点，可以获取某一字符对应的01编码序列，遍历所有情况，得到每个字符与编码序列的对应关系，该对应关系即为编译表。利用String[R]来保存每个字符对应的01编码序列，递归思想，如果当前节点为叶子结点则将编码字符串存储在String[R]相应位置，如果当前节点不为叶子节点，则依次进入到左右子树中递归遍历，相应编码字符也要增加0或1，这里0或1是二进制1bit而不是字符'0''1'，这里为了便于表示演示，使用字符来代替。

                //构造编译表  每个字符对应的01序列String[] st = new String[R];buildCode(st, root, "");System.out.println("st = " + Arrays.toString(st));private static void buildCode(String[] st, Node n, String s) {//System.out.println(n);if(n.isLeaf()){st[n.ch] = s;return;}//对于霍夫曼树 左边为0   右边为1//这里的'1'和'0'应为bit 二进制  这里为了显示方便使用字符'1'//'1'字符占用7个bits 而二进制1占用1bitsbuildCode(st, n.left, s+'0');buildCode(st, n.right, s+'1');		}

由编译表，即可以实现对于字符串的编码，遍历字符串的每一个字符x，到编译表String[x]中寻找相应的编码串，组合所有字符编码即可以得到最终编码比特串。

                StringBuilder sb = new StringBuilder();for(int i=0; i<total; i++){//System.out.println(input[i] + "  " + st[input[i]]);sb.append(st[input[i]]);}

根据霍夫曼树进行译码

由编码比特串译码原始字符串，需要使用单词查找树，由于霍夫曼编码是前缀码，对于编码比特串从根节点开始，0进入左子树，1进入右子树，如果某个节点为叶子结点则说明前段比特序列是该字符的编码，将该字符记录；重新从根节点开始继续遍历比特串即可。

        //给定二进制序列   根据霍夫曼树译码public static String expand(String s){StringBuilder sb = new StringBuilder();System.out.println("trieStr = " + trieStr);Node root = readTrie(trieStr);System.out.println("reaftrie = " + root);for(int i=0; i<s.length();){Node x = root;while(!x.isLeaf()){//从字符串中读取每一个字符来模拟读取二进制bitif(s.charAt(i++)=='1'){x = x.right;}else{x = x.left;}}//System.out.println(x.ch);sb.append(x.ch);//i++;}return sb.toString();}

由于编码以及译码场所可能不同，因此为了便于译码，应该将编码过程的单词查找树按照某种规则保存起来，然后译码时根据保存序列再构造出单词查找树。

霍夫曼树存储与加载

霍夫曼树的存储

使用前序遍历，如果节点为非叶子结点记录0，如果为叶子结点记录1和节点字符；频率不需要记录，译码时不需要使用频率，只需要根据比特串寻找从根路径到某个叶子节点即可。

         //由于java  String 特性函数传递不会改变值   private static void saveTrie(Node x, StringBuilder trieStr) {//中序遍历 如果是叶子结点打印1 打印节点字符值  如果是非叶子结点打印0//这里的'1'和'0'应为bit 二进制  这里为了显示方便使用字符'1'//'1'字符占用7个bits 而二进制1占用1bitsif(x.isLeaf()){trieStr.append('1');trieStr.append(x.ch);return;}else{trieStr.append('0');}saveTrie(x.left, trieStr);saveTrie(x.right, trieStr);}

霍夫曼树的加载

使用全局变量index来记录遍历比特串的索引位置，如果比特位1则说明下一个为叶子结点字符，新建一个节点；如果为0，则说明后面为该节点的左右子树序列，递归可以得到最终霍夫曼树。

       //函数指针传递问题  int类型  函数参数传递  值拷贝一次 原来值不变//java函数参数传递问题//实参  形参   实参是对于形参的拷贝  原始类型相当于值拷贝   引用类型相当于引用拷贝//引用拷贝时由于实参引用以及形参引用指向同一个对象，因此形参值会改变实参值//将index值改成全局变量private static Node readTrie(StringBuilder s){index++;if(index>s.length()-1) return null;//System.out.println("index = " + index + " " + s.charAt(index));	if(s.charAt(index)=='1'){//System.out.println("node create = " + s.charAt(index+1));index++;return new Node(s.charAt(index), 1, null, null);}//假定此时index=i 需要进行两个递归调用  进入第一个递归调用  index=i+1   第一个调用返回  此时第二个传值仍为index=i+1//这里的效果应该为第一个调用index=i+1    第二个调用为index=i+2return new Node('\0', 0, readTrie(s), readTrie(s)); }

最终的编码代码

        //根据霍夫曼树  进行编码public static String compress(String s){char[] input = s.toCharArray();//要压缩的字符串字符个数int total = input.length;//统计字符串中每个字符出现的频率int[] freq = new int[R];for(int i=0; i<total; i++){freq[input[i]]++;}System.out.println("freq = " + Arrays.toString(freq));//构造霍夫曼树Node root = buildTree(freq);System.out.println("root = " + root);//构造编译表  每个字符对应的01序列String[] st = new String[R];buildCode(st, root, "");System.out.println("st = " + Arrays.toString(st));//保存解码用的单词查找树saveTrie(root, trieStr);System.out.println("trieStr = " + trieStr.toString());System.out.println("total = " + total);StringBuilder sb = new StringBuilder();for(int i=0; i<total; i++){//System.out.println(input[i] + "  " + st[input[i]]);sb.append(st[input[i]]);}System.out.println("origin length = " + input.length*7);System.out.println("compress length = " + sb.length() + " result = " + sb.toString());return sb.toString();}

最终的译码代码

        //给定二进制序列   根据霍夫曼树译码public static String expand(String s){StringBuilder sb = new StringBuilder();System.out.println("trieStr = " + trieStr);Node root = readTrie(trieStr);System.out.println("reaftrie = " + root);for(int i=0; i<s.length();){Node x = root;while(!x.isLeaf()){//从字符串中读取每一个字符来模拟读取二进制bitif(s.charAt(i++)=='1'){x = x.right;}else{x = x.left;}}//System.out.println(x.ch);sb.append(x.ch);//i++;}return sb.toString();}

测试如下;

                String s = "itwasthebestoftimesitwastheworstoftimesLF";String r = compress(s);String e = expand(r);System.out.println("expand = " + e);System.out.println("code rate = " + r.length()/((double)s.length()*7));

结果如下：

trieStr = 001t001f1h1i001e01w1o01s001m1a001F1L01b1r
total = 41
origin length = 287
compress length = 145 result = 0110010101110111000010110011111010011000101101000001111100100110011001010111011100001011001010101111111111000101101000001111100100110111101111100
trieStr = 001t001f1h1i001e01w1o01s001m1a001F1L01b1r
reaftrie = Node [ch=

这里使用字符‘0’来代替比特0，将字符串编码后得到的字符串实际为比特序列，即字符串长度为比特串长度。可知编码前字符串比特位287，编码后仅为145，编码效率约为50%。

https://github.com/ChenWenKaiVN/TreeSWT/blob/master/src/com/tree/string/compress/Huffman.java