计院2021
1.完全二叉树
给定一颗二叉树,树的每个节点的值为一个正整数。如果从根节点到节点 N 的路径上不存在比节点 N 的值大的节点,那么节点 N 被认为是树上的关键节点。求树上所有的关键节点的个数。请写出程序,并解释解题思路。
例子:
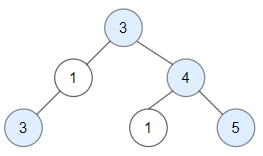
输入: 3, 1, 4, 3, null, 1, 5
输出:4(图中蓝色节点是关键节点)
#include<bits/stdc++.h>
using namespace std;
const int N=100;
int a[N];
int main(){string s;int m=1;while(cin>>s){if(s=="null")a[m++]=-1; else a[m++]=atoi(s.c_str());if(cin.peek()=='\n')break;}int cnt=1;for(int i=2;i<m;i++){if(a[i]==-1)continue;if(a[i]>=a[i/2])cnt++;else a[i]=a[i/2];}cout<<cnt<<endl;return 0;
}2.爬楼梯
训练场上有一个台阶,总共有 n 级。一个运动员可以跳 1 级,也可以跳 2 级。求运动员有多少种跳法。请写出程序,并解释解题思路。
当前台阶,可以由下一层台阶跳一级而来,也可以由下两层台阶跳二级而来
由此可得状态转移方程为dp[i]=dp[i−1]+dp[i−2]。
初始化dp[1]=1,dp[2]=2。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int dp[N];
int n;
int main(){cin>>n;dp[1]=1,dp[2]=2;for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];}cout<<dp[n]<<endl;return 0;
} 3.目标和
给定一个非负整数序列x1,x2,x3…xn,可以给每一个整数取负数或者取原值,求有多少种取法使得这些整数的和等于期望值E。请写出程序,并解释解题思路。
输入:1, 1, 1, 1, 1, 3
输出:5
样例解释:
-1+1+1+1+1 = 3
1-1+1+1+1 = 3
1+1-1+1+1 = 3
1+1+1-1+1 = 3
1+1+1+1-1 = 3
可以将本问题转化为背包问题。期望E=正数和−负数和的绝对值,数据总和sum=正数和+负数和的绝对值。联立方程组可得:正数和 t=(E+sum)/2 ;则原问题转换为,在序列中选择几个数,满足和为t,为经典背包问题。注意,E+sum必须为偶数,否则无解。
dp[i][j]表示从前i个数里选使正整数和为j的方案数;状态转移方程为dp[i][j]=dp[i-1][j]+dp[i-1][j−a[i]] 。
#include<bits/stdc++.h>
using namespace std;
const int N=105,M=1e5;
int a[N],dp[N][M];
int n,E;
int main(){cin>>n;int sum=0;for(int i=1;i<=n;i++){cin>>a[i];sum+=a[i];}cin>>E;int t=(E+sum)/2;if((E+sum)%2!=0){cout<<0<<endl;return 0;}dp[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=t;j++){dp[i][j]+=dp[i-1][j];if(j>=a[i])dp[i][j]+=dp[i-1][j-a[i]]; }}cout<<dp[n][t]<<endl;return 0;
}计院2020
1.斗牛
给定五个 0~9 范围内的整数 a1, a2, a3, a4, a5。如果能从五个整数中选出三个并且这三个整数的和为 10 的倍数(包括 0),那么这五个整数的权值即为剩下两个没被选出来的整数的和对 10 取余的结果,显然如果有多个三元组满⾜和是 10 的倍数,剩下两个数之和对 10 取余的结果都是相同的;如果选不出这样三个整数,则这五个整数的权值为 -1。 现在给定 T 组数据,每组数据包含五个 0~9 范围内的整数,分别求这 T 组数据中五个整数的权值。
【输⼊格式】
第⼀行⼀个整数 T (1<=T<=1000),表示数据组数。 接下来 T 行,每行 5 个 0~9 的整数,表示⼀组数据。
【输出格式】
输出 T 行,每行⼀个整数,表示每组数据中五个整数的权值。
【样例输⼊】
4
1 0 0 1 0
1 0 0 8 6
3 4 5 6 7
4 5 6 7 8
【样例输出】
2
-1
-1
0
#include<bits/stdc++.h>
using namespace std;
int a[5];
int n,mod;
int main(){cin>>n;while(n--){bool flag=false;cin>>a[0]>>a[1]>>a[2]>>a[3]>>a[4];mod=(a[0]+a[1]+a[2]+a[3]+a[4])%10;for(int i=0;i<5;i++){for(int j=i+1;j<5;j++){if((a[i]+a[j])%10==mod){cout<<mod<<endl;flag=true;break;}}}if(!flag)cout<<-1<<endl; }return 0;
}2.打地鼠
给定 n 个整数 a1, a2, …, an 和⼀个 d,你需要选出若⼲个整数,使得将这些整数从⼩到⼤排好序之 后,任意两个相邻的数之差都不⼩于给定的 d,问最多能选多少个数出来。
【输⼊格式】
第⼀行两个整数 n,d (1<=n<=10^5, 0<=d<=10^9),分别表示整数个数和相邻整数差的下界。 第⼆行 n 个整数 a1, a2, …, an (1<=ai<=10^9, 1<=i<=n),表示给定的 n 个整数。
【输出格式】
仅⼀行⼀个整数,表示答案。
【样例输⼊】
6 2
1 4 2 8 5 7
【样例输出】
3
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int a[N],n,d;
int main(){cin>>n>>d;if(n<2){cout<<0<<endl;return 0;} for(int i=0;i<n;i++){cin>>a[i];}sort(a,a+n);int cnt=1;for(int i=0,j=1;j<n;j++){if(a[j]-a[i]>=d){cnt++;i=j;}}if(cnt==1)cout<<0<<endl;else cout<<cnt<<endl;return 0;
}3.排队打饭
下课了,有 n 位同学陆续赶到⻝堂进行排队打饭,其中第 i 位同学的到达时间为 ai,打饭耗时为 ti, 等待时间上限为 bi,即如果其在第 ai+bi 秒的时刻仍然没有轮到他开始打饭,那么他将离开打饭队列 另寻吃饭的地⽅。问每位同学的开始打饭时间,或者指出其提前离开了队伍(如果这样则输出 -1)。
【输⼊格式】
第⼀行⼀个整数 n (1<=n<=10^5),表示来打饭的同学数量。 接下来 n 行,每行三个整数 ai,ti,bi (1<=ai,ti,bi<=10^9, 1<=i<=n),分别表示每位同学的到达时间、打 饭耗时、等待时间上限。 保证 a1<a2<…<an
【输出格式】
⼀行 n 个整数,表示每位同学的开始打饭时间或者 -1(如果该同学提前离开了队伍)。
【样例输⼊】
4
1 3 3
2 2 2
3 9 1
4 3 2
【样例输出】
1 4 -1 6
使用结构体存储学生的到来时间ai、打饭花费时间ti、等待时间bi、开始打饭时间st、打饭结束时间lt,第一个学生一定是能打到饭的,后面的学生需要判断等待是否超时:不超时的话,开始打饭时间就是max(ai, 前一个学生lv),并更新自己的打饭结束时间lv;超时的话,开始打饭时间就是-1,结束打饭时间取前一个学生的打饭结束时间。担心输入的学生数据不是按照到来的时间排序的,所以加了一次sort排序。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
struct stu{int ai,ti,bi,st,lt;
}a[N];
bool cmp(stu a,stu b){return a.ai<b.ai;
}
int main(){int n;cin>>n;for(int i=0;i<n;i++){cin>>a[i].ai>>a[i].ti>>a[i].bi;}sort(a,a+n,cmp);a[0].st=a[0].ai;a[0].lt=a[0].st+a[0].ti;cout<<a[0].st<<" ";for(int i=1;i<n;i++){if(a[i].ai+a[i].bi<a[i-1].lt){a[i].st=-1;a[i].lt=a[i-1].lt;}else{a[i].st=max(a[i].ai,a[i-1].lt);a[i].lt=a[i].st+a[i].ti;}cout<<a[i].st<<" ";}return 0;
}4.二叉排序树
给定⼀个 1~n 的排列 P,即⻓度为 n,且 1~n 中所有数字都恰好出现⼀次的序列。现在按顺序将排列中的元素⼀⼀插⼊到初始为空的⼆叉搜索树中(左⼩右⼤),问最后每个节点的⽗亲节点的元素是什么。特别地,根节点的⽗亲节点元素视为 0。
【输⼊格式】
第⼀行⼀个整数 n (1<=n<=10^5),表示排列 P 中的元素个数。 第⼆行 n 个整数 p1, p2, …, pn (1<=pi<=n, 1<=i<=n),表示给定的排列。
【输出格式】
⼀行 n 个整数,其中第 i 个整数 ai 表示元素 i 对应节点的⽗亲节点的元素。特别地,根节点的⽗亲节 点元素视为 0。
【样例输⼊】
5
2 3 5 1 4
【样例输出】
2 0 2 5 3
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
struct node{int parent,lchild=0,rchild=0;
}a[N];void locate(int root,int x){if(x>root){if(a[root].rchild)locate(a[root].rchild,x);else{a[root].rchild=x;a[x].parent=root;return;} }else{if(a[root].lchild)locate(a[root].lchild,x);else{a[root].lchild=x;a[x].parent=root;return;}}
}int main(){int n,root,x;cin>>n;cin>>root;a[root].parent=0;for(int i=2;i<=n;i++){cin>>x;locate(root,x);}for(int i=1;i<=n;i++){cout<<a[i].parent<<" ";}return 0;
}5.序列
给定⼀个⻓为 n 的序列 A,其中序列中的元素都是 0~9 之间的整数,对于⼀个⻓度同样为 n 整数序列 B,定义其权值为 |A_i-B_i| (1<=i<=n) 之和加上 (B_j-B_j+1)^2 (1<=j<n) 之和。求所有⻓为 n 的整数序 列中,权值最⼩的序列的权值是多少。
【输⼊格式】
第⼀行⼀个整数 n (1<=n<=10^5),表示序列 A 的⻓度。 第⼆行 n 个整数 a1, a2, …, an (0<=ai<=9, 1<=i<=n),表示序列 A 中的元素。 【
输出格式】
仅⼀行⼀个整数,表示答案。
【样例输⼊】
6
1 4 2 8 5 7
【样例输出】
11
dp[i][j]表示序列在第i个位置选择填入B_i=j的最小值。
状态转移方程:dp[i][j] = min(dp[i-1][k] + abs(j-now) + (j-k)^2)(for k=0; k<10; k++)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5,INF=0x3f3f3f3f3f;
int a[N],dp[N][12];
int n;int main(){cin>>n;for(int i=0;i<n;i++)cin>>a[i];memset(dp,0x3f,sizeof dp);for(int i=0;i<n;i++)dp[0][i]=abs(i-a[0]);for(int i=1;i<n;i++){for(int j=0;j<10;j++){for(int k=0;k<10;k++){dp[i][j]=min(dp[i][j],dp[i-1][k]+abs(a[i]-j)+(j-k)*(j-k));}}}int res=INF;for(int i=0;i<10;i++)res=min(res,dp[n-1][i]);cout<<res<<endl;return 0;
} 工研院2019
1.九键输入
实现九键输入,数字 2-9 对应九键中的 26 个字母,例如 2 代表 a,22 代表 b,222 代表 c,以此类推。0 表示空格,-表示停顿。若输入的字母按键相同,则中间应该用至少有一个“-”表示停顿。如输入 abc,则应是 2-22-222。现在保证输入仅仅含有数字 2-9,0,和停顿符“-”,并且可能存在无意义的停顿。要求输出最后的结果。
样例输入:255
输出:ak
样例输入:2-22—222
输出:abc
#include<bits/stdc++.h>
using namespace std;
char a[10][5] = {{'0', '0', '0', '0', '0'}, {'0', '0', '0', '0', '0'},{'A', 'B', 'C', '0', '0'},{'D', 'E', 'F', '0', '0'},{'G', 'H', 'I', '0', '0'},{'J', 'K', 'L', '0', '0'},{'M', 'N', 'O', '0', '0'},{'P', 'Q', 'R', 'S', '0'},{'T', 'U', 'V', '0', '0'},{'W', 'X', 'Y', 'Z', '0'}};
int main(){string str;getline(cin,str);int num=0;for(int i=0;i<str.length();i++){if(str[i]=='-')continue;if(str[i+1]!=str[i]){cout<<a[str[i]-'0'][num];num=0;}else{num++;}}return 0;
} 2.服务器维护
假设有编号从1-N的服务器,首先给出服务器个数,再给出一组服务器状态。
然后给出一次数字,表示修改状态次数,接下来输入为i,j,x,意思是使用x修改从i到j的服务器。
最后输出所有服务器状态
样例输入:
5
1 2 2 3 1
2
1 2 5
2 5 -1
输出:
6 6 1 2 0
//暴力
#include<bits/stdc++.h>
using namespace std;
int n,k;
int a[100];
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}cin>>k;while(k--){int x,y,z;cin>>x>>y>>z;for(int i=x;i<=y;i++){a[i]+=z;}}for(int i=1;i<=n;i++){cout<<a[i]<<" ";}return 0;
}
//前缀和与差分
#include<bits/stdc++.h>
using namespace std;
int n,k;
int a[100],b[100];
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];b[i]=a[i]-a[i-1];}cin>>k;while(k--){int x,y,z;cin>>x>>y>>z;b[x]+=z;b[y+1]-=z;}for(int i=1;i<=n;i++){a[i]=a[i-1]+b[i];cout<<a[i]<<" ";}return 0;
} 差分——前缀和逆运算:可用来求数组某一区间里的数加上同一个数值
设原数组为a1,a2...an,构造b数组使a数组为b数组的前缀和。即b数组为a数组的差分。
b1 = a1
b2 = a2 - a1
b3 = a3 - a2
...
bn = an - a(n-1)
若bi + c,则原数组ai ai+1 ... an都加上c。
同理若bj - c,则原数组aj,aj+1 ... an都会减去c。
故若想让ai到aj这个的数都加上c,只需bi + c,bj+1 - c。
3.通信代价
给定一个无向图,保证是一棵树,定义两个结点 ab 之间的通信代价为 ab 路径上的边的数目,节点 a 的通信代价为 a 到其他所有节点的通信代价之和。在一行中输出所有结点的通信代价。输入的一行数字表示节点数,下面每行各有两个数字a和b,表示节点a到节点b有直接路径。
样例输入:
4
1 2
2 3
2 4
输出:
5 3 5 5
#include<bits/stdc++.h>
using namespace std;
const int N=100;
int g[N][N];
int n,m;
void floyd(){for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){g[i][j]=min(g[i][j],g[i][k]+g[k][j]);}} }
}
int main(){cin>>n;m=n-1;memset(g,0x3f,sizeof g);for(int i=1;i<=n;i++){g[i][i]=0;}while(m--){int a,b;cin>>a>>b;g[a][b]=g[b][a]=1;}floyd();for(int i=1;i<=n;i++){int res=0;for(int j=1;j<=n;j++){res+=g[i][j];}cout<<res<<" ";}return 0;
}工研院2018
1.集合交并
输入两个集合,分别求其交集和并集中元素的个数,每个集合中可能存在相同的元素,而最终的交集和并集中应该不存在。
样例输入:
4 5
3 4 7 3
4 6 3 2 6
输出:
2 5
#include<bits/stdc++.h>
using namespace std;
set<int>A,B,C;
int n,m;
int main(){cin>>n>>m;while(n--){int x;cin>>x;A.insert(x);C.insert(x);}while(m--){int x;cin>>x;B.insert(x);C.insert(x);}int count=0;for(set<int>::iterator it=A.begin();it!=A.end();it++){if(B.find(*it)!=B.end()){count++;}}cout<<count<<" "<<C.size()<<endl;return 0;
} 2.约数求和
输入一个数n,输出前n个数的约数的和。(印象中有1s的时间限制,大数据集可能超时,比如100000000)。
样例输入:
7
输出:
41
#include<bits/stdc++.h>
using namespace std;
int count(int a){int sum=1+a;for(int i=2;i<a;i++){if(a%i==0)sum+=i;}return sum;
}
int main(){int n,sum=1;cin>>n;for(int i=2;i<=n;i++){sum+=count(i);}cout<<sum<<endl;return 0;
}3.交点
求线段交点,输入两组线段端点(整型),求其交点,不相交和无穷交点输出一句话就行,输出交点带小数的。
样例输入:
0 0 5 5
0 2 2 0
输出:
1 1
#include<bits/stdc++.h>
using namespace std;
int main(){double x1,y1,x2,y2,x3,y3,x4,y4;cin>>x1>>y1>>x2>>y2>>x3>>y3>>x4>>y4;double k1=(y2-y1)/(x2-x1),k2=(y4-y3)/(x4-x3),b1=y1-k1*x1,b2=y3-k2*x3;if(k1==k2)cout<<"平行或重合"<<endl;else{double x=(b2-b1)/(k1-k2),y=k1*x+b1;cout<<x<<" "<<y<<endl;}return 0;
} 计院2017
1.中位数
给定一个整数序列,求中位数。如果序列个数为奇数,中位数为升序的中间位置,如果是偶数,这位升序的中间两个数的平均值。输入包含多组测试数据,每一组第一行为n(n<104)表示这个序列的个数。接下来有n个整数k(0<k<231-1),输出这个序列的中位数。
输入1:
5
2 1 4 3 5
输出1:
3
输入2:
4
1 4 3 2
输出2:
3
#include<bits/stdc++.h>
using namespace std;
const int N=10010;
int a[N];int main(){int n;cin>>n;for(int i=0;i<n;i++){cin>>a[i];}sort(a,a+n);if(n%2==0){printf("%.2f\n",(a[n/2]+a[n/2-1])/2.0);}else{printf("%d\n",a[n/2]);}return 0;
}2.求校验位
给定一个9位数字的ISBN,求其校验位。ISBN格式为2-02-033598,校验位的计算方法如下:从左到右依次将各位数字乘10,9,8,……,2,求出其和S,作模运算得M=S mod 11。若11-M在1和9之间,校验位即为该数字;若11-M等于10,校验位为X;11-M等于11,校验位为0。输出添加校验位的ISBN,如2-02-033598-0。
输入1:
2-02-033598
输出1:
2-02-033598-0
输入2:
7-309-04547
输出2:
7-309-04547-5
#include<bits/stdc++.h>
using namespace std;int main(){int j=10,sum=0;char s[15];cin>>s;for(int i=0;i<11;i++){if(s[i]!='_'){sum+=(s[i]-'0')*j;j--;}}sum=11-(sum%11);cout<<s<<"_";if(sum<=9) cout<<sum<<endl;else if(sum==10) cout<<"X"<<endl;else cout<<"0"<<endl;return 0;
}3.最小生成树
一个无向图,顶点为N个,顶点编号为1~N,其中M条边已给定,现在要从K条备选边中选出若干条,使得整个图连通,且选出的边权值和最小。
输入
第一行输入三个整数N(N<100), M, K,接下来一行为K个整数表示备选边的编号。然后是是M行,每行三个数字:u,v,d(0<d<10000)表示结点u和结点v的边,权值为d,编号按照输入输入顺序依次为1~M。
输出
如果输入有解则输出选出的边的权值和否则输出-1
题意不清,参Acwing的题859,Kruskal算法求最小生成树
#include<bits/stdc++.h>
using namespace std;
const int N=100010,M=200010;
int p[N];
int n,m;
struct edge{int u,v,w;
}e[M];
bool cmp(edge a,edge b){return a.w<b.w;
}
int find(int x){//并查集 if(p[x]!=x)p[x]=find(p[x]);return p[x];
}
void kruskal(){sort(e,e+m,cmp);int cnt=0,res=0;for(int i=0;i<m;i++){int u=e[i].u,v=e[i].v,w=e[i].w;if(find(u)!=find(v)){p[find(u)]=find(v);cnt++;res+=w;}}if(cnt==n-1)cout<<res<<endl;else puts("impossible");
}
int main(){cin>>n>>m;for(int i=0;i<n;i++){p[i]=i;}for(int i=0;i<m;i++){int u,v,w;cin>>u>>v>>w;e[i]={u,v,w};}kruskal();return 0;
}