注:代码是本菜鸡自己个儿写的,没有找到参考答案,欢迎各位大佬批评指正.
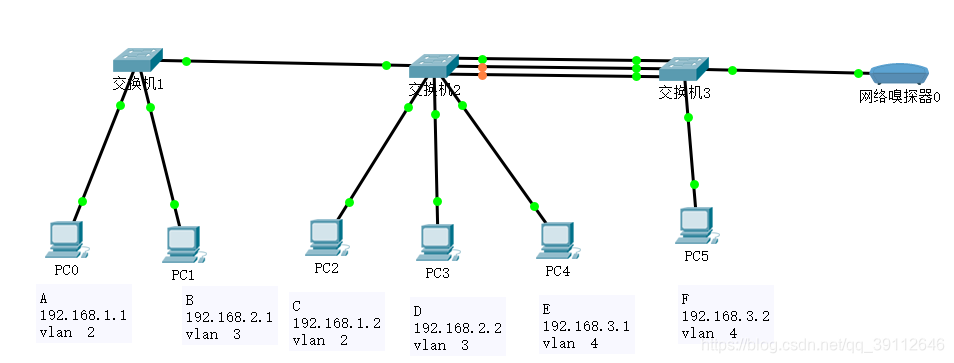
题目如下图所示(图片来源网上):

第1题
该题主要考察拓扑排序.其实该算法有通用模板,但我写的时候没有意识到使用,代码不是很规范.
#define _CRT_SECURE_NO_WARNINGS#include <iostream>
#include <vector>
#include <queue>using namespace std;
const int maxn = 110;vector<int> after[maxn];
vector<int> path;
queue<int> q;
int n;
bool vis[maxn] = { false }, pre[maxn] = { false };int main() {scanf("%d", &n);char c;int a, b;scanf("%c", &c);while (c ==',') {scanf(" [%d, %d]", &a, &b);after[b].push_back(a);pre[a] = true;//有前置结点scanf("%c", &c);}//找到入度为0的结点(开始节点)for (int i = 0; i < n; i++) {if (pre[i] == false) {q.push(i);}}//BFS遍历int node;while (q.size()>0) {//如果队列不为空node = q.front();q.pop();if (vis[node] == false) {path.push_back(node);vis[node] = true;for (int i = 0; i < after[node].size(); i++) {if (vis[after[node][i]] == false) {q.push(after[node][i]);}}} }for (int i = 0; i < path.size(); i++) {printf("%d", path[i]);if (i == path.size() - 1) printf("\n");else printf(", ");}return 0;
}
测试用例1
In:
4, [1, 0], [2, 0], [3, 1], [3, 2]
Out:
0, 1, 2, 3测试用例2
In:
2, [0, 1]
Out:
1, 0测试用例3
In:
4, [0, 1], [2, 1], [3, 1]
Out:
1, 0, 2, 3测试用例4
In:
5, [1, 0], [2, 0], [3, 0], [4, 2], [4, 3]
Out:
0, 1, 2, 3, 4测试用例5
In:
6, [3, 0], [3, 1], [3, 2], [4, 3], [5, 3]
Out:
0, 1, 2, 3, 4, 5
第2题
- 该题主要考察动态规划.
- 对于题目给出的测试用例,输入没有给出矩阵的行数和列数,而是直接输入矩阵.由于所给矩阵并不一定是方阵(即行数和列数相等),我这个菜鸡不会判断它的输入何时结束,只能偷偷加了两个输入条件,即先输入矩阵的行数和列数,再输入这个矩阵.
刚开始时我写不出来动态规划解法,只能暴力求解:
#define _CRT_SECURE_NO_WARNINGS#include <iostream>
#include <cstring>
#include <algorithm>
//#include <string>using namespace std;
const int maxn = 110;int G[maxn][maxn], res[maxn][maxn];
int m, n;int main() {scanf("%d %d", &m, &n);//输入矩阵的行数和列数int len = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {scanf("%d", &G[i][j]);//res[i][j] = G[i][j];if (G[i][j] == 1) len = 1;}}if (len == 0) {printf("0\n");return 0;}int maxL = len;//复杂度较高while (len <= min(m, n)&&maxL==len) {for (int i = 0; i < m - len; i++) {for (int j = 0; j < n - len; j++) {if (G[i][j] != 0) {if (G[i][j] <= G[i + 1][j] && G[i][j] <= G[i][j + 1] && G[i][j] <= G[i + 1][j + 1]) {G[i][j]++;maxL = max(maxL, G[i][j]);}}}}len++;}printf("%d\n", maxL);return 0;
}
后来参考了一下网上类似题目的代码,遂将该题的代码更改如下:
#define _CRT_SECURE_NO_WARNINGS#include <iostream>
#include <cstring>
#include <algorithm>
//#include <string>using namespace std;
const int maxn = 110;int G[maxn][maxn], res[maxn][maxn];
int m, n;int main() {scanf("%d %d", &m, &n);//输入矩阵的行数和列数int len = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {scanf("%d", &G[i][j]);//res[i][j] = G[i][j];if (G[i][j] == 1) len = 1;}}if (len == 0) {printf("0\n");return 0;}int maxL = len;//动态规划for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (G[i][j] > 0) {G[i][j] = min(min(G[i - 1][j], G[i][j - 1]),G[i-1][j-1]);G[i][j]++;maxL = max(maxL, G[i][j]);}}}printf("%d\n", maxL);return 0;
}
测试用例1
In:
4 5
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Out:
2测试用例2
In:
2 2
0 0
0 0
Out:
0测试用例3
In:
2 3
1 1 1
1 1 1
Out:
2测试用例4
In:
3 3
1 1 1
1 1 1
1 1 1
Out:
3
第3题
emm,这个题俺不知道复杂度较小的代码咋写,只能暴力求解了:
#define _CRT_SECURE_NO_WARNINGS#include <iostream>
#include <vector>
#include <algorithm>using namespace std;
const int maxn = 110;struct Node
{int v, val;Node(int _v, int _val) :v(_v), val(_val) {}
};int n, m, father[maxn];
bool vis[maxn], black[maxn] = { false };
vector<Node> G[maxn];//邻接表(无向)
int ans;void DFS(int v,int len) {vis[v] = true;for (int i = 0; i < G[v].size(); i++) {int u = G[v][i].v;if (vis[u] == false) {if (black[u] == true) {ans+=(len + G[v][i].val);}DFS(u, len + G[v][i].val);}}
}int main() {scanf("%d %d", &n, &m);int val;for (int i = 1; i < n; i++) {scanf("%d", &father[i]);}for (int i = 1; i < n; i++) {scanf("%d", &val);G[i].push_back(Node(father[i], val));G[father[i]].push_back(Node(i,val));}int t, c;for (int i = 0; i < m; i++) {scanf("%d %d", &t, &c);if (t == 1) black[c] = true;else if (t == 2) {fill(vis, vis + maxn, false);ans = 0;DFS(c,0);printf("%d\n", ans);}}return 0;
}
测试用例1
In:
4 5
0 1 2
2 1 3
2 2
1 3
2 2
2 3
2 1
Out:
0
3
0
4测试用例2
In:
7 8
0 0 0 1 1 2
2 1 3 1 6 3
2 5
1 4
1 5
2 5
1 6
1 0
2 0
2 1
Out:
0
7
15
15