Log-Euclidean测度是黎曼流形上一种常用的测度,Log-Euclidean测度形式简单,方便计算,因此在基于黎曼流形的算法中被广泛应用。
1.什么是测度
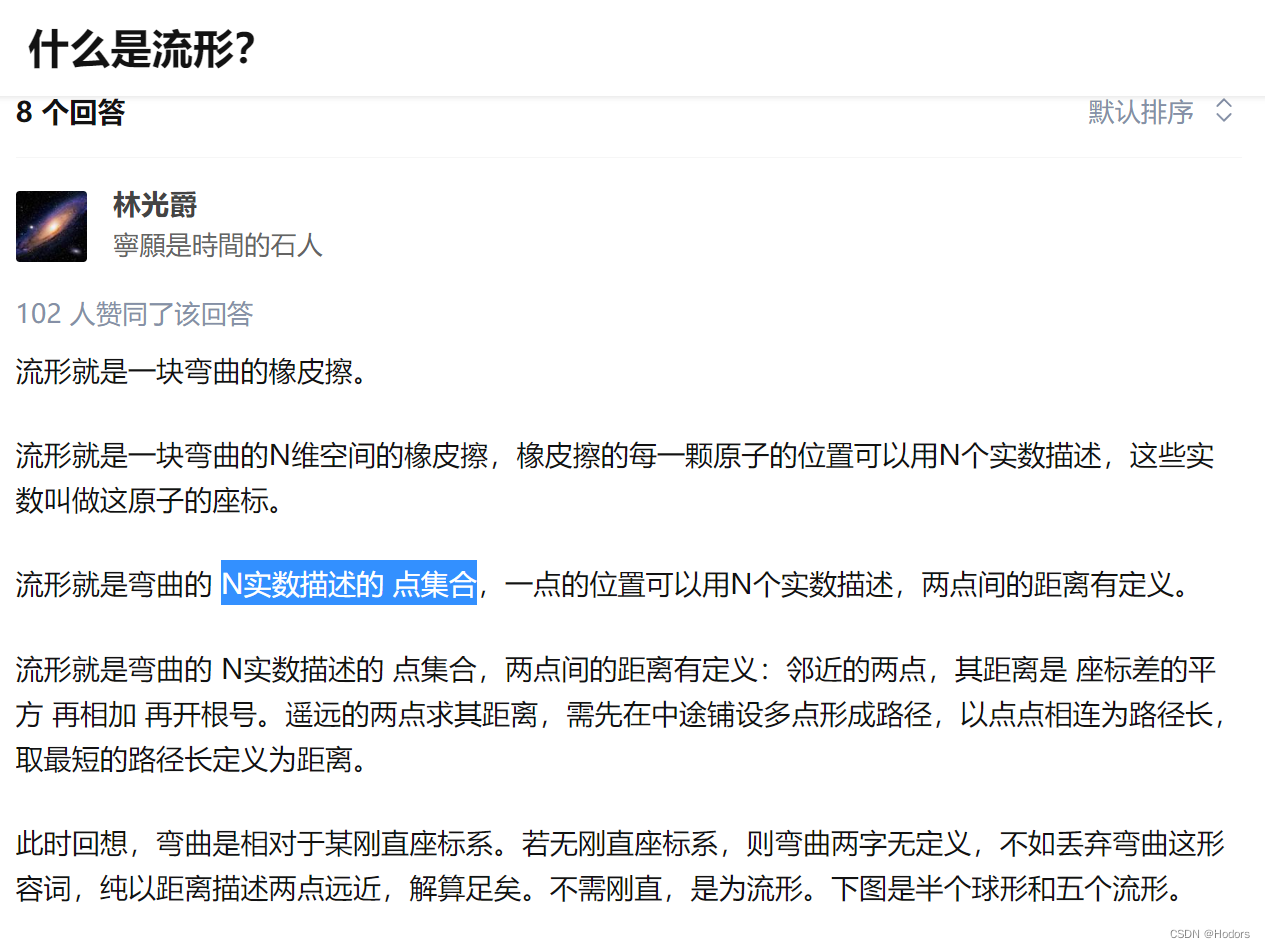
在黎曼流形上,要衡量两个点之间的距离,不能像欧式空间那样直接用范数计算,所以引入了测地距离作为流形上两个点之间距离的度量。
测地距离:流形上两个点之间的最短测地线的长度。
测地线:流形上两个点之间最短的曲线。
黎曼测度:黎曼流形上某一点的切空间上定义的内积的集合。
黎曼测度的性质:黎曼流形上某一点的切空间上某一切向量的范数等于这个切向量对应的测地线的长度。
2.Log-Euclidean测度
SPD流形:由对称正定矩阵(PSD matrix)组成的流形。记为,表示由nxn SPD矩阵组成的流形。
,X和Y之间的Log-Euclidean测度为:
3.Log-Euclidean测度的性质
与其他常用的黎曼测度相比,Log-Euclidean测度不是仿射不变的,仿射不变指的是黎曼流形上两个点之间的测度值在仿射之后保持不变,即。
此外,Log-Euclidean测度并没有完全真实地反映了黎曼流形上两个点之间的几何关系(即测地距离)。