目录

一、中短期预测

1、灰色预测法

①适用范围

②模型实现

 2、回归分析

①适用范围

②模型实现

 3、时间序列分析

①自适应滤波法

②指数平滑法

③移动平均法

4、微分方程

二、长期预测

1、神经网络预测

2、logistic模型

①模型介绍

②模型分析及代码

一、中短期预测

1、灰色预测法

灰色预测模型 （ Gray Forecast Model ）是通过少量的、不完全的信息，建立数学模型并做出预测的一种预测方法。当我们应用运筹学的思想方法解决实际问题，制定发展战略和政策、进行重大问题的决策时，都必须对未来进行科学的预测 。预测是根据客观事物的过去和现在的发展规律，借助于科学的方法对其未来的发展趋势和状况进行描述和分析，并形成科学的假设和判断。

①适用范围

适用范围：该模型使用的不是原始数据的序列，而是生成的数据序列。核心体系是Grey Model，即对原始数据作累加生成（或其他处理生成）得到近似的指数规律再进行建模的方法。

优点：在处理较少的特征值数据，不需要数据的样本空间足够大，就能解决历史数据少、序列的完整性以及可靠性低的问题，能将无规律的原始数据进行生成得到规律较强的生成序列。

缺点：只适用于中短期的预测，只适合近似于指数增长的预测。

②模型实现

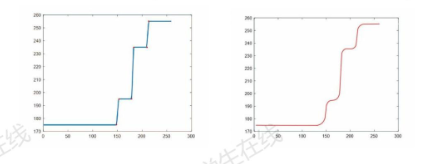
GM(1,1)模型适用 于具有较强指数规律的序列，只能描述单调的变化过程，而 Verhulst 模型则适用于非单 调的摆动发展序列或具有饱和状态的 S 形序列。下面对比一下两种方法：

用matlab语言采用Verhulst模型预测

clc,clear
x1=[4.93 5.33 5.87 6.35 6.63 7.15 7.37 7.39 7.81 8.35 9.39 10.59 10.94 10.44];
n=length(x1);
nian=1990:2003;
plot(nian,x1,'o-');
x0=diff(x1);
x0=[x1(1),x0]
for i=2:nz1(i)=0.5*(x1(i)+x1(i-1));
end
z1
B=[-z1(2:end)',z1(2:end)'.^2]
Y=x0(2:end)'
abhat=B\Y %估计参数 a,b 的值
x=dsolve('Dx+a*x=b*x^2','x(0)=x0'); %求解常微分方程
x=subs(x,{'a','b','x0'},{abhat(1),abhat(2),x1(1)}); %代入参数值
yuce=subs(x,'t',0:14) %计算预测值
digits(6); x=vpa(x) %显示微分方程的解，为了提高计算精度，把该语句放在计算预测值之后，或者不使用该语句
yuce(16)=yuce(15);
x1_all=[x1,9.92,10.71];
epsilon=x1_all-yuce %计算残差
delta=abs(epsilon./x1_all) %计算相对误差
delta_mean=mean(delta) %计算平均相对误差
x1_all_0=x1_all-x1_all(1); %数据列的始点零化像
yuce_0=yuce-yuce(1); %数据列的始点零化像
s0=abs(sum(x1_all_0(1:end-1))+0.5*x1_all_0(end));
s1=abs(sum(yuce_0(1:end-1))+0.5*yuce_0(end));
tt=yuce_0-x1_all_0;
s1_s0=abs(sum(tt(1:end-1))+0.5*tt(end));
absdegree=(1+s0+s1)/(1+s0+s1+s1_s0) %计算灰色绝对关联度
c=std(epsilon,1)/std(x1_all,1) %计算标准差比值

参考文章：http://t.csdn.cn/OIMNK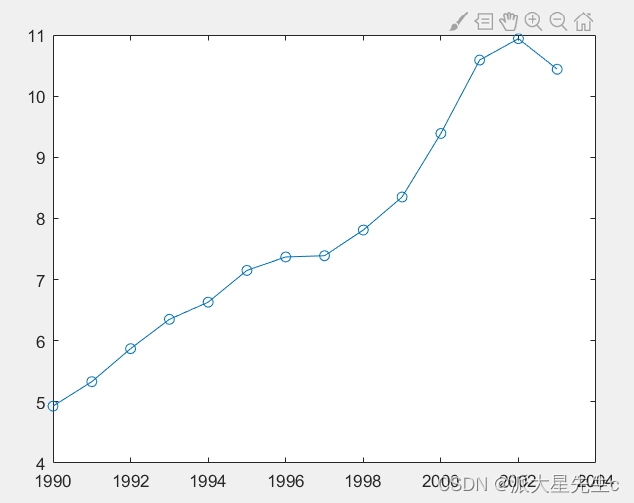参考文章：http://t.csdn.cn/OIMNK

用python语言采用GM(1,1）微分方程预测

import numpy as np
import mathhistory_data = [4.93, 5.33, 5.87, 6.35, 6.63, 7.15, 7.37, 7.39, 7.81, 8.35,9.39, 10.59, 10.94, 10.44]
n = len(history_data)
X0 = np.array(history_data)# 累加生成
history_data_agg = [sum(history_data[0:i + 1]) for i in range(n)]
X1 = np.array(history_data_agg)# 计算数据矩阵B和数据向量Y
B = np.zeros([n - 1, 2])
Y = np.zeros([n - 1, 1])
for i in range(0, n - 1):B[i][0] = -0.5 * (X1[i] + X1[i + 1])B[i][1] = 1Y[i][0] = X0[i + 1]# 计算GM(1,1)微分方程的参数a和u
# A = np.zeros([2,1])
A = np.linalg.inv(B.T.dot(B)).dot(B.T).dot(Y)
a = A[0][0]
u = A[1][0]# 建立灰色预测模型
XX0 = np.zeros(n)
XX0[0] = X0[0]
for i in range(1, n):XX0[i] = (X0[0] - u / a) * (1 - math.exp(a)) * math.exp(-a * (i));# 模型精度的后验差检验
e = 0  # 求残差平均值
for i in range(0, n):e += (X0[i] - XX0[i])
e /= n# 求历史数据平均值
aver = 0;
for i in range(0, n):aver += X0[i]
aver /= n# 求历史数据方差
s12 = 0;
for i in range(0, n):s12 += (X0[i] - aver) ** 2;
s12 /= n# 求残差方差
s22 = 0;
for i in range(0, n):s22 += ((X0[i] - XX0[i]) - e) ** 2;
s22 /= n# 求后验差比值
C = s22 / s12# 求小误差概率
cout = 0
for i in range(0, n):if abs((X0[i] - XX0[i]) - e) < 0.6754 * math.sqrt(s12):cout = cout + 1else:cout = cout
P = cout / nif (C < 0.35 and P > 0.95):# 预测精度为一级m = 2  # 请输入需要预测的年数# print('往后m各年负荷为：')f = np.zeros(m)for i in range(0, m):f[i] = (X0[0] - u / a) * (1 - math.exp(a)) * math.exp(-a * (i + n))print(f[i])
else:print('灰色预测法不适用')

 2、回归分析

①适用范围

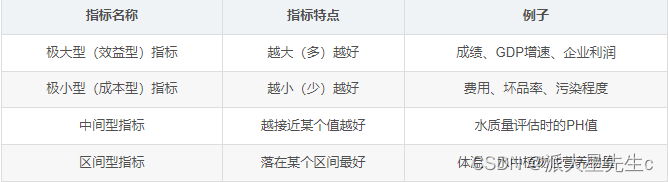
     回归分析是研究变量之间因果关系的一种统计模型；因变量就是结果，自变量就是原因；基于结果变量（因变量）的种类，回归分析可分为：线性回归（因变量为连续变量）、logistic回归（因变量为分类变量）、柏松回归（因变量为计数变量）；这三种回归模型中自变量则可以是任意类型的变量。

  有的自变量对因变量的影响不是很大，且自变量之间可能存在多重共线性（即可能不完全独立），通过建立逐步回归分析，进行X因子筛选。

比如：收入水平于受教育程度、所在行业、工作年限、工作种类的关系；公路客运量与人口增长量、私家车保有量、国民生产总值、国民收入等因素的关系。

②模型实现

几种回归分析的matlab代码如下

非线性回归

%% 非线性回归
clc, clearx0 = [1  8.55  470  300  102  3.79  285  80  103  4.82  470  300  1204  0.02  470  300  1205  2.75  470    80   106 14.39  100  190  107  2.54   100   80   658  4.35   470  190  659    13  100  300  5410  8.5  100  300  12011  0.05  100  80  12012  11.32  285  300  1013  3.13  285  190  120];x = x0(:, 3:5);
y = x0(:, 2);% 参数的初始预估值
beta = [0.1, 0.05, 0.02, 1, 2]';[betahat, r, j] = nlinfit(x, y, @func, beta);
betaci = nlparci(betahat, r, 'jacobian', j);
% 回归系数以及置信区间
betaa = [betahat, betaci];
% y的预测值以及置信区间半径
[yhat, delta] = nlpredci(@func, x, betahat, r, 'jacobian', j);% 绘制交互式画面
nlintool(x, y, 'func', beta)

 逐步回归模型

%% 逐步回归模型
clc, clearx0 = [1  8.55  470  300  102  3.79  285  80  103  4.82  470  300  1204  0.02  470  300  1205  2.75  470    80   106 14.39  100  190  107  2.54   100   80   658  4.35   470  190  659    13  100  300  5410  8.5  100  300  12011  0.05  100  80  12012  11.32  285  300  1013  3.13  285  190  120];x = x0(:, 3:5);
y = x0(:, 2);stepwise(x, y)

 一元多项回归模型

%% 一元多项式回归模型
% 选取 y = a2*x^2 + a1*x + a0
clc, clearx0 = 17: 2: 29;
y0 = [20.48, 25.13, 26.15, 30.0, 26.1, 20.3, 19.35];[p, s] = polyfit(x0, y0, 2);  % 2表示阶数
p                                              % p返回a2，a1，a0三个参数% 求polyfit所得的回归多项式在x0处的预测值Y
%及预测值的显著性为1-alpha的置信区间DELTA；
%alpha缺省时为0.05。它假设polyfit函数数据输入的误差是独立正态的，并且方差为常数
[y, delta] = polyconf(p, x0, s);   % delta为置信区间半径polytool(x0, y0, 2)

 

 多元二项式回归

%% 多元二项式回归
% rstool(x, y, model, alpha) 
% model有四种：线性，纯二次，交叉，完全二次
clc, clearx1 = [120 140 190 130 155 175 125 145 180 150]';
x2 = [100 110    90 150 210 150 250 270 300 250]';
y   = [102  100 120  77 46  93  26  69  65  85]';x = [x1 x2];
rstool(x, y, 'purequadratic')

一元（多元）线性回归

%% 一元（多元）线性回归%x = input('输入需要预测的一组数据:(如[0.10 0.11 0.12 ...)\n');
% 测试用例：
x1 = [0.1:0.01:0.18]';
%y = input('输入需要预测的一组数据:(如[0.10 0.11 0.12 ...)\n');
% 测试用例：
y = [42, 41.5, 45.0, 45.5, 45.0, 47.5, 49.0, 55.0, 50.0]';
plot(x1, y, '+')  % 观察是否近似为线性模型x = [ones(9, 1), x1];
[b, bint, r, rint, stats] = regress(y, x);
b                         %回归系数估计值
bint                    %回归系数置信区间
stats                   %检验回归系统的统计量：复判定系数等
rcoplot(r, rint)  %残差向量与残差置信区间
%--根据rcoplot的绘制结果，剔除异常点之后重新生成回归系统--%

 

偏最小二乘回归（PLS）   python代码

import numpy as npx1 = [191, 189, 193, 162, 189, 182, 211, 167, 176, 154, 169, 166, 154, 247, 193, 202, 176, 157, 156, 138]
x2 = [36, 37, 38, 35, 35, 36, 38, 34, 31, 33, 34, 33, 34, 46, 36, 37, 37, 32, 33, 33]
x3 = [50, 52, 58, 62, 46, 56, 56, 60, 74, 56, 50, 52, 64, 50, 46, 62, 54, 52, 54, 68]
y1 = [5, 2, 12, 12, 13, 4, 8, 6, 15, 17, 17, 13, 14, 1, 6, 12, 4, 11, 15, 2]
y2 = [162, 110, 101, 105, 155, 101, 101, 125, 200, 251, 120, 210, 215, 50, 70, 210, 60, 230, 225, 110]
y3 = [60, 60, 101, 37, 58, 42, 38, 40, 40, 250, 38, 115, 105, 50, 31, 120, 25, 80, 73, 43]
# -----数据读取
data_raw = np.array([x1, x2, x3, y1, y2, y3])
data_raw = data_raw.T  # 输入原始数据，行数为样本数，列数为特征数
# -----数据标准化
num = np.size(data_raw, 0)  # 样本个数
mu = np.mean(data_raw, axis=0)  # 按列求均值
sig = (np.std(data_raw, axis=0))  # 按列求标准差
data = (data_raw - mu) / sig  # 标准化，按列减去均值除以标准差
# -----提取自变量和因变量数据
n = 3  # 自变量个数
m = 3  # 因变量个数
x0 = data_raw[:, 0:n]  # 原始的自变量数据
y0 = data_raw[:, n:n + m]  # 原始的变量数据
e0 = data[:, 0:n]  # 标准化后的自变量数据
f0 = data[:, n:n + m]  # 标准化后的因变量数据
# -----相关矩阵初始化
chg = np.eye(n)  # w到w*变换矩阵的初始化
w = np.empty((n, 0))  # 初始化投影轴矩阵
w_star = np.empty((n, 0))  # w*矩阵初始化
t = np.empty((num, 0))  # 得分矩阵初始化
ss = np.empty(0)  # 或者ss=[]，误差平方和初始化
press = []  # 预测误差平方和初始化
Q_h2 = np.zeros(n)  # 有效性判断条件值初始化
# -----求解主成分
for i in range(n):  # 主成分的总个数小于等于自变量个数# -----求解自变量的最大投影w和第一主成分tmatrix = e0.T @ f0 @ f0.T @ e0  # 构造矩阵E'FF'Eval, vec = np.linalg.eig(matrix)  # 计算特征值和特征向量index = np.argsort(val)[::-1]  # 获取特征值从大到小排序前的索引val_sort = val[index]  # 特征值由大到小排序vec_sort = vec[:, index]  # 特征向量按照特征值的顺序排列w = np.append(w, vec_sort[:, 0][:, np.newaxis], axis=1)  # 储存最大特征向量w_star = np.append(w_star, chg @ w[:, i][:, np.newaxis], axis=1)  # 计算 w*的取值t = np.append(t, e0 @ w[:, i][:, np.newaxis], axis=1)  # 计算投影alpha = e0.T @ t[:, i][:, np.newaxis] / (t[:, i] @ t[:, i])  # 计算自变量和主成分之间的回归系数chg = chg @ (np.eye(n) - (w[:, i][:, np.newaxis] @ alpha.T))  # 计算 w 到 w*的变换矩阵e1 = e0 - t[:, i][:, np.newaxis] @ alpha.T  # 计算残差矩阵e0 = e1  # 更新残差矩阵# -----求解误差平方和ssbeta = np.linalg.pinv(t) @ f0  # 求回归方程的系数，数据标准化，没有常数项res = np.array(f0 - t @ beta)  # 求残差ss = np.append(ss, np.sum(res ** 2))  # 残差平方和# -----求解残差平方和presspress_i = []  # 初始化误差平方和矩阵for j in range(num):t_inter = t[:, 0:i + 1]f_inter = f0t_inter_del = t_inter[j, :]  # 把舍去的第 j 个样本点保存起来,自变量f_inter_del = f_inter[j, :]  # 把舍去的第 j 个样本点保存起来，因变量t_inter = np.delete(t_inter, j, axis=0)  # 删除自变量第 j 个观测值f_inter = np.delete(f_inter, j, axis=0)  # 删除因变量第 j 个观测值t_inter = np.append(t_inter, np.ones((num - 1, 1)), axis=1)beta1 = np.linalg.pinv(t_inter) @ f_inter  # 求回归分析的系数,这里带有常数项res = f_inter_del - t_inter_del[:, np.newaxis].T @ beta1[0:len(beta1) - 1, :] - beta1[len(beta1) - 1, :]  # 计算残差res = np.array(res)press_i.append(np.sum(res ** 2))  # 残差平方和，并存储press.append(np.sum(press_i))  # 预测误差平方和# -----交叉有效性检验，判断主成分是否满足条件Q_h2[0] = 1if i > 0:Q_h2[i] = 1 - press[i] / ss[i - 1]if Q_h2[i] < 0.0975:print('提出的成分个数 r=', i + 1)break
# -----根据主成分t计算回归方程的系数
beta_Y_t = np.linalg.pinv(t) @ f0  # 求Y*关于t的回归系数
beta_Y_X = w_star @ beta_Y_t  # 求Y*关于X*的回归系数
mu_x = mu[0:n]  # 提取自变量的均值
mu_y = mu[n:n + m]  # 提取因变量的均值
sig_x = sig[0:n]  # 提取自变量的标准差
sig_y = sig[n:n + m]  # 提取因变量的标准差
ch0 = mu_y - mu_x[:, np.newaxis].T / sig_x[:, np.newaxis].T @ beta_Y_X * sig_y[:, np.newaxis].T  # 算原始数据回归方程的常数项
beta_target = np.empty((n, 0))  # 回归方程的系数矩阵初始化
for i in range(m):a = beta_Y_X[:, i][:, np.newaxis] / sig_x[:, np.newaxis] * sig_y[i]  # 计算原始数据回归方程的系数beta_target = np.append(beta_target, a, axis=1)
target = np.concatenate([ch0, beta_target], axis=0)  # 回归方程的系数，每一列是一个方程，每一列的第一个数是常数项
print(target)

程序结果为：

提出的成分个数 r= 2
[[ 4.70197312e+01  6.12567103e+02  1.83984900e+02]
 [-1.66507920e-02 -3.50879763e-01 -1.25347701e-01]
 [-8.23702347e-01 -1.02476743e+01 -2.49692623e+00]
 [-9.69133092e-02 -7.41217596e-01 -5.18112643e-02]]

 3、时间序列分析

①自适应滤波法

%% 自适应滤波法
clc, clearyt = 0.1:0.1:1;
m = length(yt);
k = 0.9;          % 学习常数
N = 2;            % 权数个数
Terr = 10000;
w = ones(1,N) / N;
while abs(Terr)>0.00001Terr = [];for j = N+1:m-1yhat(j) = w*yt(j-1:-1:j-N)';err = yt(j) - yhat(j);Terr = [Terr, abs(Terr)];w = w + 2*k*err*yt(j-1:-1:j-N);endTerr = max(Terr);
end

②指数平滑法

二次指数平滑法

%% 二次指数平滑法
clc, clearyt = [676 825 774 716 940 1159 1384 1524 1668 1688 1958 2031 2234 2566 2820 3006 3093 3277 3514 3770 4107]';
n = length(yt);
alpha = 0.3;
st1(1) = yt(1); st2(1) = yt(1);  % 初始值选实际初始值
for i = 2:nst1(i) = alpha*yt(i) + (1-alpha)*st1(i-1);st2(i) = alpha*st1(i) + (1-alpha)*st2(i-1);
endat = 2*st1 - st2;
bt = alpha/(1-alpha)*(st1-st2);
yhat = at + bt;
y_predict = alpha*yt(n) + (1-alpha)*yhat(n);x = 1965:1985;
plot(x, yt, '*', x, yhat);

③移动平均法

1、加权平均移动法

%% 加权移动平均法
clc ,cleary = [6.35 6.20 6.22 6.66 7.15 7.89 8.72 8.94 9.28 9.80];
w = [1/6; 2/6; 3/6];   % 各加权项的权重
m = length(y);
n = 3;                 % 移动平均的项数
for i = 1:m-n+1yhat(i) = y(i:i+n-1)*w;
end
err = abs(y(n+1:m)-yhat(1:end-1))./y(n+1:m);  % 计算相对误差(最开始的三项数据是没有相对误差的)
T_err = 1 - sum(yhat(1:end-1))/sum(y(n+1:m)); % 计算总的相对误差
y_predict = yhat(end) / (1-T_err);            % 用总的相对误差修正预测值

2、趋势移动平均法

%% 趋势移动平均法
% 在一次移动平均的基础上再做一次移动平均
clc, cleary = [676 825 774 716 940 1159 1384 1524 1668 1688 1958 2031 2234 2566 2820 3006 3093 3277 3514 3770 4107];% 第一次移动平均
m1 = length(y);
n = 6;    % 移动平均的项数
for i = 1:m1-n+1yhat1(i) = sum(y(i:i+n-1))/n;
end% 第二次移动平均
m2 = length(yhat1);
for i = 1:m2-n+1yhat2(i) = sum(yhat1(i:i+n-1))/n;
endplot(1:m1, y, '*');
% 计算平滑系数
at = 2*yhat1(end) - yhat2(end);
bt = 2*(yhat1(end)-yhat2(end)) / (n-1);% 预测后两个数值
y_predict1 = at + bt;
y_predict2 = at + 2*bt;

3、简单移动平均法

%% 简单移动平均法
clc, cleary = [533.8 574.6 606.9 649.8 705.1 772.0 816.4 892.7 963.9 1015.1 1102.7];
m = length(y);
n = [4,5];    % n位移动平均的项数，选取4和5分别做一次运算
for i = 1:length(n)for j = 1:m-n(i)+1yhat{i}(j) = sum(y(j:j+n(i)-1))/n(i);endy_predict(i) = yhat{i}(end);  % 预测值s(i) = sqrt(mean( (y(n(i)+1:m) - yhat{i}(1:end-1)).^2 )); % 预测的标准误差
end

4、微分方程

参考之前的文章：《MATLAB--微分方程》

http://t.csdn.cn/ub34W

二、长期预测

1、神经网络预测

参考之前的文章：

http://t.csdn.cn/zw7ou


 

以及参考深度学习专栏

搭建神经网络进行一些模型的预测

2、logistic模型

①模型介绍

• 优点：计算代价不高，易于理解和实现。
• 缺点：容易欠拟合，分类精度可能不高。
• 使用数据类型：数值型和标称型数据。

②模型分析及代码

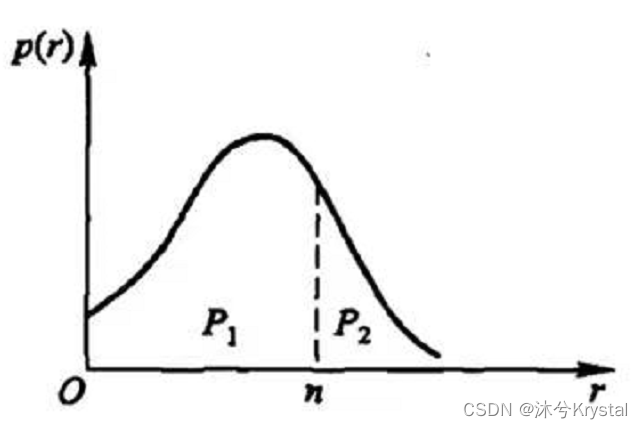
荷兰生物学家 Verhaust 于 1838 年提出了以昆虫数量为基础的 Logistic 人口增长模型。这个模型假设增长率 r 是人口的函数，它随着 x 的增加而减少。由 r(x)的表达式可知，当 x=𝑥𝑚时， r=0。其中， 𝑥𝑚表示自然资源条件能容纳的最大人口数。 Logistic 模型综合考虑了环境等因素对人口增长产生的影响，因此也是一种被广泛应用的效果较好的模型。\n\n设时刻 t 时人口为 x(t)，环境允许的最大人口数量为𝑥𝑚，人口净增长率随人口数量的增加而线性减少，即：

 体现了环境和资源对人口增长的阻滞作用，显然 x 越大，该因子越大，说明随着人口数量 x 的增加，阻滞作用越来越大。\n\n由此建立 Logistic 人口模型的微分方程:

根据附件给出的 1997-2016 年每年的人口数量，运用 MATLAB 进行编程处理，可以比较 1997-2016 年实际人口与拟合线的拟合程度，由图 1.1 可见， Logistic 模型对过去 20 年人口数量拟合效果较好。通过拟合，得到了待求参数 r=0.0394， 𝑥𝑚=1.5501× 105。因为以 1997 年为起算点，所以𝑥0=1.23626× 105。 则 Logistic 人口模型函数方程为:

 

 

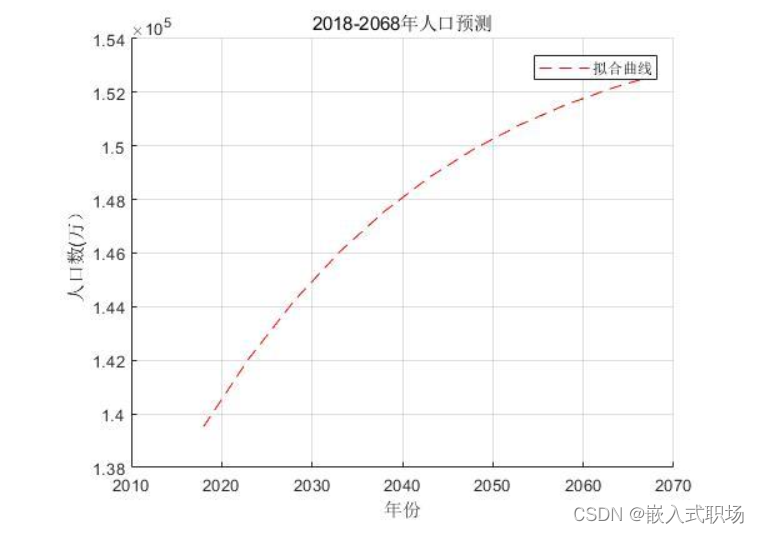
 由 MATLAB 拟合出来的 Logistic 函数进行 2018-2068 年的人口预测， 人口数缓慢上升，经过 50 年人口增长了 13120 万人， Logistic 模型也求得在资源和环境的限制下， 无论过了多少年的人口不会超过 155010万人。在考虑资源和环境的阻滞作用随着人口增多也会越来越大的情况下，上述结果与实际是相符合的。

clc,clear,
t=1997:1:2016;
x=[123626 124761 125786 126743 127627 128453 129227 129988 130756 131448
132129 132802 133450 134091 134735 135404 136072 136782 137462 138271];
x1=[123626 124761 125786 126743 127627 128453 129227 129988 130756 131448
132129 132802 133450 134091 134735 135404 136072 136782 137462];
x2=[124761 125786 126743 127627 128453 129227 129988 130756 131448 132129
132802 133450 134091 134735 135404 136072 136782 137462 138271];
dx=(x2-x1)./x2;a=polyfit(x2,dx,1);
r=a(2),xm=-r/a(1)
x0=123626;
f=inline('xm./(1+(xm/x0-1)*exp(-r*(t-1997)))','t','xm','r','x0');
scatter(t,x,'k');
hold on;
plot(t,f(t,xm,r,x0),'r-');
xlabel('年份');
ylabel('人口数(万） ');
title('1997-2016 年实际人口与拟合值比较');
grid on;
x2017=f(2017,xm,r,x0),x2018=f(2018,xm,r,x0),x2023=f(2023,xm,r,x0)
x2028=f(2028,xm,r,x0),x2033=f(2033,xm,r,x0),x2038=f(2038,xm,r,x0)
x2043=f(2043,xm,r,x0),x2048=f(2048,xm,r,x0),x2053=f(2053,xm,r,x0)
x2058=f(2058,xm,r,x0),x2063=f(2063,xm,r,x0),x2068=f(2068,xm,r,x0)
z=2018:5:2068;y=[x2018,x2023,x2028,x2033,x2038,x2043,x2048,x2053,x2058,x206
3,x2068];
hold on;
plot(z,y,'--r');xlabel('年份');ylabel('人口数(万） ');title('曲线拟合以及人口
预测曲线')
grid on;

clc,clear
num=xlsread('C:\Users\\Desktop\Book1.xlsx','sheet1','B2:B21');
x1=num;
for i=1:18
m1(i+2)=(x1(i)+x1(i+1)+x1(i+2))/3;
end
for i=3:18
m2(i+2)=(m1(i)+m1(i+1)+m1(i+2))/3;
end
m1=m1';
m2=m2';
a=2*m1-m2;
b=m1-m2;
for i=1:52
y(:,i)=a(20,1)+b(20,1)*i;
end
y
figure;
x=1:1:52;
plot(x,y,'--r');
xlabel('年份');
ylabel('预测值');
legend('预测值');
title('2018-2068 年人口预测')

文章应用案例来自：http://t.csdn.cn/9cmBB