流形学习的观点是认为：我们所能观察到的数据实际上是由一个低维流形映射到高维空间上的。由于数据内部特征的限制，一些高维中的数据会产生维度上的冗余，实际上只需要比较低的维度就能唯一地表示。

举个例子，比如说我们在平面上有个圆，如何表示这个圆呢？如果我们把圆放在一个平面直角坐标系中，那一个圆实际上就是由一堆二维点构成的。

比如一个单位圆：（1,0）是一个在圆上的点，（0,1）也是一个在圆上的点，但（0,0）和（2,3）等等很多点是不在这个圆上的。显然如果用二维坐标来表示，我们没有办法让这个二维坐标系的所有点都是这个圆上的点。也就是说，用二维坐标来表示这个圆其实是有冗余的。

我们希望，如果能建立某一种描述方法，让这个描述方法所确定的所有点的集合都能在圆上，甚至能连续不间断地表示圆上的点，那就好了！有没有这种方法呢？对于圆来说，当然有！那就是用极坐标。在极坐标的表示方法下，圆心在原点的圆，只需要一个参数就能确定：半径。当你连续改变半径的大小，就能连续不断的产生“能被转换成二维坐标表示”的圆（产生很多圆）。所以说，实际上二维空间中的圆就是一个一维流形。

与之相似的，三维空间中一个球面，用x, y, z三个坐标轴确定时会产生冗余（很多在三维空间中的数据点并不在球面上）。但其实只需要用两个坐标就可以确定了，比如经度和维度。只要给定任何合法的经度和维度，我们就都能保证这个点肯定在球面上！

那么，流形学习有什么用呢？我现在能想到的主要有两个方面。

先说第一个方面。高维空间有冗余，低维空间没冗余。也就是说，流形可以作为一种数据降维的方式。传统很多算法都是用欧氏距离作为评价两个点之间的距离函数的。但是仔细想想这种欧氏距离直觉上并不靠谱。“我们只是看到了三维数据，就要用三维坐标系内的尺度去对事物进行评价？”总觉得有些怪怪的。

举个例子，从北京到上海有多远？你可以找一个地球仪，然后用一把能弯曲的软软的尺子，经过地球仪表面然后测量一下这两个点的距离。但是如果我用一根直线，将地球仪从北京到上海洞穿，测量出一个更短的距离，你一定会觉得我疯了。这说明，尽管你得到的北京和上海的坐标是三维空间坐标(x,y,z)，但使用欧氏距离对于“在高维空间展开的低维流型”进行距离的衡量是不正确的。

显然对于“从北京到上海的距离”这件事，我们关注的是把三维地球展开成二维平面，然后测量的地表上的距离，而不是三维空间中球面上两个点的欧氏距离。

既“流型空间上的可以用欧氏距离，不代表低维流型所展开的高维空间中也可以使用欧氏距离进行衡量”。只有在流型空间，用欧氏距离才有意义。

但实际上很多时候，尽管是高维空间，但出于简便，我们仍然近似使用欧氏距离。但通常来说效果都不会太好。不过我们通过一些变换，将原始的高维空间的数据映射但低维流型空间然后再用欧氏距离衡量。或者干脆用一种能够在高维空间更准确地度量距离的距离函数来替代欧氏距离。这样能取得更加合理的距离度量结果。

举个例子，假如说决策部门打算把一些离得比较近的城市聚成一堆，然后组建个大城市。这时候“远近”这个概念显然是指地表上的距离，因为说空间直线距离并没有什么意义。

而对于降维算法来说，如果使用传统的欧氏距离来作为距离尺度，显然会抛弃“数据的内部特征”。如果测量球面两点距离采用空间欧氏距离，那就会忽略掉“这是个球面”这个信息。

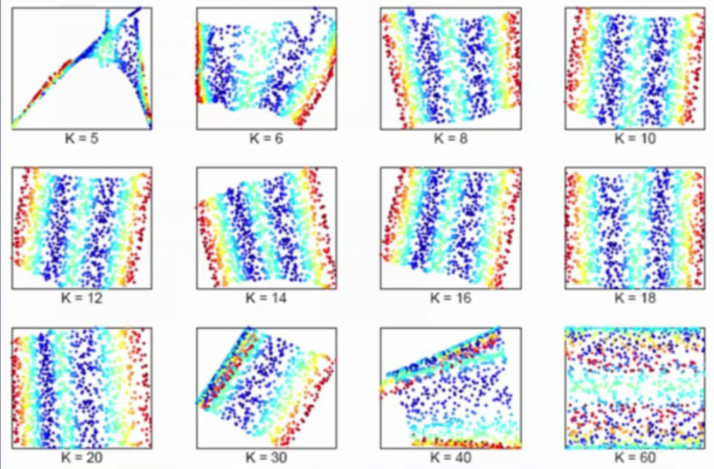
其实用一幅图就都明白了，那就是传说中的瑞士卷：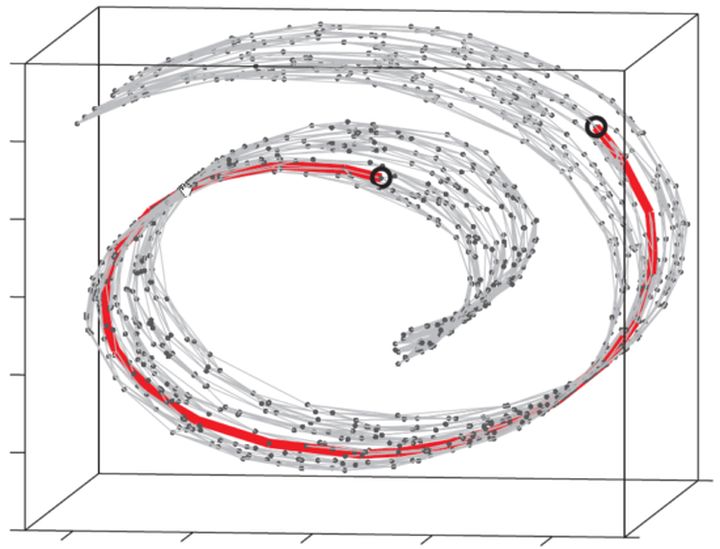

如果我们观察到的数据是三维的，但其本质是一个二维流形。图上所标注的两个圈圈，在流形（把卷展开）上本距离非常远，但是用三维空间的欧氏距离来计算则它们的距离要近得多。

所以说，流形学习的一个主要应用就是“非线性降维” 。而非线性降维因为考虑到了流形的问题，所以降维的过程中不但考虑到了距离，更考虑到了生成数据的拓扑结构。

第二个方面，流形能够刻画数据的本质。也就是说。既然学习到了“将数据从高维空间降维到低维空间，还能不损失信息”的映射，那这个映射能够输入原始数据，输出数据更本质的特征(就像压缩一样，用更少的数据能尽可能多地表示原始数据)。

深度学习主要的特点就是“特征学习”，所谓特征，就是能“表示事物本质的内容”，一般来说特征的维度应该小于数据本身。有一些实证证实，大脑处理数据其实是通过记忆、重现的方式。数据那么多，大脑怎么能一一记住？那就可以只记住“特征”！例如我们知道“人”都是两只眼睛一个鼻子一张嘴。而具体到每一个人则是再这个基本特征之上添加了一些其他的特异性的内容仅此而已。

深度学习一直以来就是在模仿大脑的结构，或者说在模仿大脑对数据的处理能力：从底层感受器输入原始数据，逐步求精得到特征。所谓的特征，在一定程度上就可以用流形的概念来解释。我们希望我们的模型能够学习到“数据在流型空间中的表示”。如果能做到这一点，则说明我们的模型离“模拟大脑”又前进了一步。

拓展一下，有一个有趣的事情：
我们如何来说明“模型学习到了流形”？前面提到了高维数据其实是由低维流形生成的。如果我们能模拟这个生成过程，再通过对低维流形的微调，应该能得到对应的“有意义且有道理”的高维数据。

下面是利用生成对抗网络（GAN）生成的人脸：

可以把生成过程看作：输入一个特征空间的低维编码，得到一个输出空间的高维图像。如何证明我们学习到的这个生成过程就是像人脑一样从低维流形映射到高维空间呢？还记得我们之前说过，流型空间一般应该是连续的，而映射到的高维空间的数据也应该在流形连续调整时变得连续且有意义。

再另一篇介绍了GAN的一个扩展的DCGAN的文章中，做了这样一件事：

寻找两个编码，这两个编码都能生成有意义的内容，将这两个编码插值得到好多编码。也就是说这些编码实际上描述了从编码A到编码B缓慢转变的过程。编码A是起点，编码B是目标，A和B之间的连续转变的编码则应该让生成的图像处于“从A向B”的过渡过程！事实如何呢？请看下图：

DCGAN这篇文章除了通过插值方法以外，还用了其他很多方法来验证编码空间是不是流型空间。我觉得这篇文章的贡献不只在于DCGAN这个模型，而在于后面很多实验的分析，毕竟是发在ICLR上的文章，搞的都是“特征工程”。其中的实验部分非常值得一看~

关于“冗余”，补充一下：

数据因为固有的特性，导致无法“填满”整个高维空间。例如如果数据只能出现在三维空间中的一个球面上。那这个球面以外的空间永远不会有数据点。而一个表面我们完全可以只用两个参数来表示(经度、维度)。所以这个球面是一个二维流型的三维展开。

在举个例子：身份证号。
我们的身份证号是18位的。但是身份证号有严格的格式：3位省3位市8位生日4位其他编码。这18位，最多能出现 10的18次方个不同的编码。但由于格式的限制，很多编码是不可能产生的。例如“999888777766554321”这就不可能出现。

但我们可以给每一个新出生的人一个连续的编码。只需要10位数字，就足够代表100亿人了。所以当我们有某种方法，能够找到一个从18维空间映射到10维空间的方法。那么这个10维空间就是数据“最本质”的特征了。

例如一张图片是256×256=65536维空间的。

如果我们能找到一个到2维空间的完美映射。就能得到“只需要用两个维度就能唯一地表示数据特征”的方法。例如两个维度可能是头转向的角度(上下、左右)。

那么只需要改变这个2维编码，再还原会65536维空间，再reshape成256×256的图片，就能得到同一张人脸连续地“转头”、“点头”的样子。

而流形学习就是在考虑：

1，如何找到这个从高维到低维的映射。

2，哪怕不能直接找到这个映射，那我们可以找到某种方法，在高维空间处理数据，等效于“将高维空间映射到低维空间、再处理数据、再映射回高维空间”的这种操作。

原文链接：https://www.zhihu.com/question/24015486/answer/194284643