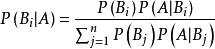贝叶斯处理多分类问题时,对于不同的数据特征要采用不同的贝叶斯变体。这里主要说下处理“连续型”变量的高斯贝叶斯分类和处理”离散型“变量的多项式贝叶斯分类。
回顾:贝叶斯公式

p(x):对于输入的每个x值是随机的,它们应该有相同的概率,所以P(x)不需要求解。
p(yk):表示先验知识,即 yk类别出现的频数/总样本数。
P(x|yk):对于贝叶斯的几种不同变体,主要是假设x在不同分布(高斯、伯努利、多项式分布…)下求P(x|yk)的概率值。
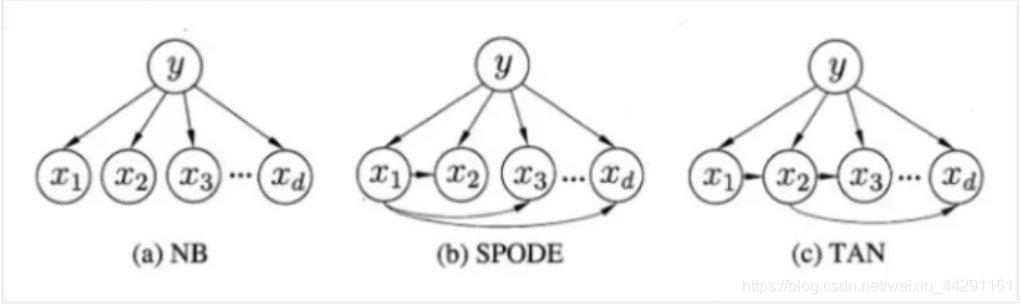
朴素贝叶斯:P(x|yk)在这里认为是相互独立,也就是说,xi,xj相互之间,则P(x|yk) = P(x1|yk)P(x2|yk)…P(xn|yk)。
贝叶斯的几种变体也就是P(x|yk)在不同分布下,求特征概率的方式不同而已。
1.高斯朴素贝叶斯
1.1 高斯概率分布
对于连续型特征,假设它们服从高斯分布,那么可以使用高斯贝叶斯。
高斯公式:

式中xi表示样本中的第i个特征,μ表示xi列的均值。σ表示xi列的方差。
通过高斯公式就可以得到每个特征出现的概率值。
计算在yk类条件下,特征xi的概率。然后将概率连乘求最大似然估计。
1.2 代码实现
class GaussianNB:def __init__(self):self.prior = Noneself.avgs = Noneself.vars = Noneself.n_class = None# 计算先验概率def _get_prior(self,label: array)->array:cnt = Counter(label)prior = np.array([cnt[i] / len(label) for i in range(len(cnt))])return prior# 计算训练集均值。每个label分别计算均值def _get_avgs(self, data: array, label: array)->array:return np.array([data[label == i].mean(axis=0) for i in range(self.n_class)])# 计算训练集方差。每一个特征的进行方差def _get_vars(self, data: array, label: array)->array:return np.array([data[label == i].var(axis=0) for i in range(self.n_class)])# 计算似然度,即公式-》P(x|yi)def _get_likelihood(self, row: array)->array:return (1 / sqrt(2 * pi * self.vars) * exp(-(row - self.avgs)**2 / (2 * self.vars))).prod(axis=1) # prod按行连乘# 训练模型def fit(self, data: array, label: array):self.prior = self._get_prior(label)self.n_class = len(self.prior)self.avgs = self._get_avgs(data, label)self.vars = self._get_vars(data, label)# 计算prob,先验概率乘以似然度再归一化得到每个label的prob def predict_prob(self, data: array)->array:likelihood = np.apply_along_axis(self._get_likelihood, axis=1, arr=data) # 基于data按行,调用_get_likehood函数probs = self.prior * likelihoodprobs_sum = probs.sum(axis=1)return probs / probs_sum[:, None]# 预测labeldef predict(self, data: array)->array:return self.predict_prob(data).argmax(axis=1)if __init__=="__main__":# 自己的数据和标签data,label = load(data)data_train, data_test, label_train, label_test = train_test_split(data, label, random_state=100)clf = GaussianNB()clf.fit(data_train, label_train)y_hat = clf.predict(data_test)
2.多项式朴素贝叶斯
2.1 多项式概率分布
对于文本分类任务,通过one-hot编码,将文本进行向量化。这种离散特征,就可以考虑基于多项式分布的贝叶斯。
其实就是基于极大似然估计的方法,把【词频/词频总数】 当做该词出现的概率再连乘。通俗的理解就是:这些词组合在一起,该文本是yk类的概率是多大。
多项式分布公式:

式中,yk表示在类别k条件下,xi表示样本的第i个词,样本的总长度是词袋的大小。N(yk,xi)表示在yk条件下xi这个次出现的频数,α是平滑因子,一般有α=1(拉普拉斯平滑)。N(yk)表示在条件yk下出现的总词数。
这里只需要将P(xi|yk),采用多项式分布计算在类yk条件下,特征xi的概率。然后将概率连乘求最大似然估计。
2.2 代码实现
#coding: utf-8
import numpy as np
import collectionsclass MultiNB:def __init__(self):self.prior = Noneself.word_freqs = Noneself.n_class = Nonedef _get_prior(self, label: np.array)-> np.array:cnt = collections.Counter(label)prior = np.array([cnt[i]/len(label) for i in range(len(cnt))])return priordef _get_word_freqs(self, data : np.array, label :np.array)-> np.array:word_freqs = []for i in range(self.n_class):num = data[label == i].sum(axis=0) + 1 # 分子加1 ,防止0,做平滑处理,1为拉普拉斯平滑denom = np.sum(data[label==i].sum(axis=0)) + 3 # 分母初始值,设为类别个数word_freqs.append(np.log(num/denom))return np.array(word_freqs)def _get_likelihood(self, row: np.array) -> np.array:return (row * self.word_freqs).sum(axis=1)def fit(self, data: np.array, label:np.array):self.prior = self._get_prior(label)self.n_class = len(self.prior)self.word_freqs = self._get_word_freqs(data, label)def predict_prob(self, data : np.array) -> np.array:likelihood = np.apply_along_axis(self._get_likelihood, axis=1, arr=data) # 这里求最大似然时,对多项式进行了取对数处理,否则相乘的话存在没有改单词的情况。probs = np.log(self.prior) + likelihoodprobs_sum = probs.sum(axis=1)return probs / probs_sum[:,None]def predict(self, data : np.array) -> np.array:return self.predict_prob(data).argmax(axis=1)def text_process(doclist, classlist):def createVocablist(doclist: list) -> list:"""返回所有文本中所有词的集合"""vocabSet = set([])for document in doclist:vocabSet = vocabSet | set(document)return list(vocabSet)def setOfWord2Vec(vocablist: list, inputSentence: list) -> list:"""生成词频矩阵"""returnVec = [0] * len(vocablist)for word in inputSentence:if word in vocablist:returnVec[vocablist.index(word)] = 1return returnVec# 构建词袋vocablist = createVocablist(doclist)# doc进行one-hot编码docMat = [setOfWord2Vec(vocablist,doc) for doc in doclist]return np.array(docMat),np.array(classlist)if __name__ == '__main__':doclist = [['2021', '年', '12', '月', '21', '日'],['云投', '集团', '与', '云南', '交投', '就', '本次'],['无偿', '划转', '事项', '签署', '了', ' '],['《', '国有', '股权', '无偿', '划转', '协议', '》', ',', ' ']]classlist = [0,1,2,1]x_train, y_train = text_process(doclist, classlist)clf = MultiNB()clf.fit(np.array(x_train),np.array(y_train))res = clf.predict(x_train)
注意:就像在代码里说的,这里是求log(P(yk|x)) = ∑log(P(x|yk))+log(P(yk)),因为在进行one-hot编码是,有些文本里面是不存在词袋里的词的,最大似然估计求∏,存在0的情况。所以做了取对数处理。
参考:
https://zhuanlan.zhihu.com/p/64498790
https://scikit-learn.org.cn/search/index?searchkey
贝叶斯应用举例——垃圾邮件