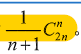朴素贝叶斯分类的概念(一)

朴素贝叶斯模型是一组非常简单快速的分类算法,通常适用于维度非常高的数据集.速度快,可调参数少.非常适合为分类问题提供快速粗糙的基本方案.

作为一个数学小白,乍一听到朴素贝叶斯这个名词时一般都是晕的,根据多年的初等数学学习经验,贝叶斯应该是一个人,但是"朴素"是什么鬼?是不是还有不朴素的贝叶斯?其实我看这个模型已经好多次了.每一次看到那堆数学公式的时候我都是直接跳过看结论的.不过现在想想学习这件事情不能这么马虎,这么基础的一个概念,放在茫茫大算法中算是小儿科的存在,如果连这个都没搞懂那以后的机器学习算法还怎么看,以后论文还怎么看?于是我开始对贝叶斯定理做了一个较为完整的学习.也和大家一起分享一下

首先要说一下贝叶斯定理

在说贝叶斯定理前先说几个专有名词

条件概率,条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为：P(A|B)，读作“在B条件下A的概率”。举个例子,事件A是这个人是女生,事件B是这个人扎小辫子.那么P(A|B)就是在这个人扎小辫子的情况下,这个人是女生的概率
先验概率,先验概率是指根据以往经验和分析得到的概率,如全概率公式,它往往作为"由因求果"问题中的"因"出现的概率。
全概率公式:全概率公式为概率论中的重要公式，它将对一复杂事件A的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题。内容：如果事件B1、B2、B3…Bn 构成一个完备事件组,即它们两两互不相容,其和为全集;并且P(Bi)大于0,则对任一事件A有P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|Bn)P(Bn)或p(A)=P(AB1)+P(AB2)+...+P(ABn))，其中A与Bn的关系为交)
条件独立:如果P(X,Y|Z)=P(X|Z)P(Y|Z),或等价地P(X|Y,Z)=P(X|Z)则称事件X,Y对于给定事件Z是条件独立的,也就是说,当Z发生时,X发生与否与Y发生与否是无关的.

贝叶斯定理也可以简单的表示为

P(A|B)=P(A)P(B|A)/P(B)

或者它的复杂版本

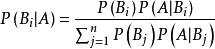
这个公式有啥实际应用价值呢?听着貌似有点绕但好像并没有什么鸟用啊.

我引用百度百科的一个例子来说明

贝叶斯定理在检测吸毒者时很有用。假设一个常规的检测结果的敏感度与可靠度均为99%，也就是说，当被检者吸毒时，每次检测呈阳性（+）的概率为99%。而被检者不吸毒时，每次检测呈阴性（-）的概率为99%。从检测结果的概率来看，检测结果是比较准确的，但是贝叶斯定理却可以揭示一个潜在的问题。假设某公司将对其全体雇员进行一次鸦片吸食情况的检测，已知0.5%的雇员吸毒。我们想知道，每位医学检测呈阳性的雇员吸毒的概率有多高？令“D”为雇员吸毒事件，“N”为雇员不吸毒事件，“+”为检测呈阳性事件。可得

P(D)代表雇员吸毒的概率，不考虑其他情况，该值为0.005。因为公司的预先统计表明该公司的雇员中有0.5%的人吸食毒品，所以这个值就是D的先验概率。
P(N)代表雇员不吸毒的概率，显然，该值为0.995，也就是1-P(D)。
P(+|D)代表吸毒者阳性检出率，这是一个条件概率，由于阳性检测准确性是99%，因此该值为0.99。
P(+|N)代表不吸毒者阳性检出率，也就是出错检测的概率，该值为0.01，因为对于不吸毒者，其检测为阴性的概率为99%，因此，其被误检测成阳性的概率为1-99%。
P(+)代表不考虑其他因素的影响的阳性检出率。该值为0.0149或者1.49%。我们可以通过全概率公式计算得到：此概率 = 吸毒者阳性检出率（0.5% x 99% = 0.00495)+ 不吸毒者阳性检出率（99.5% x 1% = 0.00995)。P(+）=0.0149是检测呈阳性的先验概率。用数学公式描述为：
根据上述描述，我们可以计算某人检测呈阳性时确实吸毒的条件概率P(D|+)：

P(D|+) = P(+|D)P(D)/(P(+|D)P(D)+P(+|N)P(N))=0.99 *0.005/0.0149=0.332215

尽管我们的检测结果可靠性很高，但是只能得出如下结论：如果某人检测呈阳性，那么此人是吸毒的概率只有大约33%，也就是说此人不吸毒的可能性比较大。我们测试的条件（本例中指D，雇员吸毒）越难发生，发生误判的可能性越大。

但如果让此人再次复检（相当于P(D)=33.2215%，为吸毒者概率，替换了原先的0.5%），再使用贝叶斯定理计算，将会得到此人吸毒的概率为98.01%。但这还不是贝叶斯定理最强的地方，如果让此人再次复检，再重复使用贝叶斯定理计算，会得到此人吸毒的概率为99.8%（99.9794951%）已经超过了检测的可靠度。

所以大家可以看到在检测学上,先验条件很重要,很多人都会潜意识的认为P(A|B)约等于P(B|A),实际上这两个关系差别有可能会非常大.吸毒的人检测到的敏感度是阳性的概率是99%,那么大家潜意识里面就会认为敏感度检测到阳性99%就是吸毒的了.实际上这个是有问题的.拿我一开始举的例子来说,穿裙子的人是女生的概率为99%,但是女生一定会穿裙子吗?这得看今天一共有多少人穿裙子来了.

写到这里要补充一段了,我把以上的文字给了一位不懂贝叶斯的人看了一遍,她提了两个问题:

在百度百科关于吸毒者的这个例子里面有这么一段

我们测试的条件（本例中指D，雇员吸毒）越难发生，发生误判的可能性越大。但如果让此人再次复检（相当于P(D)=33.2215%，为吸毒者概率，替换了原先的0.5%），再使用贝叶斯定理计算，将会得到此人吸毒的概率为98.01%。但这还不是贝叶斯定理最强的地方，如果让此人再次复检，再重复使用贝叶斯定理计算，会得到此人吸毒的概率为99.8%（99.9794951%）已经超过了检测的可靠度。

她的问题是:为什么这个人再一次复检的时候吸毒概率是98%了?如果换到我另外一个例子里面的话,第一次检测到一个人是女孩子如果她穿裙子的概率是33%,那么第二次再检查一下这个女孩子她穿裙子的概率就是98%了吗?完全不符合逻辑啊

当时我被她这个举例一把问懵了.好像很有道理的样子.但是实际上是举例子的问题,在吸毒者的那个例子里面,吸毒者第一次检测是阳性,但是这个结果可能是环境误差导致的,下一次检测的时候是否是阳性是概率性问题.但是一个人检测到是女孩子,那么下一次她再检测不是女孩子的概率我只能说很低,除非她这个过程抽空去做了一个变性手术.这里面的最大问题是事件"这个人是个女孩子"和"检测"这个动作的关系,检测这个动作往往都带有时间和空间属性,在吸毒者的事件里面,我们把这个事件表述的详细一些,假设我们的检测时间间隔半天,并且使用A仪器进行检测.那么"雇员在上午使用A仪器检测到是阳性"这个事件就里面的时间和地点就会影响到事件的最终结果,因此是一个相对随机的事件.但是换到"这个人上午在操场上检测到是女孩子"这个事件,我不认为这个人下午去教室里面就会检测到是男孩子.所以在时间空间上并没有影响.所以百度的这个例子是有一定的实际运用场景下给出的.需要具体问题具体分析.

说完了贝叶斯定理,下面来说一说朴素贝叶斯定理是什么玩意儿

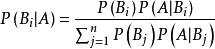
朴素贝叶斯定理的朴素,是指给定目标下,贝叶斯定理中的各个条件互相独立,即公式中的B1,B2,.....Bn互相独立

再回忆一下刚才我们写到的什么是条件独立,条件独立的公式:P(X,Y|Z)=P(X|Z)P(Y|Z)

好了,又到了举例子的时间了.我们举例恒大今天对战权健的比赛

根据贝叶斯定理

P(恒大赢球|上郜林,上金英权,上曾诚,上高拉特) = P(恒大赢球)*P(上郜林,上金英权,上曾诚,上高拉特|恒大赢球)/P(上郜林,上金英权,上曾诚,上高拉特)

再根据朴素贝叶斯的规则:所有的条件都是独立的.也就是说

P(上郜林,上金英权,上曾诚,上高拉特) = P(上郜林)*P(上金英权)*P(上曾诚)*P(上高拉特)

将这个代入原式中,可以得到

根据样本数据,我们可以很轻易的统计到等式右边的几个概率.

这里就会有同学问了:"等等等等,为啥要假设条件之间是相互独立的呢?"

因为实际的统计中,条件远远不止这么几个,如果有几十个条件的话,想要求出类似于P(上郜林,上金英权,上曾诚,上高拉特|恒大赢球)的概率就会发现由于数据的稀疏性,统计出来的结果往往很有可能是0.这样的统计结果是不合适也是没有意义的.