贝叶斯定理

贝叶斯定理是由已知事件概率和条件概率计算未知条件概率的概率推理算法，其公式如下：
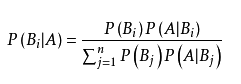
贝叶斯公式
其中，P(Bi|A)是要计算的目标条件概率，表示事件 A 发生的条件下，事件 Bi 发生的概率。Bi 为互斥且完整的事件 B1，B2，……，Bn 中的一项
P(Bi)P(A|Bi)是联合概率P(A Bi)，表示事件 A 和事件 Bi 同时发生的概率
∑ⁿ_j=1P(Bj)P(A|Bj)的结果为随机事件 A 发生的概率

贝叶斯分类算法是贝叶斯定理在统计学中的一项应用，基于贝叶斯分类算法实现的贝叶斯分类器是可以媲美决策树和人工神经网络分类的强大分类器，具有方法简单、准确率高、速度快的特点

朴素贝叶斯

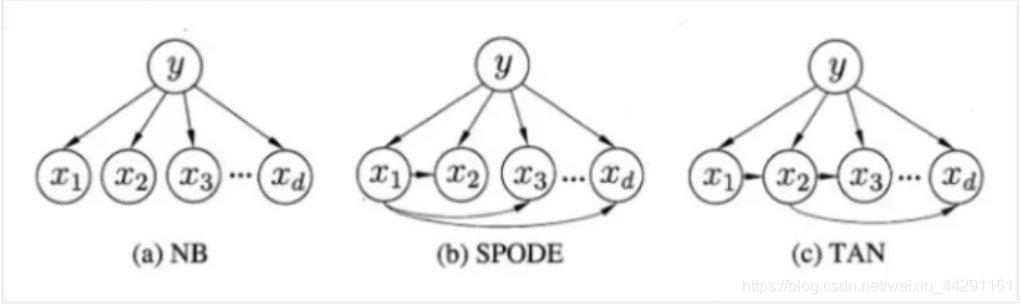
朴素贝叶斯分类是基于特征条件独立假设下的贝叶斯分类算法，它和决策树分类是目前应用最为广泛的两个分类模型
特征条件独立假设，即假定实例的各个属性互相独立，互不影响

假设有 n 个类别 C1，C2，……，Cn，给定一个实例的特征向量 w，则此实例属于类 Ci 的概率为
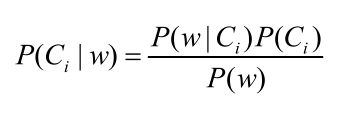
朴素贝叶斯分类公式
P(w|Ci)的计算：
w 是特征向量，若将其展开，则可将P(w|Ci)写作P(w0,w1,w2,…,wn|Ci)，由特征条件独立的假设，即有如下运算

P(w|Ci) = P(w0|Ci)P(w1|Ci)P(w2|Ci)…P(wn|Ci)

朴素贝叶斯分类基于特征独立假设的条件，但现实世界中各属性之间往往不是互相独立的，或多或少都存在互相依赖的关系。但即使是在这样的条件下，朴素贝叶斯分类仍然可以得到较为接近真实情况的分类结果

源代码

下面是我用 Python3.7 写的一个朴素贝叶斯的分类器

# naive_bayes.py  -- 朴素贝叶斯import mathclass NB():def __init__(self):self.cla_all_num = 0self.cla_num = {}self.cla_tag_num = {}self.landa = 1  # 拉普拉斯修正值def train(self, taglist, cla):  # 训练，每次插入一条数据# 插入分类self.cla_all_num += 1if cla in self.cla_num:  # 是否已存在该分类self.cla_num[cla] += 1else:self.cla_num[cla] = 1if cla not in self.cla_tag_num:self.cla_tag_num[cla] = {}  # 创建每个分类的标签字典# 插入标签tmp_tags = self.cla_tag_num[cla]  # 浅拷贝，用作别名for tag in taglist:if tag in tmp_tags:tmp_tags[tag] += 1else:tmp_tags[tag] = 1def P_C(self, cla):  # 计算分类 cla 的先验概率return self.cla_num[cla] / self.cla_all_numdef P_all_C(self):  # 计算所有分类的先验概率tmpdict = {}for key in self.cla_num.keys():tmpdict[key] = self.cla_num[key] / self.cla_all_numreturn tmpdictdef P_W_C(self, tag, cla):  # 计算分类 cla 中标签 tag 的后验概率tmp_tags = self.cla_tag_num[cla]  # 浅拷贝，用作别名if tag not in self.cla_tag_num[cla]:return self.landa / (self.cla_num[cla] + len(tmp_tags) * self.landa)  # 拉普拉斯修正return (tmp_tags[tag] + self.landa) / (self.cla_num[cla] + len(tmp_tags) * self.landa)def test(self, test_tags):  # 测试res = ''res_P = Nonefor cla in self.cla_num.keys():log_P_W_C = 0for tag in test_tags:log_P_W_C += math.log(self.P_W_C(tag, cla))tmp_P = log_P_W_C + math.log(self.P_C(cla))  # P(w|Ci) * P(Ci)if res_P is None:res = clares_P = tmp_Pif tmp_P > res_P:res = clares_P = tmp_Preturn resdef set_landa(self, landa):self.landa = landadef clear(self):  # 重置模型self.cla_all_num = 0self.cla_num.clear()self.cla_tag_num.clear()

这里有几个需要注意的点：

零概率问题：
零概率问题，即测试样例的标签属性中，出现了模型训练过程中没有记录的值，或者某个分类没有记录的值，从而出现该标签属性值的出现概率 P(wi|Ci) = 0 的现象。因为 P(w|Ci) 等于各标签属性值 P(wi|Ci) 的乘积，当分类 Ci 中某一个标签属性值的概率为 0，最后的 P(w|Ci) 结果也为 0。很显然，这不能真实地代表该分类出现的概率

解决方法：
拉普拉斯修正，又叫拉普拉斯平滑，这是为了解决零概率问题而引入的处理方法。其修正过程：

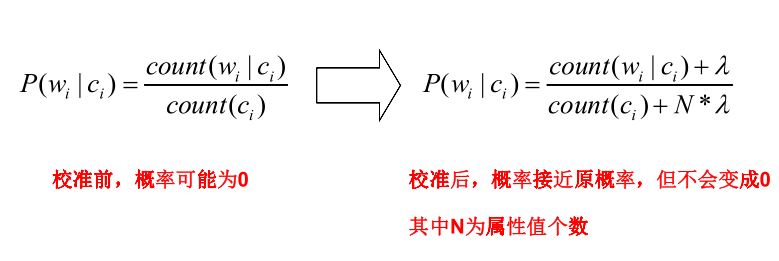
在源码中的体现：

def P_W_C(self, tag, cla):  # 计算分类 cla 中标签 tag 的后验概率tmp_tags = self.cla_tag_num[cla]  # 浅拷贝，用作别名if tag not in self.cla_tag_num[cla]:return self.landa / (self.cla_num[cla] + len(tmp_tags) * self.landa)  # 拉普拉斯修正return (tmp_tags[tag] + self.landa) / (self.cla_num[cla] + len(tmp_tags) * self.landa)

浮点数溢出问题：
在计算 P(w|Ci) 时，各标签属性概率的值可能很小，而很小的数再相乘，可能会导致浮点数溢出

解决方法：
对 P(w|Ci) 取对数，把概率相乘转换为相加
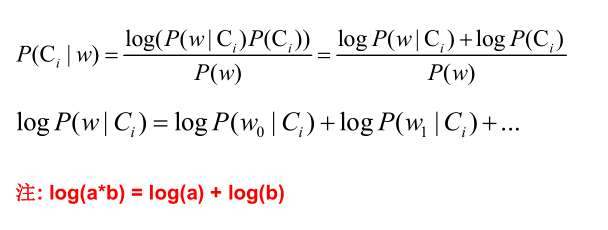
概率取对数
在源码中的体现：

for cla in self.cla_num.keys():log_P_W_C = 0for tag in test_tags:log_P_W_C += math.log(self.P_W_C(tag, cla))tmp_P = log_P_W_C + math.log(self.P_C(cla))  # P(w|Ci) * P(Ci)

在这里，因为概率 P(w|Ci) 的值为小于 1 的小数，取对数后的结果 log_P_W_C 为负值，不能直接与 P(Ci) 相乘。否则，可能出现相反的结果
不妨把 P(Ci) 的值也取对数，结果相加。因为对数是单调曲线，这并不影响最后的决策结果

样例测试

有如下样例，
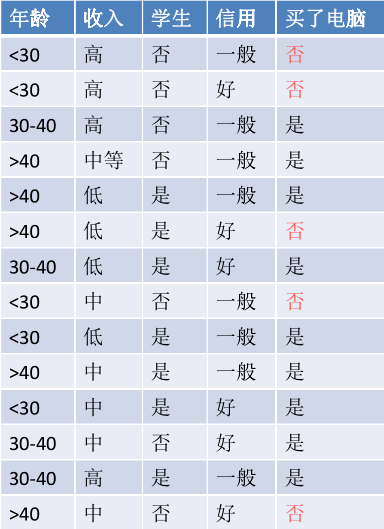
测试数据集
这里共有两个分类： “买了电脑” 和 “未买电脑”
每个训练实例有 4 个属性： “年龄”，“收入”，“是否学生”，“信用等级”

训练模型的代码如下：


if __name__ == '__main__':nb = NB()  # 生成模型# 训练模型# 年龄，收入，是否学生，信用等级  --->  是否买了电脑nb.train(['<30', '高', '否', '一般'], '否')nb.train(['<30', '高', '否', '好'], '否')nb.train(['30-40', '高', '否', '一般'], '是')nb.train(['>40', '中', '否', '一般'], '是')nb.train(['>40', '低', '是', '一般'], '是')nb.train(['>40', '低', '是', '好'], '否')nb.train(['30-40', '低', '是', '好'], '是')nb.train(['<30', '中', '否', '一般'], '否')nb.train(['<30', '低', '是', '一般'], '是')nb.train(['>40', '中', '是', '一般'], '是')nb.train(['<30', '中', '是', '好'], '是')nb.train(['30-40', '中', '否', '好'], '是')nb.train(['30-40', '高', '是', '一般'], '是')nb.train(['>40', '中', '否', '好'], '否')

模型训练好了

我们再给出一个测试实例：(年龄<30，收入中等，是学生，信用一般)

测试模型的代码如下：

	# 测试模型testdata = ['<30', '中', '是', '一般']print('测试结果：', nb.test(testdata))

运行结果：

结果显示，Ta 买了电脑

再计算验证一下

w = ( 年龄 <30，收入中等，是学生，信用一般 )
P(w|Ci) = P(w0|Ci) ) * P(w1|Ci) * P(w2|Ci) * P(w3|Ci)

计算 P(w|买了电脑) ：

P( 买了电脑 ) = 9/14 = 0.643
P( 年龄<30 | 买了电脑 ) = 2/9 = 0.222
P( 收入中等 | 买了电脑 ) = 4/9 = 0.444
P( 是学生 | 买了电脑 ) = 6/9 = 0.667
P( 信用一般 | 买了电脑 ) = 6/9 = 0.667
P( w | 买了电脑 ) = 0.222 * 0.444 * 0.667 * 0.667 = 0.044
P( w | 买了电脑 ) * P( 买了电脑 ) = 0.044 * 0.643 = 0.028

计算 P(w| 未买电脑 ) ：

P( 未买电脑 ) = 5/14 = 0.357
P( 年龄<30 | 未买电脑 ) = 3/5 = 0.600
P( 收入中等 | 未买电脑 ) = 2/5 = 0.400
P( 是学生 | 未买电脑 ) = 1/5 = 0.200
P( 信用一般 | 未买电脑 ) = 2/5 = 0.400
P( w | 未买电脑 ) = 0.6 * 0.4 * 0.2 * 0.4 = 0.019
P( w | 未买电脑 ) * P( 未买电脑 ) = 0.019 * 0.357 = 0.007

则有，
P( 买了电脑 | w ) = P( w | 买了电脑 ) * P( 买了电脑 ) / P(w) = 0.028 / P(w)
P( 未买电脑 | w ) = P( w | 未买电脑 ) * P( 未买电脑 ) / P(w) = 0.007 / P(w)

很显然 P( 买了电脑 | w ) > P( 未买电脑 | w ) ，结果是买了电脑