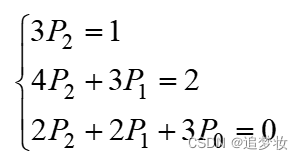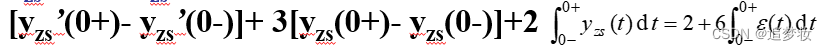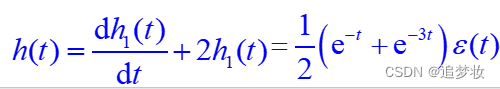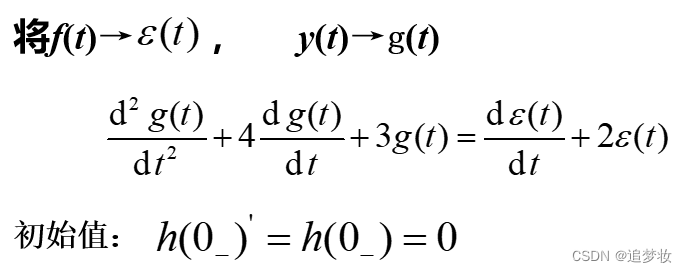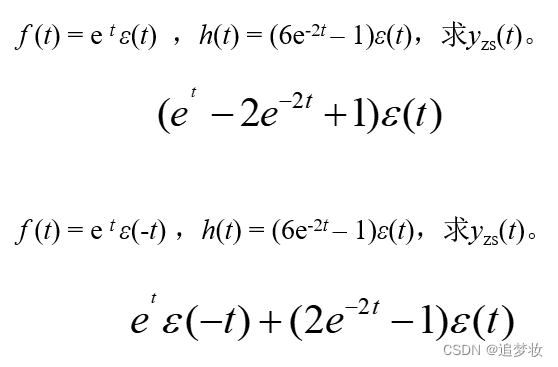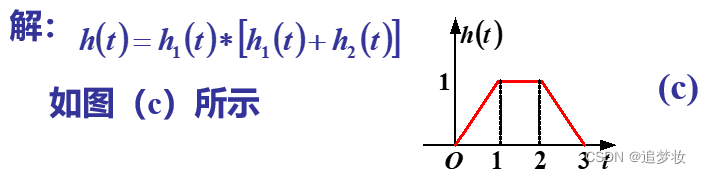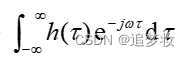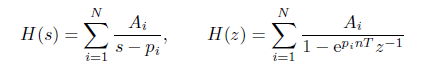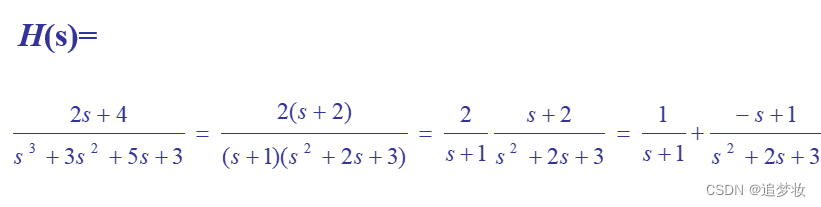2.1 LTI连续系统的响应
前言
LTI连续系统的时域分析,归结为:建立并求解线性微分方程。
由于在其分析过程涉及的函数变量均为时间t,故称为时域分析法。这种方法比较直观,物理概念清楚,是学习各种变换域分析法的基础。
一、微分方程的经典解
微分方程的经典解:完全解 = 齐次解 + 特解。
1. 齐次解
由特征方程→求出特征根→写出齐次解形式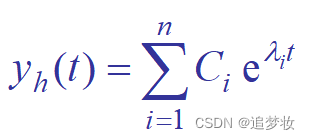
注意重根情况处理方法
齐次解举例
例
解 系统的特征方程为
特征根
对应的齐次解为

2. 特解
根据微分方程右端函数式形式,设含待定系数的特解函数式→代入原方程,比较系数定出特解。
特解
特解举例
例 给定微分方程式如果已知:
,分别求两种情况下此方程的特解。
解 (1)由于f(t)=t^2,故特解函数式为

这里,P2, P1, P0,将此式代入方程得到
等式两端各对应幂次的系数应相等,于是有
联解得到
所以,特解为
(2)当f(t)= e^t 时,特解为yp(t)=P e^t ,这里,P是待定系数。
代入方程后有:,
3. 全解
由初始值定出齐次解中的待定常数Ci。
全解举例
例 描述某系统的微分方程为 y”(t) + 5y’(t) + 6y(t) = f(t)
求(1)当f(t) = 2e^(-t),t≥0;y(0)=2,y’(0)= -1时的全解;
(2)当f(t) = e^(-2t),t≥0;y(0)= 1,y’(0)=0时的全解。
解(1) 特征方程为λ^2 + 5λ+ 6 = 0 其特征根λ1= – 2,λ2= – 3。齐次解为 yh(t) = C1e^( – 2t) + C2e^ (– 3t)
当f(t) = 2e^ (– t)时,其特解可设为 yp(t) = Pe^ (– t)
将其代入微分方程得
Pe^ (– t) + 5(– Pe^ (– t)) + 6Pe^ (– t) = 2e^ (– t) 解得 P=1
于是特解为 yp(t) = e^ (– t)
全解为: y(t) = yh(t) + yp(t) = C1e^ (–2t)+ C2e ^ (–3t) + e^ (– t)其中 待定常数C1,C2由初始条件确定。
y(0) = C1+C2+ 1 = 2,y’(0) = – 2C1 – 3C2 – 1= – 1
解得 C1 = 3 ,C2 = – 2
最后得全解 y(t) = 3e^ (– 2t)– 2e^ (–3t) + e ^ (– t) , t≥0(2)齐次解同上。当激励f(t)=e–2t时,其指数与特征根之一相重。故其特解为
yp(t) = (P1t + P0)e ^ (–2t)
代入微分方程可得 P1e ^ (–2t) = e ^ (–2t)
所以 P1= 1 但P0不能求得。特解为
yp(t) = (t + P0)e ^ (–2t)
全解为
y(t)= C1e–2t + C2e ^ (–3t)+ te ^ (–2t)+ P0e ^ (–2t)
= (C1+P0)e ^ (–2t)+C2e ^ (–3)+ te ^ (–2t)
将初始条件代入,得
y(0) = (C1+P0) + C2=1 ,y’(0)= –2(C1+P0) –3C2+1=0
解得 C1 + P0 = 2 ,C2= –1 最后得微分方程的全解为
y(t) = 2e ^ (–2t) – e ^ (–3t) + te ^ (–2t) , t≥0
上式第一项的系数C1+P0= 2,不能区分C1和P0,因而也不能区分自由响应和强迫响应。
其他
齐次解的函数形式仅与系统本身的特性有关,而与激励f(t)的函数形式无关,称为系统的固有响应或自由响应;
特解的函数形式由激励确定,称为强迫响应。
二、关于0-和0+初始值
介绍
若输入f(t)是在t=0时接入系统,则确定待定系数Ci时用t = 0+时刻的初始值,即y(j)(0+) (j=0,1,2…,n-1)。
而y(j)(0+)包含了输入信号的作用,不便于描述系统的历史信息。
在t=0-时,激励尚未接入,该时刻的值y(j)(0-)反映了系统的历史情况而与激励无关。称这些值为初始状态或起始值。
通常,需要从已知的初始状态y(j)(0-)设法求得y(j)(0+)。
当微分方程右端含有冲激函数时,响应y(t)及其各阶导数中,有些在t=0处将发生跃变。否则不会跃变。
0-和0+初始值举例1
例 描述某系统的微分方程为 y”(t) + 3y’(t) + 2y(t) = 2f’(t) + 6f(t)
已知y(0-)=2,y’(0-)= 0,f(t)=ε(t),求y(0+)和y’(0+)。
解 将输入f(t)=ε(t)代入上述微分方程得 y”(t) + 3y’(t) + 2y(t) = 2δ(t) + 6ε(t) (1)
利用系数匹配法分析:上式对于t=0-也成立,在0-<t<0+区间等号两端δ(t)项的系数应相等。
由于等号右端为2δ(t),故y”(t)应包含冲激函数,从而y’(t)在t= 0处将发生跃变,即y’(0+)≠y’(0-)。
但y’(t)不含冲激函数,否则y”(t)将含有δ’(t)项。由于y’(t)中不含δ(t),故y(t)在t=0处是连续的。故 y(0+) = y(0-) = 2
对式(1)两端积分有由于积分在无穷小区间[0-,0+]进行的,且y(t)在t=0连续,故
于是由上式得 [y’(0+) – y’(0-)] + 3[y(0+) – y(0-)]=2
考虑 y(0+) = y(0-)=2 ,所以 y’(0+) – y’(0-) = 2 , y’(0+) = y’(0-) + 2 =2
0-和0+初始值举例2
例 描述某系统的微分方程为 y”(t) + 3y’(t) + 2y(t) = 2f’(t) + f(t)
已知y(0-)=2,y’(0-)= 0,f(t)=δ’(t),求y(0+)和y’(0+)。
解 将输入f(t)=δ’(t)代入上述微分方程得 y”(t) + 3y’(t) + 2y(t) = 2δ” (t) + δ’(t) (1)
利用系数匹配法分析:
令y”(t)=aδ” (t)+bδ’(t)+Cδ(t)+r1(t), r1(t)中不含冲激
y’(t)= aδ’(t)+bδ(t)+ r2(t), r2(t)=Cε(t)+ r1(-1)(t)
y(t)= aδ(t)+ r3(t), r3(t)=bε(t)+ r2(-1)(t)
将上述关系代入式(1),并整理得aδ” (t)+ bδ’(t)+ Cδ(t) + r1(t)
+3aδ’(t)+ 3bδ(t)+ 3r2(t)
+ 2aδ(t)+ 2r3(t) = 2δ” (t) + δ’(t)
比较等式两边冲激项系数,有
a=2
b+3a=1
c+3b+2a=0解得:a=2,b=-5,c=11,故
y”(t)=2δ” (t)- 5δ’(t) + 11δ(t) + r1(t),
y’(t)= 2δ’(t) - 5δ(t) + r2(t),
y(t)= 2δ(t) + r3(t)。对y”(t)从0-到0+积分得 y’(0+)-y’(0-) =11, y’(0+)=y’(0-) +11= 11
对y’(t)从0-到0+积分得 y(0+)-y(0-) =-5, y(0+)=y(0-)-5 = 2-5=-3
三、零输入响应
定义:零输入响应是激励为零时仅由系统的初始状态{x(0)}所引起的相应,用y zi (t)表示
四、零状态响应
定义:零状态响应是系统的初始状态为零时,仅由输入状态f(t)引起的响应,用y zs (t)表示
五、全响应
y(t) = yzi(t) + yzs(t) ,也可以分别用经典法求解。
注意:对t=0时接入激励f(t)的系统,初始值 yzi(j)(0+), yzs(j)(0+) (j = 0,1,2,…,n-1)的计算。
y(j)(0-)= yzi(j)(0-)+ yzs(j)(0-)
y(j)(0+)= yzi(j)(0+)+ yzs(j)(0+)
对于零输入响应,由于激励为零,故有 yzi(j)(0+)= yzi(j)(0-) = y (j)(0-)
对于零状态响应,在t=0-时刻激励尚未接入,故应有 yzs(j)(0-)=0
yzs(j)(0+)的求法下面举例说明。
零输入响应和零状态响应举例
例 描述某系统的微分方程为 y”(t) + 3y’(t) + 2y(t) = 2f’(t) + 6f(t)
已知y(0-)=2,y’(0-)=0,f(t)=ε(t)。求该系统的零输入响应和零状态响应。
解(1)零输入响应yzi(t) 激励为0 ,故yzi(t)满足
yzi”(t) + 3yzi’(t) + 2yzi(t) = 0
yzi(0+)= yzi(0-)= y(0-)=2
yzi’(0+)= yzi’(0-)= y’(0-)=0
该齐次方程的特征根为–1, – 2,故
yzi(t) = Czi1e^ (–t) + Czi2e^ (–2t)
代入初始值并解得系数为Czi1=4 ,Czi2= – 2 ,代入得
yzi(t) = 4e^ (–t) – 2e^ (–2t) ,t > 0(2)零状态响应yzs(t) 满足
yzs”(t) + 3yzs’(t) + 2yzs(t) = 2δ(t) + 6ε(t) 并有 yzs(0-) = yzs’(0-) = 0
由于上式等号右端含有δ(t),故yzs”(t)含有δ(t),从而yzs’(t)跃变,即yzs’(0+)≠yzs’(0-),而yzs(t)在t = 0连续,即yzs(0+) = yzs(0-) = 0,积分得因此,yzs’(0+)= 2 + yzs’(0-)=2
对t>0时,有 yzs”(t) + 3yzs’(t) + 2yzs(t) = 6
不难求得其齐次解为Czs1e^ (–t)+ Czs2e^ (–2t),其特解为常数3,
于是有 yzs(t)=Czs1e^ (–t) + Czs2e^ (–2t)+ 3
代入初始值求得 yzs(t)= – 4e^ (–t) + e^ (–2t)+ 3 ,t≥0
2.2 冲激响应和阶跃响应
一、冲激响应
定义:
由单位冲激函数δ(t)所引起的零状态响应称为单位冲激响应,简称冲激响应,记为h(t)。
h(t)=T[{0},δ(t)]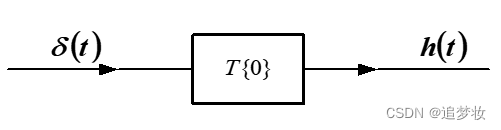
系统冲激响应的求解
冲激响应的数学模型
对于LTI系统,可以用一n阶微分方程表示 
h(t)解答的形式
由于δ(t)及其导数在 t≥0+ 时都为零,因而方程式右端的自由项恒等于零,这样原系统的冲激响应形式与齐次解的形式相同。
①与特征根有关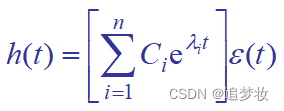
②与n, m相对大小有关 
冲激响应求解举例
例 求系统的冲激响应。
解 将f(t)→δ(t), y(t)→h(t)
解法一:线性时不变性质法
设h1(t)满足简单方程
将边界条件代入h1(t)式,解得 C1=1/2, C2=-1/2,
则由系统的线性时不变特性
解法二:求特征根
,h(t)中不包含冲激项
冲激响应
,记得需要带ε(t)
两种求待定系数方法:求0+法,奇异函数项相平衡法
求0+法
奇异函数项相平衡法
基本单元的冲激响应(数乘器、延时器、微分器、积分器)
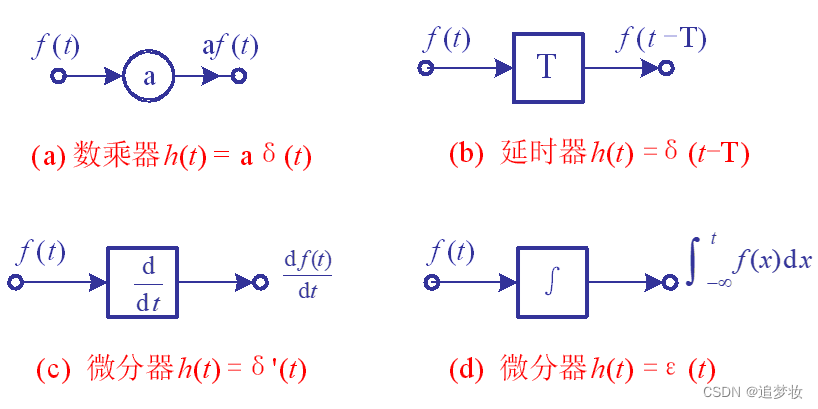
二、阶跃响应
定义
一个LTI系统,当其初始状态为零时,输入为单位阶跃函数所引起的响应称为单位阶跃响应,简称阶跃响应,用g(t)表示。
说明
冲激响应求解举例
例 系统的阶跃激响应。
解
2.3 零状态响应与卷积积分
一、任意激励下的零状态响应

二、卷积积分
定义

用定义计算卷积举例
例 f(t) = e^ t ,(-∞<t<∞),h(t) = (6e^(-2t) – 1)ε(t),求yzs(t)。
解其他思考题
卷积的图解法

卷积过程可分解为五步:
(1)换元: t换为τ→得 f1(τ), f2(τ)
(2)反转:由f2(τ)反转→ f2(–τ)
(3)平移:由 f2(–τ)右移t → f2(t-τ)
(4)乘积: f1(τ) f2(t-τ)
(5)积分: τ从 –∞到∞对乘积项积分。
注意:t为参变量。
求某一时刻卷积值
例 f1(t)、 f2(t)如图所示,已知f(t) = f2(t)* f1(t),求f(2) =?
解
(1)换元
(2) f1(τ)得f1(–τ)
(3) f1(–τ)右移2得f1(2–τ)
(4) f1(2–τ)乘f2(τ)
(5)积分,得f(2) = 0(面积为0)
图解法计算卷积举例
例 f (t) ,h(t) 如图所示
,求yzs(t)= h(t) * f (t) 。
解
2.4 卷积积分的性质
一、卷积的代数运算
1.交换律
![]()
证明交换律

2.分配律
![]()
与“系统并联运算”有关:

结论:子系统并联时,总系统的冲激响应等于各子系统冲激响应之和。
3.结合律
![]()
与“系统级联运算”有关
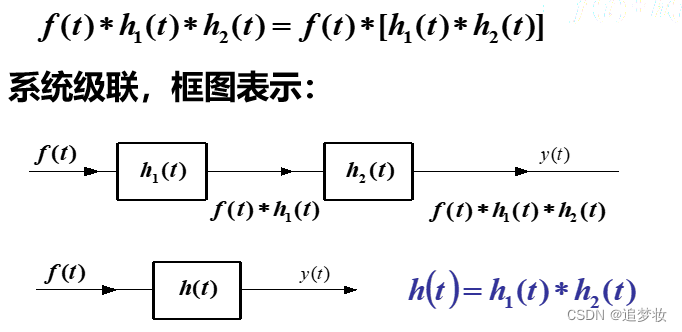
结论:子系统级联时,总的冲激响应等于子系统冲激响应的卷积。
二、函数与冲激函数的卷积
概括

卷积的时移特性
介绍
若 f(t) = f1(t)* f2(t),
则 f1(t –t1)* f2(t –t2) = f1(t –t1 –t2)* f2(t)
= f1(t)* f2(t –t1 –t2)
= f(t –t1 –t2)
卷积性质例
例 f1(t), f2(t)如图,求f1(t)* f2(t)
解 f1(t) = 2ε (t) –2ε (t –1) f2(t) = ε (t+1) –ε (t –1)
f1(t)* f2(t) = 2 ε (t)* ε (t+1) –2 ε (t)* ε (t –1) –2ε (t –1)* ε (t+1) +2ε (t –1)* ε (t –1)
由于ε (t)* ε (t) = tε (t)
据时移特性,有 f1(t)* f2(t) = 2 (t+1) ε (t+1) - 2 (t –1) ε (t –1)–2 tε (t) +2 (t –2) ε (t –2)
三、卷积的微分与积分
概括

卷积性质例
例 f1(t) 如图
, f2(t) = e–tε(t),求f1(t)* f2(t)
解
卷积性质例
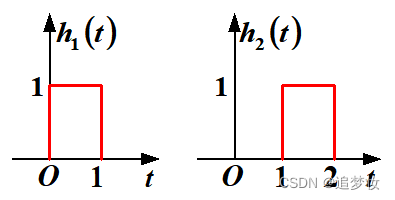
例 图(a)系统由三个子系统构成,已知各子系统的冲激响应h1(t),h2(t)如图(b)所示。求复合系统的冲激响应h(t),并画出它的波形。
图(a)
图(b)解
综合
当激励无冲激函数的导数时,可定性判断,定量分析
当激励有冲激函数的导数时,可使用系数匹配法或借助简单系统
求解步骤
求齐次解:根据方程与特征方程求得已知特征根和未知系数
求特解:根据f(t)与特征根设y(t),代入方程求y(t)
求全解:根据0+和0-代入方程得出系数
求解卷积的方法可归纳为
(1)利用定义式,直接进行积分。对于容易求积分的函数比较有效。如指数函数,多项式函数等。
(2)图解法。特别适用于求某时刻点上的卷积值。
(3)利用性质。比较灵活。三者常常结合起来使用。