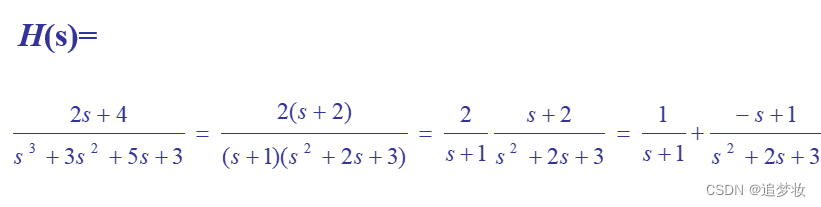连续信号时域描述

考虑欧拉公式：正弦信号可以描述为
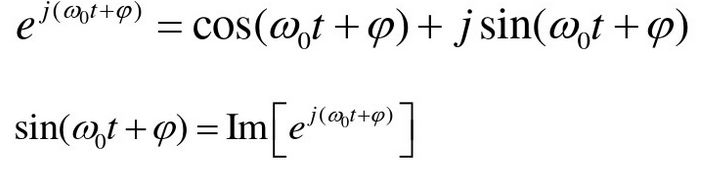要想让叠加的正弦信号也是周期的需要满足：k1T1=k2T2，合成周期为两周期的最小公倍数。

冲激信号的描述：
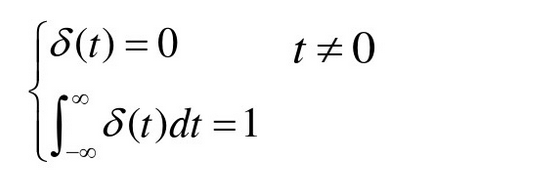它的性质包括：筛选、尺度变换、卷积
冲激偶

时间尺度变换：
表现为函数图的展扩或压缩

翻转：将信号进行对称映射
平移：“左增右减”
卷积：

周期信号的傅里叶级数

非周期信号的傅里叶变换：

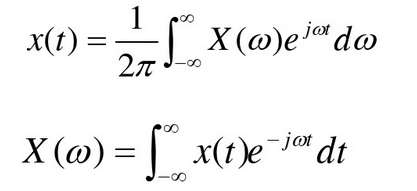
常用非周期信号的傅里叶变换对

非周期信号傅里叶变换性质：

连续信号的复频域

拉普拉斯变换：
在拉普拉斯变换中要涉及到变换收敛域的问题。
收敛域一般可以根据极点来确定，如：

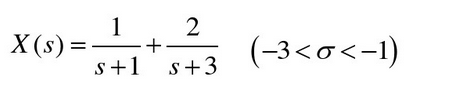
采样和恢复

由抽样信号恢复原连续信号

离散信号的时域分析

离散周期傅里叶级数 频谱分析（DFS）：
离散非周期傅里叶级数（DTFT）：
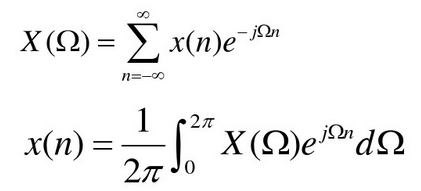DTFT性质：
离散傅里叶变换（DFT）：

增长型的离散信号的傅里叶变换不收敛，为了满足傅里叶变换的条件需要将DFT中的系数乘一个实指数信号r^(-n),从而使其满足收敛条件。

FFT

FFT是一种DFT的高效算法，称为快速傅立叶变换（fast Fourier transform）。FFT算法可分为按时间抽取算法和按频率抽取算法，先简要介绍FFT的基本原理。改进DFT算法，减小它的运算量，利用DFT中算子的周期性和对称性，使整个DFT的计算变成一系列迭代运算，可大幅度提高运算过程和运算量，这就是FFT的基本思想。（后续需要再具体学习）