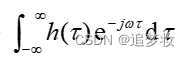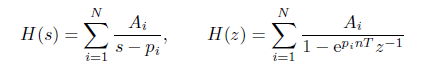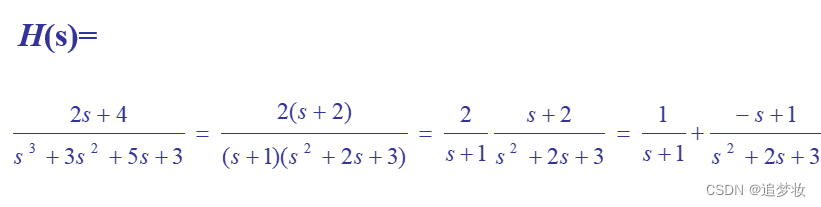信号与系统复习概括

article/2025/9/29 5:57:20

本文是针对自己信号与系统理解不够透彻的一些知识点的梳理，仅供自己学习使用，内容可能有些杂乱。

一、信号与系统总体描述

Q1:信号与系统这门课程讲了什么？

主要从输入-输出描述法出发，研究确定性信号经线性时不变系统，会产生什么响应。

归根到底是研究为了特定的需求设计系统函数。

分析的方法是将一个复杂信号分解为若干个简单信号的叠加。

信号与系统是后续数字信号处理、通信原理等课程的基础课，所以它的作用不容小觑，它可以使原来在时域不好分析的随机信号转换为变换域方便分析，使离散的信号转换为z域进行性质分析，并将信号分解成多个信号进行分析，研究其幅度和相位的性质，剩下一些细节就是计算方面的了。

Q2：系统的数学模型（常用器件）

连续系统：积分器、加法器、数乘器、延时器

离散系统：延迟单元、加法器、数乘器

Q3：线性时不变系统性质

线性（齐次性+可加性）+时不变性-----------------利用常系数线性微分方程描述

因果性、稳定性

那如何判断系统稳定性嘞？（系统在平衡状态下受到扰动时，经过“足够长”的时间以后，系统恢复到平衡状态的能力。系统的稳定性是相对于系统的平衡状态而言的。）

时域：零状态响应是有界的，即系统为有界输入有界输出系统（BIBO）

复频域：

Q4：线性时不变系统的一些数学运算

卷积：LTI系统的零状态响应是激励与冲激响应的卷积积分。 反卷积：FCN于反卷积(Deconvolution)、上采样(UpSampling)_skyfengye的博客-CSDN博客_反卷积上采样具体可参考这个文章

相关函数：

均值和方差只刻画随机过程X（t）在各个独立时刻的概率统计特性，反映不了随机过程的内在相关性，所以引入了自相关函数。通过这种分析，可以分析出信号中的噪声并加以去除；或者从畸变的波形中分离出基波和谐波等。可以将时移前后的信号当成两个信号分析。

Q5：正弦序列是否周期的判定原理

正弦序列： $f(k) = Acos(\Omega _{0}k+\varphi )$

须满足条件 $\frac{2\pi }{\Omega _{0}}=\frac{N}{M}$ 为有理数时，正弦序列是周期序列。Why?如果正弦序列是抽样得到的，采样时间间隔为Ts，则： $f(k)=cos(\omega _{0}t)|_{t=kT_{s}}=cos(\frac{2\pi }{T_{0}}\times kT_{s})$ =cos(Ω0*k),所以由于T0为2*pi的整数倍所以 $\frac{2\pi }{\Omega _{0}}=\frac{N}{M}$ 时两个周期的比值才可以为有理数，即几个采样周期之后与 cos（）=0重合。