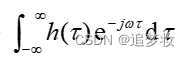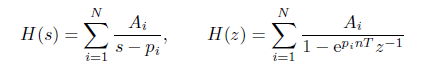文章目录
- 第一章 信号与系统概述
- 1.1 信号的基本概念与分类
- 1.1.1 消息、信息、信号
- 1.1.2 信号的描述
- 1.1.3 信号的分类
- 1.1.3.1 确定信号和随机信号
- 1.1.3.2 连续信号和离散信号
- 1.1.3.3 周期信号与非周期信号
- 1.1.3.4 能量信号和功率信号
- 1.1.3.5 因果信号和反因果信号
- 1.1.3.6 一维信号与二维信号
第一章 信号与系统概述
1.1 信号的基本概念与分类
1.1.1 消息、信息、信号
消息(message):人们常常把来自外界的各种报道统称为消息。接受到某个消息,会引起接收者的知识状态发生改变。知识状态改变的程度由该消息中所包含的信息量决定。
信息(information):是信息论的一个术语,通常把消息中有意义的内容称为信息。某事件发生的信息量可定义为
I = − l o g a P ( x ) I=-log_aP(x) I=−logaP(x)
其中 P ( x ) P(x) P(x)为事件 x x x的概率,当取2为底的对数时,信息量的单位为bit。
信号(signal):信号是信息的载体。如上课铃响的声信号,十字路口的红绿灯是光信号,电视机天线接收的电视信息是电信号。日常生活中的文字信号、图像信号、生物电信号等,都是信号。
为了有效地传播和利用信息,常常需要将信号转换成便于传输和处理的电信号。例如,无线广播就是将语音信号变换为适宜远距离传播的载波信号(这个过程称为调制),由天线发射出去;收音机通过无线接收到信号,通过信号变换形成语音信号(这个过程称为解调)
1.1.2 信号的描述
信号的携带信息的独立变量的函数。信号的信息的一种物理体现,一般是随时间或位置变换的物理量。电信号的基本形式是随时间变化的电压或电流。
描述信号的常用方法:
- 表示为时间的函数
- 信号的图形表示——波形
"信号"与"函数"通常相同通用
1.1.3 信号的分类
1.1.3.1 确定信号和随机信号
- 确定信号:可用确定时间函数表示的信号。

- 随机信号:信号不能用确切的函数描述,只可能知道它的统计特性比如概率,例如:电子系统中的起伏热噪声、雷电干扰信号。 (注意:下图是发生以后记录下来的,每一个时刻是什么值是不确定的)

1.1.3.2 连续信号和离散信号
- 连续时间信号:连续时间范围内( − ∞ < t < ∞ -∞<t<∞ −∞<t<∞)有定义的信号,简称
连续信号;若其函数值域也连续,常称为模拟信号。
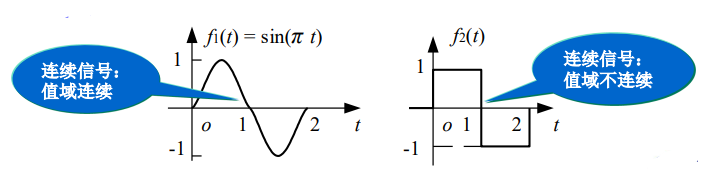
- 离散时间信号:仅在一些离散的瞬间才有定义的信号,简称
离散信号;当取值为规定数值时,常称为数字信号。
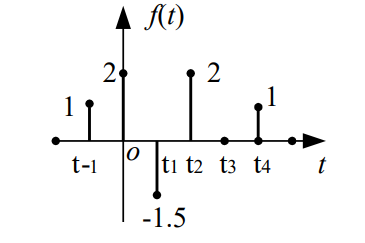
f ( t ) f(t) f(t)仅在一些离散时刻 t k ( k = 0 , ± 1 , ± 2 , … ) t_k(k=0,±1,±2,…) tk(k=0,±1,±2,…)有定义,其余时间无定义,如图:
相邻离散点的间隔 T k = t k + 1 − t k T_k=t_{k+1}-t_k Tk=tk+1−tk通常取等间隔 T T T,离散信号可表示为 f ( k T ) f(kT) f(kT),简写为 f ( k ) f(k) f(k),如果等间隔,这种离散信号也常称为离散序列或序列。其中 k k k称为序号,如图:
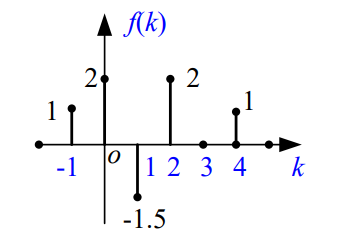

通常将对应某序号 m m m的序列值称为第 m m m个样点的样值。
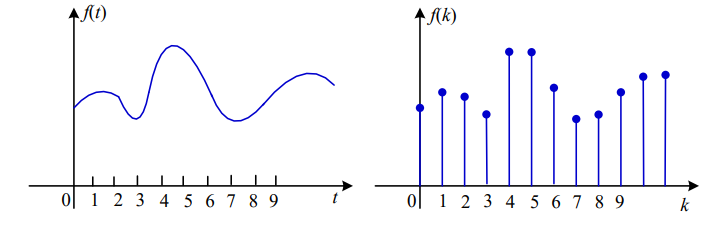
连续信号采样变离散信号:
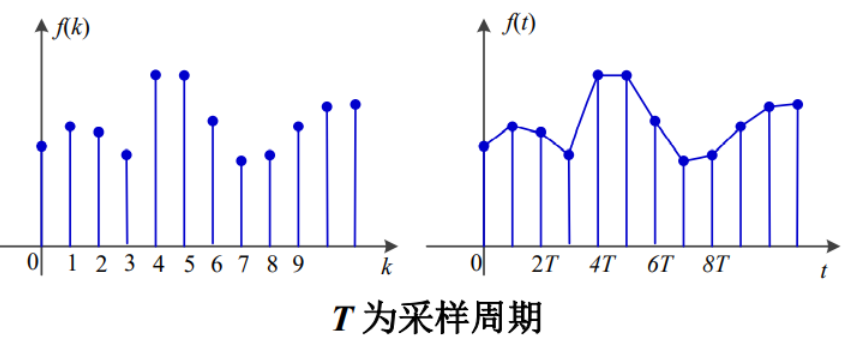
离散信号变连续信号(零阶保持):

离散信号变连续信号(分段线性):
1.1.3.3 周期信号与非周期信号
-
周期信号(period signal)是定义在 ( − ∞ , ∞ ) (-∞,∞) (−∞,∞)区间,每隔一定时间 T T T (或整数 N N N ),按相同规律重复变化的信号; -
不具有周期性的信号称为
非周期信号。
连续信号的周期
连续周期信号 f ( t ) f(t) f(t),周期为 T T T,满足
f ( t ) = f ( t + m T ) , m = 0 , ± 1 , ± 2 , … f(t) = f(t + mT),m = 0,±1,±2,… f(t)=f(t+mT),m=0,±1,±2,…
典型周期连续信号:余弦信号 cos ω t \text{cos}ωt cosωt
周期为: T = 2 π / ω ( s ) T= 2π/ω (s) T=2π/ω(s)
两个周期信号的周期分别为 T 1 T_1 T1和 T 2 T_2 T2,若 T 1 / T 2 T_1/T_2 T1/T2为有理数,则周期信号之和仍然是周期信号,其周期为 T 1 T_1 T1和 T 2 T_2 T2的最小公倍数。


离散信号的周期
定义:离散周期信号 f ( k ) f(k) f(k),周期为 N N N,满足下式:
f ( k ) = f ( k + m N ) , m = 0 , ± 1 , ± 2 , … f(k) = f(k + mN),m = 0,±1,±2,… f(k)=f(k+mN),m=0,±1,±2,…

结论:
- 当 2 π / β 2π/β 2π/β为整数时,正弦序列具有周期 N = 2 π / β N = 2π/β N=2π/β;
- 当 2 π / β 2π/β 2π/β为有理数时,正弦序列仍具有周期性,但其周期为 N = M ( 2 π / β ) N= M(2π/β) N=M(2π/β), M M M取使 N N N为整数的最小整数;
- 当 2 π / β 2π/β 2π/β为无理数时,正弦序列为非周期序列。

结论:
- ①连续正弦信号一定是周期信号,而正弦序列不一定是周期序列。
- ②两连续周期信号之和不一定是周期信号,而两周期序列之和一定是周期序列。
1.1.3.4 能量信号和功率信号
将信号 f ( t ) f(t) f(t)看作电压信号或电流信号, 施加于 R = 1 Ω R=1Ω R=1Ω电阻上,它所消耗的瞬时功率为 ∣ f ( t ) ∣ 2 | f(t) |^2 ∣f(t)∣2( P = ∣ u ( t ) ∣ 2 R = ∣ f ( t ) ∣ 2 P=\frac{|u(t)|^2}{R}=|f(t)|^2 P=R∣u(t)∣2=∣f(t)∣2,考虑到 u ( t ) u(t) u(t)可能是复数,所以取模。),在区间 ( – ∞ , ∞ ) (–∞ , ∞) (–∞,∞)的能量和平均功率(单位时间消耗的能量为功率)定义为:

能量有限信号: 信号的能量 E < ∞ E<∞ E<∞,简称能量信号,此时 P = 0 P = 0 P=0。
功率有限信号: 信号的功率 P < ∞ P<∞ P<∞,简称功率信号,此时 E = ∞ E = ∞ E=∞。
对于离散信号,也有能量信号、功率信号之分。
能量信号:满足 E = ∑ k = − ∞ ∞ ∣ f ( k ) ∣ 2 < ∞ E=\sum_{k=-\infty}^{\infty}|f(k)|^{2}<\infty E=∑k=−∞∞∣f(k)∣2<∞的离散信号
功率信号:满足 P = lim N → ∞ 1 N ∑ k = − N / 2 N / 2 ∣ f ( k ) ∣ 2 < ∞ P=\lim _{N \rightarrow \infty} \frac{1}{N} \sum_{k=-N / 2}^{N / 2}|f(k)|^{2}<\infty P=limN→∞N1∑k=−N/2N/2∣f(k)∣2<∞的离散信号
结论:
(1) 时限信号(仅在有限时间区间不为零)为能量信号;
(2) 周期信号属于功率信号;
(3) 非周期信号可能是能量信号,也可能是功率信号;
(4) 有些信号既不是能量信号也不是功率信号,如 f ( t ) = e t f(t)=e^t f(t)=et
1.1.3.5 因果信号和反因果信号
- 因果信号: t < 0 , f ( t ) = 0 t < 0,f(t)=0 t<0,f(t)=0的信号 f ( t ) f(t) f(t) [即 t = 0 t=0 t=0 时接入系统的信号],比如阶跃信号:

- 反因果信号(备注:不是非因果信号): t ≥ 0 t ≥ 0 t≥0, f ( t ) = 0 f(t)=0 f(t)=0的信号 (除0信号外)。
1.1.3.6 一维信号与二维信号
从数学表达式看,信号可以表示为一个或多个变量的函数,分别称为一维或多维信号(函数)。
语音信号可表示为声压随时间变化的函数,属于一维信号。而一张黑白图像每个点(像素)具有不同的光强度,任一点又是二维平面坐标中两个变量的函数,黑白图像属于二维信号。还有更多维变量的函数的信号。
还有其他分类,如实信号与复信号;左边信号与右边信号等等。
《工程信号与系统》作者:郭宝龙等
国家精品课程:信号与系统 ,中国大学MOOC,郭宝龙,朱娟娟