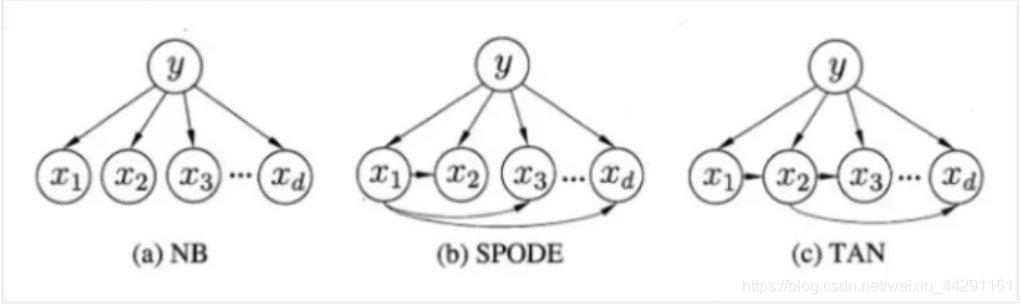
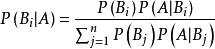贝叶斯的思想比较简单,网上阐述也很详细,这里就不赘述了。
这里只是简单的说一下编程的思路
首先明确我们要实验的内容,实现贝叶斯分类,那么要想编程实现,你必须对贝叶斯分类有足够的了解。而贝叶斯分类的过程并不难,总的来说就是,有了一些训练数据,当来了一条测试数据,首先根据训练数据计算先验概率,比如有17条训练数据,8条好瓜,9条坏瓜,那么P(好瓜) = 8 / 17,坏瓜以此类推。
紧接着计算后验概率,比如测试数据第一个属性是色泽,值为青绿,那么就计算训练数据中所有好瓜里面色泽为青绿的个数,比如有3个,那么得到P(青绿 | 好瓜) = 3 / 8,以此类推计算所有属性,那么比如测试数据有5个属性,而数据有两个类别,那么一共要计算10个概率。
最后将P(好瓜) * P(青绿 | 好瓜) * … * = P1
P(坏瓜) * P(青绿 | 坏瓜) * … * = P2
比较P1P1谁大,测试是数据就是哪个类别。
-
伪代码
Class BayesClassifier():
1、 初始化,# 参数可以自己添加
即让训练集为空
2、 Fit
其实就是输入训练集
3、 计算先验概率
4、 计算后验概率(难点)
5、 预测
输入一条测试数据,给出预测结果
6、 评估
输入一组测试数据(即测试集),返回测试精度 -
思路
我打算用sklearn的train_test_split来划分数据集。那么现在还要想明白的就是,将数据文件导入后,用什么数据类型便于计算呢?先验概率好求,后验概率怎么编程实现呢?在后续的编写中,我发现难点其实在于,你划分了数据集,X_train的样子大概是这样:

而y_train的样子是这样:

那么问题来了,在计算后验概率的时候,你要如何将类别为好瓜的位置找出来呢?为什么要找?比如第一个属性,找出来才能计算好瓜中青绿的个数呀,找出来以后用什么存放呢?字典呀!我可以在计算先验概率时先算出好瓜的个数,坏瓜的个数,放到一个字典里面like:{‘好瓜’:4,’坏瓜’:8},接着因为y_train和X_train的索引是一一对应的,那么我就可以根据y_train得出好瓜的位置呀!like: {‘好瓜’:[3,5,7],’坏瓜’:[0,1,2,4,6]},再根据这个位置去找X_train统计青绿的个数。
统计完个数就可以计算后验概率了,like:{‘坏瓜’:[0.3,0.375,0.126,0.45],’好瓜’:[0.6,0.2,0.5,0.6]},这里我特地不加以区分的直接把所有概率放进一个列表里,为什么这么做呢?因为后面用到的时候只是把所有都乘起来即可,无需加以区分。
还需要注意的就是,对离散值和连续值的处理,离散值就是上面的方法,连续值就是需要先算出训练集该属性的均值和标准差接着用下面的公式: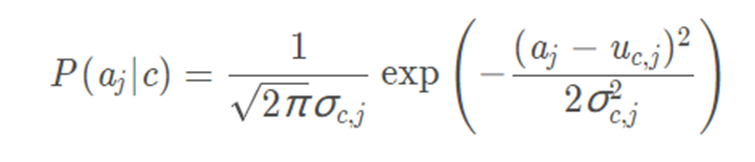
计算即可,还有就是在计算之前判断一下是离散值还是连续值即可,一个if ,else就能解决的问题。
事实上如果编程实现了上面的步骤,拉普拉斯修正就是加几句代码的问题。
BayesClassifier.py
# -*- coding: utf-8 -*-"""
Created on Tue Apr 21 10:53:41 2020@author: Hja
@Company:北京师范大学珠海分校
@version: V1.0
@contact: 583082258@qq.com 2018--2020
@software: Spyder
@file: BayesClassifier.py
@time: 2020/4/22 9:02
@Desc:贝叶斯分类器
@PS : 将贝叶斯分类器封装起来
"""import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings("ignore")#消除警告class Bayes_Classifier(object):'''贝叶斯分类器'''def __init__(self):'''定义训练集'''self.X_train = Noneself.y_train = Nonedef fit(self,X_train,y_train):# 给训练集赋值'''X_train is array ,shape like [n_samples,shapes]X_train is array ,shape like [n_samples,1]'''self.X_train = X_trainself.y_train = y_traindef cal_base_rates(self):'''计算先验概率data为训练集'''#存放先验概率,如{'好瓜':0.471}cal_base_rates = {}#首先查看数据一共有几个决策属性labels = self.Get_Decision_attribute()#计算先验概率for label in labels:#如 : '是'在y_train_data中出现的次数 / 在y_train_data的长度priori_prob = sum(self.y_train == label) / len(self.y_train)#放入字典中cal_base_rates[label] = priori_probreturn cal_base_ratesdef Get_Decision_attribute(self):'''获得数据集的决策属性'''labels = set(self.y_train)return labelsdef Conditional_Probability(self,X_test):'''为每个属性估计条件概率,data为待预测数据return {'好瓜':{'青绿': 0.375}}X_train_data,y_train_data为训练集X_test like:['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.46]'''labels = self.Get_Decision_attribute()#统计不同类别的个数,如{'好' : 3,'坏':8}labels_count = {}#存放好瓜,坏瓜的编号,like :{’好': [[2],[4],[10]],'坏' : [...]}labels_place = {}# 存放后验概率cal_base_rates = {}for label in labels:labels_count[label] = sum(self.y_train == label)#记录好瓜,坏瓜的编号labels_place[label] = np.argwhere(self.y_train == label)cal_base_rates[label] = []# 初始化flag = 0#计算每个属性的条件概率for value in X_test:#对连续值的处理if type(value) != str:for label,places in labels_place.items():#int_value = []#如:存放好瓜的密度for place in places:int_value.append(self.X_train[place,flag])#将取值放入,方便等会计算均值,标准差# 计算均值,标准差value_mean = np.mean(int_value)value_std = np.std(int_value)#高斯模型race = (np.exp(((value - value_mean) ** 2) / (-2 * (value_std ** 2)))) / (np.sqrt(2 * np.pi) * value_std)cal_base_rates[label].append(race)# 对离散值的处理else:for label,places in labels_place.items():#value_count = 0# 用来统计某个元素的个数: 如'青绿' 3 次,那么value_count = 3for place in places:if value == self.X_train[place,flag]:value_count += 1#计算概率race = value_count / len(places) #places的个数即好瓜的个数 or 坏瓜# 这里不加标记是那个取值的概率,是因为后面都是直接乘积cal_base_rates[label].append(race)# like: {'好' :[0.357,0.625,...]}flag = flag + 1return cal_base_ratesdef Predict(self,X_test):'''给出一条数据的预测结果,X_test like:['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.46] '''from functools import reduce# 得出先验概率和后验概率result_behind = self.Conditional_Probability(X_test)result_before = self.cal_base_rates()# 计算概率max_race = 0flag = Nonefor label,value in result_behind.items():race = reduce(lambda x,y:x * y,value) * result_before[label] # 计算概率if max_race < race: max_race = raceflag = labelreturn flag # 返回类别def Score_model(self,X_test,y_test):'''返回测试集精度给出一组数据的精度结果,X_test like:['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', 0.639, 0.161],['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.6970000000000001, 0.46],['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', 0.608, 0.318]......'''y_pred = []for item in X_test:result = self.Predict(item)y_pred.append(result)return np.mean(y_pred == y_test)# 考虑到该模型精度波动大,我们做十次去均值
def Mean_of_model(data,cv = 10):'''data为数据集'''score = []for i in range(cv):X_train,X_test,y_train,y_test = train_test_split(data[:,:-1],data[:,-1],test_size = 0.3)score.append(Score_model(X_train,y_train,X_test,y_test))return np.mean(score)if __name__ == '__main__':#设置数据文件路径path = r'F:\大三下\李艳老师数据挖掘实践\实验五\西瓜数据.csv'#读取文件data = pd.read_csv(path)data.drop(columns = '编号',inplace = True)#转换为array类型,便于计算data_np = np.array(data)#插看前五行#print(data_np[:5,:])#色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜#划分数据,data_np[:,-1]为决策属性列X_train,X_test,y_train,y_test = train_test_split(data_np[:,:-1],data_np[:,-1],\test_size = 0.3)#test = np.array(['青绿','蜷缩','浊响','清晰','凹陷','硬滑',0.697,0.460])test = ['青绿','蜷缩','浊响','清晰','凹陷','硬滑',0.697,0.460]# 建立模型bayes = Bayes_Classifier()# 训练模型bayes.fit(X_train,y_train)# 给出对test的预测结果y_pred = bayes.Predict(test)print("{} 的分类结果 {} 好瓜".format(test,y_pred))#print(y_pred)# 查看后验概率#print(bayes.Conditional_Probability(test))# 打印测试集精度print("Test set score: {:.2f}".format(bayes.Score_model(X_test,y_test)))# 用全部数据作为训练集,看得出的结果与PPT的是否相同,证明是相同的bayes.fit(data_np[:,:-1],data_np[:,-1])y_pred = bayes.Predict(test)# 从结果可以看出,p(青绿|好瓜) = 0.375,p(青绿|坏瓜) = 0.333...print("后验概率:",bayes.Conditional_Probability(test))print("先验概率:",bayes.cal_base_rates())#print("{} 的分类结果 {} 好瓜".format(test,y_pred))# 用十次留出法的均值来评估模型cv = 50scores = []for i in range(cv):X_train,X_test,y_train,y_test = train_test_split(data_np[:,:-1],data_np[:,-1],\test_size = 0.3)bayes = Bayes_Classifier()bayes.fit(X_train,y_train)# print("Test set score: {:.2f}".format(bayes.Score_model(X_test,y_test)))scores.append(bayes.Score_model(X_test,y_test))#print("用{}次留出法的均值来评估模型 :{:.2f}".format(cv,np.mean(scores)))# 画图import matplotlib.pyplot as plt# 不同的划分对模型的影响plt.figure(figsize = (4,4),dpi = 144)plt.grid()plt.plot(range(cv),scores,'g-')plt.xlabel('Differernt Divide')plt.ylabel('Score')plt.title('Influence of different Divide on accuracy')plt.show()- 结果分析
我首先使用一条数据去测试,即

test = ['青绿','蜷缩','浊响','清晰','凹陷','硬滑',0.697,0.460]
# 建立模型
bayes = Bayes_Classifier()
# 训练模型
bayes.fit(X_train,y_train)
y_pred = bayes.Predict(test)
print("{} 的分类结果 {} 好瓜".format(test,y_pred))
Out:
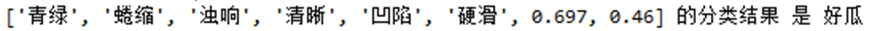
如果你仔细看过代码,可以发现,bayes.Predict是针对一条数据进行预测的,而bayes.Score_model的输入是测试集,即遍历每一条数据,将每一条数据代入bayes.Predict进行计算。
为了验证程序的正确性,我将所有数据作为训练集,单独测试下面的数据,看下计算出来的概率和PPT中的是否相同。
test = [‘青绿’,‘蜷缩’,‘浊响’,‘清晰’,‘凹陷’,‘硬滑’,0.697,0.460]
# 用全部数据作为训练集,看得出的结果与PPT的是否相同,证明是相同的
bayes.fit(data_np[:,:-1],data_np[:,-1])
y_pred = bayes.Predict(test)
# 从结果可以看出,p(青绿|好瓜) = 0.375,p(青绿|坏瓜) = 0.333...
print("后验概率:",bayes.Conditional_Probability(test))
print("先验概率:",bayes.cal_base_rates())
Out:

该结果中,如“否”:[0.3333333333333333, 0.3333333333333333, 0.4444444444444444, 0.2222222222222222, 0.2222222222222222, 0.6666666666666666, 1.194154974103892, 0.042477456013491184],那么第一个值0.333即为P(青绿|坏瓜) = 0.33,第三个0.44即
P(浊响|坏瓜) = 0.44,显然与PPT计算的一致。

考虑到用该数据集训练的模型波动比较大,我想找出该模型测试集的均值大概是多少,于是我使用100次划分的数据去训练模型,将得到的精度取均值。
并将结果可视化
# 用cv次留出法的均值来评估模型
cv = 100
scores = []
for i in range(cv):
X_train,X_test,y_train,y_test = train_test_split(data_np[:,:-1],data_np[:,-1],\test_size = 0.3)
bayes = Bayes_Classifier()
bayes.fit(X_train,y_train)
# print("Test set score: {:.2f}".format(bayes.Score_model(X_test,y_test)))
scores.append(bayes.Score_model(X_test,y_test))print("用{}次留出法的均值来评估模型 :{:.2f}".format(cv,np.mean(scores)))# 画图
import matplotlib.pyplot as plt
# 不同的划分对模型的影响
plt.figure(figsize = (4,4),dpi = 144)
plt.grid()
plt.plot(range(cv),scores,'g-')
plt.xlabel('Differernt Divide')
plt.ylabel('Score')
plt.title('Influence of different Divide on accuracy')
plt.show()
Out:

从结果可以看出,对于该数据训练出来的模型,泛化能力并不是特别好,对于测试集的精度只在0.5左右。
- 后续
最后:至于拉普拉斯修正嘛,很简单在源程序计算先验概率中修改红字部分

该步对应以下步骤
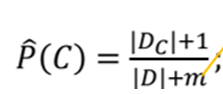

该步实现以下的步骤
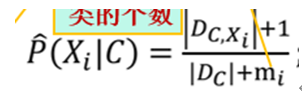
修改以后看看精度有无提升:

可以看到拉普拉斯修正对模型的确实有一定的改正能力。
程序用到的数据集已上传百度云,需要的朋友自行下载
链接:https://pan.baidu.com/s/1ujtT2YsAbHNOm2mbCRNUiA
提取码:q911